Article contents
A note on the queueing system GI/Ek/1
Published online by Cambridge University Press: 14 July 2016
Extract
In this note we adopt the notation and terminology of Kingman (1966) without further comment. For the general single server queue one has
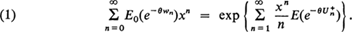 For the queueing system GI/Ek/1 it is possible to make use of the particular nature of the service time distribution to evaluate the right-hand side of Equation (1) in terms of the k roots of a certain equation. This evaluation is carried out in detail in Prabhu (1965) to which reference should be made for the technicalities involved. A similar evaluation applies to the limiting distribution
For the queueing system GI/Ek/1 it is possible to make use of the particular nature of the service time distribution to evaluate the right-hand side of Equation (1) in terms of the k roots of a certain equation. This evaluation is carried out in detail in Prabhu (1965) to which reference should be made for the technicalities involved. A similar evaluation applies to the limiting distribution
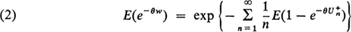 when it exists. However, the resulting expression again involves the k roots of a certain equation. In this note we draw attention to an alternative procedure which does not involve the calculation of roots. We remark that a similar, but slightly different, procedure can be used in the study of the queueing system Ek/GI/1. Details of this will be presented in a separate note.
when it exists. However, the resulting expression again involves the k roots of a certain equation. In this note we draw attention to an alternative procedure which does not involve the calculation of roots. We remark that a similar, but slightly different, procedure can be used in the study of the queueing system Ek/GI/1. Details of this will be presented in a separate note.
- Type
- Short Communications
- Information
- Copyright
- Copyright © Applied Probability Trust
References
- 6
- Cited by


