Published online by Cambridge University Press: 14 July 2016
The asymptotic distribution of the traffic average in the case of M/G/∞ with bulk arrivals has been proved in [7] to be normal with mean μCμPμF and variance 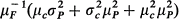 where
where 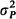 and
and 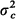 are the variances and μP and μc are the means of the service-time and the batch-size respectively, μF being the mean inter-arrival time. We prove in this note that the asymptotic normality holds even in the more general case of a G//G/∞ with bulk arrivals.
are the variances and μP and μc are the means of the service-time and the batch-size respectively, μF being the mean inter-arrival time. We prove in this note that the asymptotic normality holds even in the more general case of a G//G/∞ with bulk arrivals.