Hostname: page-component-5cf477f64f-bmd9x Total loading time: 0 Render date: 2025-04-08T05:26:27.405Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Branching Random Walks on Finite Sets

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

Thomas Mountford  and
Rinaldo B. Schinazi
Thomas Mountford*
Affiliation:
EPFL-DMA
Rinaldo B. Schinazi*
Affiliation:
University of Colorado
*
∗Postal address: EPFL-DMA, CH-1015 Lausanne, Switzerland. Email address: [email protected]
∗∗Postal address: Department of Mathematics, University of Colorado, Colorado Springs, CO 80933, USA. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that a branching random walk that is supercritical on 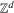is also supercritical, in a rather strong sense, when restricted to a large enough finite ball of 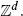This implies that the critical value of branching random walks on finite balls converges to the critical value of branching random walks on 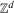as the radius increases to infinity. Our main result also implies coexistence of an arbitrary finite number of species for an ecological model.

Keywords

Branching random walkcoexistenceecological modelspatial stochastic modelcontact process

MSC classification

Secondary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Short Communications
Information
Journal of Applied Probability , Volume 42 , Issue 1 , March 2005 , pp. 287 - 294
Copyright
© Applied Probability Trust 2005 

References

Aldous, D. and Fill, J. (2003). Reversible Markov chains and random walks on graphs. Work in progress. Drafts of chapters available at http://www.stat.berkeley.edu/users/aldous/.Google Scholar
Engländer, J. and Kyprianou, A. E. (2004). Local extinction versus local exponential growth for spatial branching processes. Ann. Prob. 32, 78–99.Google Scholar
Engländer, J. and Pinsky, R. G. (1999). On the construction and support properties of measure-valued diffusions on D {R}d with spatially dependent branching. Ann. Prob. 27, 684–730.CrossRefGoogle Scholar
Ethier, S. N. and Kurtz, T. G. (1986). Markov Processes. Characterization and Convergence. John Wiley, New York.CrossRefGoogle Scholar
Itô, K. and McKean, H. P. (1965). Diffusion Processes and Their Sample Paths. Springer, Berlin.Google Scholar
Kesten, H. and van den Berg, J. (2000). Asymptotic density in a coalescing random walk model. Ann. Prob. 28, 303–352.CrossRefGoogle Scholar
Liggett, T. M. (1985). Interacting Particle Systems, Springer, New York.Google Scholar
Liggett, T. M. (1999). Branching random walks on finite trees. In Perplexing Problems in Probability (Progress Prob. 44), eds Bramson, M. and Durrett, R., Birkhäuser, Boston, MA, pp. 315–330.Google Scholar
Neuhauser, C. (1992). Ergodic theorems for the multitype contact process. Prob. Theory Relat. Fields 91, 467–506.Google Scholar
Pemantle, R. and Stacey, A. M. (2001). The branching random walk and contact process on Galton–Watson and nonhomogeneous trees. Ann. Prob. 29, 1563–1590.CrossRefGoogle Scholar