Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2025-01-03T20:57:33.112Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on a functional equation arising in Galton-Watson branching processes

Published online by Cambridge University Press:  14 July 2016

Krishna B. Athreya
Krishna B. Athreya*
Affiliation:
University of Wisconsin
Get access Rights & Permissions [Opens in a new window]

Abstract

The functional equation ϕ(mu) = h(ϕ(u)) where 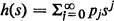is a probability generating function with 1 < m = h'(1 –) < ∞ and 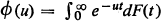where F(t) is a non-decreasing right continuous function with F(0 –) = 0, F(0 +) < 1 and F(+ ∞) = 1 arises in a Galton-Watson process in a natural way. We prove here that for any 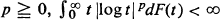if and only if 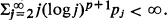This unifies several results in the literature on the supercritical Galton-Watson process. We generalize this to an age dependent branching process case as well.

Type
Research Papers
Information
Journal of Applied Probability , Volume 8 , Issue 3 , September 1971 , pp. 589 - 598
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. B. (1969) On the supercritical one dimensional age dependent branching processes. Ann. Math. Statist. 40, 743–763.CrossRefGoogle Scholar
[2] Kesten, H. and Stigum, B. P. (1966) A limit theorem for multidimensional Galton-Watson processes. Ann. Math. Statist. 37, 1211–1223.Google Scholar
[3] Seneta, E. (1968) On recent theorems concerning the supercritical Galton-Watson process. Ann. Math. Statist. 39, 2098–2102.CrossRefGoogle Scholar
[4] Heathcote, C. R., Seneta, E. and Vere-Jones, D. (1967) A refinement of two theorems in the theory of branching processes. Teor. Veroyat. Primen. 12, 341–346.Google Scholar
[5] Feller, W. (1966) An Introduction to Probability Theory and Its Applications, Vol. II. John Wiley, New York. 272–276 and 418–423.Google Scholar