Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T11:35:37.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-explosivity of limits of conditioned birth and death processes

Part of: Probability theory on algebraic and topological structures Markov processes

Published online by Cambridge University Press:  14 July 2016

G. O. Roberts ,
S. D. Jacka  and
P. K. Pollett
G. O. Roberts*
Affiliation:
University of Cambridge
S. D. Jacka*
Affiliation:
University of Warwick
P. K. Pollett*
Affiliation:
University of Queensland
*
∗Postal address: Statistical Laboratory, 16 Mill Lane, Cambridge CB2 ISB, UK.
∗∗Postal address: Department of Statistics, University of Warwick, Coventry CV4 7AL, UK.
∗∗∗Postal address: Department of Mathematics, University of Queensland, Queensland 4072, Australia.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a birth and death process on 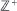with absorption at zero and suppose that X is suitably recurrent, irreducible and non-explosive. In a recent paper, Roberts and Jacka (1994) showed that as T → ∞ the process conditioned to non-absortion until time T converges weakly to a time-homogeneous Markov limit, X∞, which is itself a birth and death process. However the question of the possibility of explosiveness of X∞ remained open. The major result of this paper establishes that X∞ is always non-explosive.

Keywords

INVARIANT MEASURESQUASI-STATIONARY DISTRIBUTIONS

MSC classification

Primary: 60J27: Continuous-time Markov processes on discrete state spaces
Secondary: 60B10: Convergence of probability measures
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 1 , March 1997 , pp. 35 - 45
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Jacka, S. D. and Roberts, G. O. (1995) Weak convergence of conditioned processes on a countable state space. J. Appl. Prob. 32, 902–916.CrossRefGoogle Scholar
Karlin, S. and Mcgregor, J. (1959) A characterization of birth and death processes. Proc. Nat. Acad. Sci. 9, 1141–1164.Google Scholar
Kendall, D. G. (1959) Unitary dilations of one-parameter semigroups of Markov transition operators, and the corresponding integral representations for Markov processes with a countable infinity of states. Proc. London Math. Soc. 9, 417–431.CrossRefGoogle Scholar
Pollett, P. K. (1986) On the equivalence of µ-invariant measures for the minimal process and its q-matrix. Stoch. Proc. Appl. 22, 203–221.CrossRefGoogle Scholar
Pollett, P. K. and Vere-Jones, D. (1992) A note on evanescent processes. Austral. J. Statist. 34, 531–536.CrossRefGoogle Scholar
Roberts, G. O. (1991) A comparison theorem for conditioned Markov processes. J. Appl. Prob. 28, 74–83.CrossRefGoogle Scholar
Roberts, G. O. and Jacka, S. D. (1994) Weak convergence of conditioned birth and death processes. J. Appl. Prob. 31, 90–100.CrossRefGoogle Scholar
Seneta, E. (1981) Non-Negative Matrices and Markov Chains. Springer, Berlin.CrossRefGoogle Scholar
Van Doorn, E. A. (1991) Quasi-stationary distributions and convergence to quasi-stationarity of birth-death processes. Adv. Appl. Prob. 23, 683–700.CrossRefGoogle Scholar