Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-22T11:42:04.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Moments based approximation for the stationary distribution of a random walk in Z+ with an application to the M/GI/1/n queueing system

Part of: Special processes

Published online by Cambridge University Press:  14 July 2016

F. Simonot
F. Simonot*
Affiliation:
Université Henri Poincaré
*
∗Postal address: ESSTIN - Université Henri Poincaré, Nancy 1, Rue J. Lamour, 54500 Vandoeuvre, France. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider an irreducible random walk in Z+ defined by X(m+1) = max(0, X(m) + A(m+1)) with E{A} < 0 and 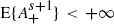for an s ≥ 0 where a+ = max(0,a). Let π be the stationary distribution of X. We show that one can find probability distributions πn supported by {0,n} such that ||πn - π||1 ≤ Cn-s, where the constant C is computable in terms of the moments of A, and also that ||πn - π||1 = o(n-s). Moreover, this upper bound reveals exact for s ≥ 1, in the sense that, for any positive ε, we can find a random walk fulfilling the above assumptions and for which the relation ||πn - π||1 = o(n-s-ε) does not hold. This result is used to derive the exact convergence rate of the time stationary distribution of an M/GI/1/n queueing system to the time stationary distribution of the corresponding M/GI/1 queueing system when n tends to infinity.

Keywords

Markov chainstochastic monotonicity‘skip free left’ matrixrandom walkconvergence rate

MSC classification

Secondary: 60K99: None of the above, but in this section
Type
Short Communications
Information
Journal of Applied Probability , Volume 37 , Issue 1 , March 2000 , pp. 290 - 299
Copyright
Copyright © 2000 by The Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S. (1987). Applied Probability and Queues. John Wiley, New York.Google Scholar
Bhat, N. (1984). Elements of Applied Stochastic Processes, 2nd edn. John Wiley, New York.Google Scholar
Daley, D. J. (1968). Stochastically monotone Markov chains. Z. Wahrscheinlichkeitsth. 10, 305–307.CrossRefGoogle Scholar
Gibson, D., and Seneta, E. (1987). Monotone infinite stochastic matrices and their augmented truncations. Stoch. Proc. Appl. 24, 287–292.CrossRefGoogle Scholar
Gut, A. (1988). Stopped Random Walks—Limit Theorems and Applications. Springer, New York.CrossRefGoogle Scholar
Kalashnikov, V. V. (1994). Mathematical Methods in Queueing Theory. Kluwer, Dordrecht.CrossRefGoogle Scholar
Kalashnikov, V. V., and Rachev, S. T. (1990). Mathematical Methods for Construction of Queueing Models. Wadsworth and Brooks Cole, New York.CrossRefGoogle Scholar
Lindvall, T. (1992). Lectures on the Coupling Method. John Wiley, New York.Google Scholar
Mehdi, J. (1991). Stochastic Models in Queueing Theory. Academic Press, New York.Google Scholar
Simonot, F. (1995). Sur l'approximation de la distribution stationnaire d'une chaine de Markov stochastiquement monotone. Stoch. Proc. Appl. 56, 133–149.CrossRefGoogle Scholar
Simonot, F., and Song, Y. Q. (1996). Characterization of convergence rates for the approximation of the stationary distribution of infinite monotone stochastic matrices. J. Appl. Prob. 33, 974–985.CrossRefGoogle Scholar
Stoyan, D. (1983). Comparison Methods for Queues and Other Stochastic Models. John Wiley, New York.Google Scholar
Tijms, H. C. (1986). Stochastic Modelling and Analysis. John Wiley, New York.Google Scholar