Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T06:44:58.131Z Has data issue: false hasContentIssue false
  • English
  • Français

A method for studying the integral functionals of stochastic processes with applications: I. Markov chain case

Published online by Cambridge University Press:  14 July 2016

Prem S. Puri
Prem S. Puri*
Affiliation:
Purdue University, Lafayette, Indiana
Get access Rights & Permissions [Opens in a new window]

Extract

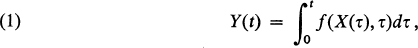The subject of this paper is the study of the distribution of integrals of the type where {X(t); t ≧ 0} is some appropriately defined continuous-time parameter stochastic process, and f is a suitable non-negative function of its arguments. This subject has also sometimes been labelled as “the occupation time or the sojourn time problem” in literature. These integrals arise in several domains of applications such as in the theory of inventories and storage (see Moran [14], Naddor [15]), in the study of the cost of the flow-stopping incident involved in the automobile traffic jams (see Gaver [8], Daley [3], Daley and Jacobs [4]). The author encountered such integrals while studying certain stochastic models suitable for the study of response time distributions arising in various live situations. In fact in [19], it was shown that such a distribution is equivalent to the study of an integral of the type (1). Again, in the study of response of host to injection of virulent bacteria, Y(t) with f(X(t), t) = bX(t), with b > 0, could be regarded as a measure of the total amount of toxins produced by the bacteria during (0, t), assuming a constant toxin-excretion rate per bacterium. Here X(t) denotes the number of live bacteria at time t, the growth of which is governed by a birth and death process (see Puri [16], [17] and [18]).

Type
Research Papers
Information
Journal of Applied Probability , Volume 8 , Issue 2 , June 1971 , pp. 331 - 343
Copyright
Copyright © Applied Probability Trust 1971 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bartlett, M. S. (1961) Equations for stochastic path integrals. Proc. Camb. Phil. Soc. 57, 568–573.CrossRefGoogle Scholar
[2] Chung, K. L. (1967) Markov Chains with Stationary Transition Probabilities. Springer-Verlag, New York.Google Scholar
[3] Daley, D. J. (1969) The total waiting time in a busy period of a stable single-server queue, I. J. Appl. Prob. 6, 550–564.Google Scholar
[4] Daley, D. J. and Jacobs, D. R. Jr. (1969) The total waiting time in a busy period of a stable single-server queue, II. J. Appl. Prob. 6, 565–572.CrossRefGoogle Scholar
[5] Van Dantzig, D. (1948) Sur la méthode des fonctions génératrices. Colloques internationaux du CRNS, 13, 29–45.Google Scholar
[6] Darling, D. A. and Kac, M. (1957) On occupation times for Markoff processes. Trans. Amer. Math. Soc. 84, 444–458.Google Scholar
[7] Feller, W (1966) An Introduction to Probability Theory and its Applications, Vol. II. Wiley, New York.Google Scholar
[8] Gaver, D. P. (1969) Highway delays resulting from flow-stopping incidents. J. Appl. Prob. 6, 137–153.Google Scholar
[9] Karlin, S. and Mcgregor, J. (1961) Occupation time laws for birth and death processes. Proc. 4th Berkeley Symp. Math. Statist. Prob. 2, 249–272.Google Scholar
[10] Kemperman, H. H. B. (1961) The Passage Problem for a Stationary Markov Chain. University of Chicago Press.Google Scholar
[11] Kesten, H. (1962) Occupation times for Markov and semi-Markov processes. Trans. Amer. Math. Soc. 103, 82–112.Google Scholar
[12] Mclean, R. A. and Neuts, M. F. (1967) The integral of a step function defined on a semi-Markov process. SIAM J. Appl. Math. 15, 726–738.Google Scholar
[13] Mcneil, D. R. (1970) Integral functionals of birth and death processes and related limiting distributions. Ann. Math. Statist. 41, 480–485.CrossRefGoogle Scholar
[14] Moran, P. A. P. (1959) The Theory of Storage. Methuen, London.Google Scholar
[15] Naddor, E. (1966) Inventory Systems. Wiley, New York.Google Scholar
[16] Puri, P. S. (1967) A class of stochastic models of response after infection in the absence of defense mechanism. Proc. 5th Berkeley Symp. Math. Statist. Prob. 4, 511–535.Google Scholar
[17] Puri, P. S. (1966) On the homogeneous birth-and-death process and its integral. Biometrika 53, 61–71.CrossRefGoogle ScholarPubMed
[18] Puri, P. S. (1969) Some limit theorems on branching processes and certain related processes. Sankhya, 31, 57–74.Google Scholar
[19] Puri, P. S. (1969) A quantal response process associated with integrals of certain growth processes. To appear in the Proc. Symp. on Mathematical Aspects of Life Sciences, held at Queens University.Google Scholar
[20] Puri, P. S. (1969) Some new results in the mathematical theory of phage-reproduction. J. Appl. Prob. 6, 493–504.CrossRefGoogle Scholar
[21] Puri, P. S. (1970) A method for studying the integral functionals of stochastic processes with applications: II. Sojourn time distributions for Markov chains. Submitted for publication.Google Scholar
[22] Puri, P. S. (1970) A method for studying the integral functionals of stochastic processes with applications: III. Birth and death processes. To appear in Proc. 6th Berkeley Symp. Math. Statist. Prob. Google Scholar
[23] Pyke, R. (1961) Markov renewal processes with finitely many states. Ann. Math. Statist. 32, 1243–1259.Google Scholar
[24] Pyke, R. and Schaufele, R. A. (1964) Limit theorems for Markov renewal processes. Ann. Math. Statist. 35, 1746–1764.Google Scholar
[25] Runnenburg, J. T. (1965) On the use of the method of collective marks in queueing theory. Proc. Symp. on Congestion Theory. U. North Carolina Press.Google Scholar
[26] Smith, W. L. (1955) Regenerative stochastic processes. Proc. Roy. Soc. London, A232, 6–31.Google Scholar
[27] Takács, L. (1958) On a sojourn time problem. Theor. Probability Appl. 3, 58–65.Google Scholar
[28] Takács, L. (1959) On a sojourn time problem in the theory of stochastic processes. Trans. Amer. Math. Soc. 93, 531–540.Google Scholar
[29] Taussky-Todd, O. (1949) A recurring theorem on determinants. Amer. Math. Monthly, 56, 672–676.Google Scholar