Published online by Cambridge University Press: 14 July 2016
1. In 1923 Eggenberger and Pólya introduced the following ‘urn scheme’ as a model for the development of a contagious phenomenon. A box contains b black and r red balls, and a ball is drawn from it at random with ‘double replacement’ (i.e. whatever ball is drawn, it is returned to the box together with a fresh ball of the same colour); the procedure is then continued indefinitely. A slightly more complicated version with m-fold replacement is sometimes discussed, but it will be sufficient for our purposes to keep m = 2 and it will be convenient further to simplify the scheme by taking b = r = 1 as the initial condition. We shall however generalise the scheme in another direction by allowing an arbitrary number k(≧2) of colours. Thus initially the box will contain k differently coloured balls and successive random drawings will be followed by double replacement as before. We write sn (a k-vector with jth component 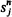 ) for the numerical composition of the box immediately after the nth replacement, so that
) for the numerical composition of the box immediately after the nth replacement, so that 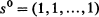 and we observe that
and we observe that 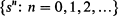 is a Markov process for which the state-space consists of all ordered k-ads of positive integers, the (constant) transition-probability matrix having elements determined by
is a Markov process for which the state-space consists of all ordered k-ads of positive integers, the (constant) transition-probability matrix having elements determined by
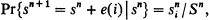 where Sn is the sum of the components of sn and (e(i))j = δij. We shall calculate the Martin boundary for this Markov process, and point out some applications to stochastic models for population growth.
where Sn is the sum of the components of sn and (e(i))j = δij. We shall calculate the Martin boundary for this Markov process, and point out some applications to stochastic models for population growth.