Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-09T03:57:22.430Z Has data issue: false hasContentIssue false
  • English
  • Français

Markov chains in small time intervals

Published online by Cambridge University Press:  14 July 2016

Stig I. Rosenlund
Stig I. Rosenlund*
Affiliation:
University of Göteborg
*
∗Postal address: Västmannagatan 93, S-113 43 Stockholm, Sweden.
Get access Rights & Permissions [Opens in a new window]

Abstract

For a time-homogeneous continuous-parameter Markov chain we show that as t → 0 the transition probability pn,j (t) is at least of order 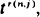where r(n, j) is the minimum number of jumps needed for the chain to pass from n to j. If the intensities of passage are bounded over the set of states which can be reached from n via fewer than r(n, j) jumps, this is the exact order.

Keywords

BIRTH-DEATH PROCESSLOCAL BEHAVIOURMARKOV CHAIN
Type
Short Communications
Information
Journal of Applied Probability , Volume 18 , Issue 3 , September 1981 , pp. 747 - 751
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. 2, 2nd edn. Wiley, New York.Google Scholar
Rosenlund, S. I. (1978a) Transition probabilities for a truncated birth-death process. Scand. J. Statist. 5, 119–122.Google Scholar
Rosenlund, S. I. (1978b) Controlling a Markovian queue at equidistant time epochs. Trans. 8th Prague Conf. Information Theory, Statistical Decision Functions, Random Processes, Vol. B, ed. Driml, M. Academia, Prague, 129–143.Google Scholar