Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T17:09:08.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Limiting results for arrays of binary random variables on rectangular lattices under sparseness conditions

Published online by Cambridge University Press:  14 July 2016

Roy Saunders ,
Richard J. Kryscio  and
Gerald M. Funk
Roy Saunders*
Affiliation:
Northern Illinois University
Richard J. Kryscio*
Affiliation:
Northern Illinois University
Gerald M. Funk*
Affiliation:
Northern Illinois University
*
∗ Postal address: Department of Mathematical Sciences, Northern Illinois University, DeKalb, Illinois 60115, U.S.A.
∗ Postal address: Department of Mathematical Sciences, Northern Illinois University, DeKalb, Illinois 60115, U.S.A.
∗ Postal address: Department of Mathematical Sciences, Northern Illinois University, DeKalb, Illinois 60115, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

In this article we give limiting results for arrays {Xij (m, n) (i, j) 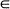Dmn} of binary random variables distributed as particular types of Markov random fields over m x n rectangular lattices Dmn. Under some sparseness conditions which restrict the number of Xij (m, n)'s which are equal to one we show that the random variables (l = 1, ···, r) converge to independent Poisson random variables for 0 < d1 < d2 < · ·· < dr when m→∞ nd∞. 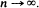The particular types of Markov random fields considered here provide clustering (or repulsion) alternatives to randomness and involve several parameters. The limiting results are used to consider statistical inference for these parameters. Finally, a simulation study is presented which examines the adequacy of the Poisson approximation and the inference techniques when the lattice dimensions are only moderately large.

Keywords

MARKOV RANDOM FIELDLIMITING DISTRIBUTIONBINARY VARIABLESSPARSENESSCLUSTERINGLATTICEPOISSONNEAREST NEIGHBOR
Type
Research Papers
Information
Journal of Applied Probability , Volume 16 , Issue 3 , September 1979 , pp. 554 - 566
Copyright
Copyright © Applied Probability Trust 1979 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research partially supported by the National Science Foundation Grant No. MCS 77–03582.

References

Besag, J. E. (1974) Spatial interaction and the statistical analysis of lattice systems. J. R. Statist. Soc.B 36, 192–235.Google Scholar
Bloemena, A. R. (1964) Sampling from a Graph. Mathematical Centre Tracts 2, Amsterdam.Google Scholar
Curtiss, J. H. (1942) A note on the theory of moment generating functions. Ann. Math. Statist. 13, 430–433.Google Scholar
David, F. N. and Barton, D. E. (1962) Combinatorial Chance. Griffin, London.Google Scholar
Feller, W. (1966) An Introduction to Probability Theory and its Applications, Volume II. Wiley, New York.Google Scholar
Hafner, R. (1972) The asymptotic distribution of random clumps. Computing 10, 335–351.Google Scholar
Hafner, R. (1973) Convergence of point complexes in Zn to Poisson process. Theory Prob. Appl. 18, 131–149.Google Scholar
Kozakiewicz, W. (1947) On the convergence of sequences of moment generating functions. Ann. Math. Statist. 18, 61–69.Google Scholar
Loève, M. (1963) Probability Theory. Van Nostrand, Princeton, N. J.Google Scholar
Ripley, B. D. (1976) The second-order analysis of stationary point processes. J. Appl. Prob. 13, 255–266.Google Scholar
Saunders, R. and Funk, G. M. (1977) Poisson limits for a clustering model of Strauss. J. Appl. Prob. 14, 776–784.Google Scholar
Strauss, D. J. (1975a) Analyzing binary lattice data with the nearest-neighbor property. J. Appl. Prob. 12, 702–712.Google Scholar
Strauss, D. J. (1975b) A model for clustering. Biometrika 62, 467–475.Google Scholar
Strauss, D. J. (1977) Clustering on coloured lattices. J. Appl. Prob. 14, 135–143.Google Scholar