Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T05:10:07.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for out guesses with mean-guided second guessing

Published online by Cambridge University Press:  14 July 2016

Jiunn Tzon Hwang  and
James V. Zidek
Jiunn Tzon Hwang*
Affiliation:
Cornell University
James V. Zidek*
Affiliation:
University of British Columbia
*
∗ Postal address: Department of Mathematics, Cornell University, White Hall, Ithaca, NY 14850, U.S.A.
∗∗ Postal address: Department of Mathematics, The University of British Columbia, #121-1984 Mathematics Rd, Vancouver, B.C., Canada V6T 1Y4.
Get access Rights & Permissions [Opens in a new window]

Abstract

A second guesser, G2, proposes to guess ‘smaller' or ‘larger' on each of n contests, i, according as 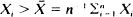, or 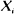where Xi, i = 1, ···, n are the revealed guesses of the first guesser, G1. G2 wins contest i if his assertion about the size of the target quantity θi, is more accurate than that of G1, Xi, i = 1, ···, n. Otherwise G 1 is the winner. Laws of large numbers are derived for G2's win totals for arbitrary configurations of θi. Limiting distributions are obtained for the first guesser's win totals in two special cases, the first where the θi are highly concentrated and the second where they are widely dispersed. G2 enjoys an enormous advantage over G1 in the former case, as intuition would suggest.

Keywords

SECOND GUESSINGREGRESSION TOWARD THE MEAN
Type
Research Papers
Information
Journal of Applied Probability , Volume 19 , Issue 2 , June 1982 , pp. 321 - 331
Copyright
Copyright © Applied Probability Trust 1982 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This research was supported by the National Science Foundation of the United States under grants NSF MCS-80-03568 and NSF MCS-782-4175.

References

Chow, Y. S. and Teicher, H. (1979) Probability Theory, Independence, Interchangeability, Martingales. Springer-Verlag, New York.Google Scholar
Chung, K. L. (1968) A Course in Probability Theory. Harcourt, Brace and World, New York.Google Scholar
Pittenger, A. (1980) Success probabilities for second guessers. J. Appl. Prob. 17, 1133–1137.CrossRefGoogle Scholar
Steele, J. M. and Zidek, J. V. (1980) Optimal strategies for second guessers. J. Amer. Statist. Assoc. 75, 596–601.CrossRefGoogle Scholar