Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Balan, Raluca M.
and
Louhichi, Sana
2009.
Convergence of Point Processes with Weakly Dependent Points.
Journal of Theoretical Probability,
Vol. 22,
Issue. 4,
p.
955.
Zhang, Chenhua
and
McCormick, William P.
2012.
Asymptotic properties of the tail distribution and Hill’s estimator for shot noise sequence.
Extremes,
Vol. 15,
Issue. 4,
p.
407.
Balan, Raluca
2014.
Regular Variation of Infinite Series of Processes with Random Coefficients.
Stochastic Models,
Vol. 30,
Issue. 3,
p.
420.
Roozegar, Rasool
2017.
Limiting behavior of randomly weighted averages of symmetric heavy-tailed random variables.
Communications in Statistics - Theory and Methods,
Vol. 46,
Issue. 9,
p.
4539.
Krizmanić, Danijel
2019.
Functional convergence for moving averages with heavy tails and random coefficients.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 16,
Issue. 1,
p.
729.
Hosseini, Seyed Mohammad
and
Nezakati, Ahmad
2019.
Complete Moment Convergence for the Dependent Linear Processes with Random Coefficients.
Acta Mathematica Sinica, English Series,
Vol. 35,
Issue. 8,
p.
1321.
Owada, Takashi
2019.
Topological crackle of heavy-tailed moving average processes.
Stochastic Processes and their Applications,
Vol. 129,
Issue. 12,
p.
4965.
Hosseini, S. Mohammad
and
Nezakati, Ahmad
2020.
Convergence rates in the law of large numbers for END linear processes with random coefficients.
Communications in Statistics - Theory and Methods,
Vol. 49,
Issue. 1,
p.
88.
Krizmanić, Danijel
2022.
A functional limit theorem for moving averages with weakly dependent heavy-tailed innovations.
Brazilian Journal of Probability and Statistics,
Vol. 36,
Issue. 1,
Krizmanić, Danijel
2022.
Maxima of linear processes with heavy‐tailed innovations and random coefficients.
Journal of Time Series Analysis,
Vol. 43,
Issue. 2,
p.
238.
Krizmanić, Danijel
2023.
A functional limit theorem for self-normalized linear processes with random coefficients and i.i.d. heavy-tailed innovations.
Lithuanian Mathematical Journal,
Vol. 63,
Issue. 3,
p.
305.
Meng, Bing
Wang, Dingcheng
and
Wu, Qunying
2023.
Convergence of asymptotically almost negatively associated random variables with random coefficients.
Communications in Statistics - Theory and Methods,
Vol. 52,
Issue. 9,
p.
2931.
Krizmanić, Danijel
2023.
Joint functional convergence of partial sums and maxima for moving averages with weakly dependent heavy-tailed innovations and random coefficients
.
Latin American Journal of Probability and Mathematical Statistics,
Vol. 20,
Issue. 2,
p.
1247.
Meng, Bing
and
Wu, Qunying
2024.
Convergence of asymptotically negatively associated random variables with random coefficients.
Communications in Statistics - Theory and Methods,
Vol. 53,
Issue. 8,
p.
2961.


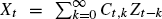 , generated by an array, {
, generated by an array, {