Hostname: page-component-6bf8c574d5-mggfc Total loading time: 0 Render date: 2025-02-23T22:32:21.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Last exit time until first exit time for spectrally negative Lévy processes

Part of: Mathematical economics Stochastic processes Inference from stochastic processes

Published online by Cambridge University Press:  24 January 2025

Xiaofeng Yang ,
José M. Pedraza Open the ORCID record for José M. Pedraza [Opens in a new window]  and
Bin Li
Xiaofeng Yang*
Affiliation:
Central South University
José M. Pedraza*
Affiliation:
The University of Manchester
Bin Li*
Affiliation:
University of Waterloo
*
*Postal address: School of Mathematics and Statistics, Central South University, Changsha, Hunan, 410083, China. Email: [email protected]
**Postal address: Department of Mathematics, The University of Manchester, Manchester, M13 9PL, UK. Email: [email protected]
***Postal address: Department of Statistics and Actuarial Science, University of Waterloo, Waterloo, ON, N2L 3G1, Canada. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the last exit time that a spectrally negative Lévy process is below zero until it reaches a positive level b, denoted by 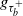$g_{\tau_b^+}$. We generalize the results of the infinite-horizon last exit time explored by Chiu and Yin (2005) by incorporating a random horizon 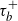$\tau_b^+$, which represents the first passage time above b. We derive an explicit expression for the joint Laplace transform of 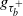$g_{\tau_b^+}$ and 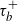$\tau_b^+$ by utilizing a hybrid observation scheme approach proposed by Li, Willmot, and Wong (2018). We further study the optimal prediction of 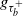$g_{\tau_b^+}$ in the 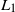$L_1$ sense, and find that the optimal stopping time is the first passage time above a level 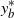$y_b^{\ast}$, with an explicit characterization of the stopping boundary 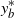$y_b^{\ast}$. As examples, Brownian motion with drift and the Cramér–Lundberg model with exponential jumps are considered.

Keywords

Last exit timefirst exit timespectrally negative Lévy processesdistributionoptimal predictionoptimal stopping

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes 60G40: Stopping times; optimal stopping problems; gambling theory
Secondary: 91B30: Risk theory, insurance 62M20: Prediction
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albrecher, H., Ivanovs, J. and Zhou, X. (2016). Exit identities for Lévy processes observed at Poisson arrival times. Bernoulli 22, 1364–1382.CrossRefGoogle Scholar
Baurdoux, E. J. (2009). Last exit before an exponential time for spectrally negative Lévy processes. J. Appl. Prob. 46, 542–558.CrossRefGoogle Scholar
Baurdoux, E. J. and Pedraza, J. M. (2020). Predicting the last zero of a spectrally negative Lévy process. In XIII Symposium on Probability and Stochastic Processes. Birkhäuser, Cham, pp. 77–105.CrossRefGoogle Scholar
Baurdoux, E. J. and Pedraza, J. M. (2023). Predicting the last zero before an exponential time of a spectrally negative Lévy process. Adv. Appl. Prob. 55, 611–642.CrossRefGoogle Scholar
Baurdoux, E. J. and Pedraza, J. M. (2024). $L_p$ optimal prediction of the last zero of a spectrally negative Lévy process. Ann. Appl. Prob. 34, 1350–1402.CrossRefGoogle Scholar
Bertoin, J. (1998). Lévy Processes. Cambridge University Press.Google Scholar
Bichteler, K. (2002). Stochastic Integration with Jumps. Cambridge University Press.CrossRefGoogle Scholar
Cai, C. and Li, B. (2018). Occupation times of intervals until last passage times for spectrally negative Lévy processes. J. Theoret. Prob. 31, 2194–2215.CrossRefGoogle Scholar
Carr, P. (1998). Randomization and the American put. Rev. Financial Studies 11, 597–626.CrossRefGoogle Scholar
Chiu, S. N. and Yin, C. (2005). Passage times for a spectrally negative Lévy process with applications to risk theory. Bernoulli 11, 511–522.Google Scholar
Chung, K. L. (1976). Excursions in Brownian motion. Ark. Mat. 14, 155–177.CrossRefGoogle Scholar
Du Toit, J., Peskir, G. and Shiryaev, A. (2008). Predicting the last zero of Brownian motion with drift. Stochastics 80, 229–245.CrossRefGoogle Scholar
Egami, M. and Kevkhishvili, R. (2020). Time reversal and last passage time of diffusions with applications to credit risk management. Finance Stoch. 24, 795–825.CrossRefGoogle Scholar
Getoor, R. and Sharpe, M. (1973). Last exit times and additive functionals. Ann. Prob. 1, 550–569.CrossRefGoogle Scholar
Glover, K. and Hulley, H. (2014). Optimal prediction of the last-passage time of a transient diffusion. SIAM J. Control Optim. 52, 3833–3853.CrossRefGoogle Scholar
Kuznetsov, A., Kyprianou, A. E. and Rivero, V. (2013). The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II, Springer, Berlin, pp. 97–186.Google Scholar
Kyprianou, A. E. (2014). Fluctuations of Lévy Processes with Applications. Springer, Berlin.CrossRefGoogle Scholar
Landriault, D., Li, B., Wong, J. T. and Xu, D. (2018). Poissonian potential measures for Lévy risk models. Insurance Math. Econom. 82, 152–166.CrossRefGoogle Scholar
Li, B., Willmot, G. E. and Wong, J. T. (2018). A temporal approach to the Parisian risk model. J. Appl. Prob. 55, 302–317.CrossRefGoogle Scholar
Li, Y., Yin, C. and Zhou, X. (2017). On the last exit times for spectrally negative Lévy processes. J. Appl. Prob. 54, 474–489.CrossRefGoogle Scholar
Peskir, G. and Shiryaev, A. (2006). Optimal Stopping and Free-Boundary Problems. Birkhäuser, Basel.Google Scholar
Salminen, P. (1984). One-dimensional diffusions and their exit spaces. Math. Scand. 54, 209–220.CrossRefGoogle Scholar
Sato, K.-I. (1999). Lévy Processes and Infinitely Divisible Distributions. Cambridge University Press.Google Scholar