Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T18:33:24.779Z Has data issue: false hasContentIssue false
  • English
  • Français

Large deviations of tail estimators based on the Pareto approximation

Published online by Cambridge University Press:  14 July 2016

Richard L. Smith  and
Ishay Weissman
Richard L. Smith*
Affiliation:
University of Surrey
Ishay Weissman*
Affiliation:
Technion — Israel Institute of Technology
*
∗Postal address: Department of Mathematics, University of Surrey, Guildford GU2 5XH, UK.
∗∗Postal address: Faculty of Industrial Engineering and Management, Technion, Haifa, Israel.
Get access Rights & Permissions [Opens in a new window]

Abstract

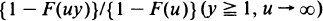We consider the relative error of a tail function when this is approximated by y–α using an estimator of Hill's for α. The results combine recent work of Davis and Resnick on tail estimation with Anderson's work on large deviations in extreme-value theory. Treating separately the domains of attraction of Φα and Λ, we obtain general conditions for the relative error to tend to 0 as u →∞, y → ∞ simultaneously. The results serve as warning against the automatic extrapolation of estimates based on extreme-value approximations.

Keywords

EXTREME VALUE THEORYREGULARLY VARYING FUNCTIONS
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 3 , September 1987 , pp. 619 - 630
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, C. W. (1978) Super-slowly varying functions in extreme value theory. J.R. Statist. Soc. B 40, 197–202.Google Scholar
Anderson, C. W. (1984) Large deviations of extremes. In Statistical Extremes and Applications, ed. Tiago de Oliveira, J., Reidel, Dordrecht, 325–340.Google Scholar
Balkema, A. A. and Haan, , De, L. (1972) On R. Von Mises' condition for the domain of attraction of exp(– e–x) . Ann. Math. Statist. 43, 1352–1354.Google Scholar
Bingham, N. H. and Goldie, C. M. (1982) Extensions of regular variation I: Uniformity and quantifiers. Proc. Lond. Math. Soc. 44, 473–496.CrossRefGoogle Scholar
Cohen, J. P. (1982) Convergence rates for the ultimate and penultimate approximations in extreme value theory. Adv. Appl. Prob. 14, 833–854.Google Scholar
Davis, R. A. and Resnick, S. I. (1984) Tail estimates motivated by extreme value theory. Ann. Statist. 12, 1467–1487.Google Scholar
Galambos, J. (1978) The Asymptotic Theory of Extreme Order Statistics. Wiley, New York.Google Scholar
Gnedenko, B. V. (1943) Sur la distribution limite du terme maximum d'une série aléatoire. Ann. Math. 44, 423–453.CrossRefGoogle Scholar
Goldie, C. M. and Smith, R. L. (1987) Slow variation with remainder: theory and applications. Quart. J. Math. Oxford (2) 38, 45–71.Google Scholar
Haan, , De, L. (1970) On Regular Variation and Its Application to the Weak Convergence of Sample Extremes. Mathematical Centre Tracts 32, Amsterdam.Google Scholar
Haan, , De, L. and Hordijk, A. (1972) The rate of growth of sample maxima. Ann. Math. Statist. 43, 1185–1196.Google Scholar
Hall, P. (1982) On some simple estimates of an exponent of regular variation. J.R. Statist. Soc. B 44, 37–42.Google Scholar
Hill, B. M. (1975) A simple general approach to inference about the tail of a distribution. Ann. Statist. 3, 1163–1174.Google Scholar
Pickands, J., Iii, (1975) Statistical inference using extreme order statistics. Ann. Statist. 3, 119–131.Google Scholar
Smith, R. L. (1982) Uniform rates of convergence in extreme value theory. Adv. Appl. Prob. 14, 600–622.Google Scholar
Smith, R. L. (1987) Estimating tails of probability distributions. Ann. Statist. 15(3).Google Scholar
Weissman, I. (1978) Estimation of parameters and large quantiles based on the k largest observations. J. Amer. Statist. Assoc. 73, 812–815.Google Scholar