Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
GOLDMAN, M. BARRY
SOSIN, HOWARD B.
and
GATTO, MARY ANN
1979.
Path Dependent Options: “Buy at the Low, Sell at the High”.
The Journal of Finance,
Vol. 34,
Issue. 5,
p.
1111.
Simons, Gordon
1983.
A discrete analogue and elementary derivation of ‘Lévy's equivalence’ for Brownian motion.
Statistics & Probability Letters,
Vol. 1,
Issue. 4,
p.
203.
Kan, A.H.G. Rinnooy
and
Timmer, G.T.
1984.
Stochastic Methods for Global Optimization.
American Journal of Mathematical and Management Sciences,
Vol. 4,
Issue. 1-2,
p.
7.
Zehavi, Ephraim
1984.
Estimation of Time of Arrival for Rectangular Pulses.
IEEE Transactions on Aerospace and Electronic Systems,
Vol. AES-20,
Issue. 6,
p.
742.
Deshayes, Jean
and
Picard, Dominique
1985.
Detection of Abrupt Changes in Signals and Dynamical Systems.
Vol. 77,
Issue. ,
p.
103.
Picard, Dominique
1985.
Testing and estimating change-points in time series.
Advances in Applied Probability,
Vol. 17,
Issue. 4,
p.
841.
Abrahams, Julia
1986.
Communications and Networks.
p.
6.
Salminen, Paavo
1987.
Stochastic Differential Systems.
Vol. 96,
Issue. ,
p.
213.
1988.
Extreme Value Theory in Engineering.
p.
341.
Seshadri, V.
1988.
Exponential models, brownian motion, and independence.
Canadian Journal of Statistics,
Vol. 16,
Issue. 3,
p.
209.
Rinnooy Kan, A.H.G.
and
Timmer, G.T.
1989.
Optimization.
Vol. 1,
Issue. ,
p.
631.
Knight, Frank B.
1991.
Seminar on Stochastic Processes, 1990.
p.
241.
Dohi, Tadashi
and
Osaki, Shunji
1992.
Optimal trading of stock options under alternative strategy.
Computers & Mathematics with Applications,
Vol. 24,
Issue. 1-2,
p.
127.
Mathew, George
and
McCormick, William P.
1992.
A conditional limit law result on the location of the maximum of Brownian motion.
Statistics & Probability Letters,
Vol. 13,
Issue. 3,
p.
199.
Kosbar, K.L.
and
Polydoros, A.
1992.
A lower-bound for the error-variance of maximum-likelihood delay estimates of discontinuous pulse waveforms.
IEEE Transactions on Information Theory,
Vol. 38,
Issue. 2,
p.
451.
Calvin, James M.
1993.
Consistency of a myopic Bayesian algorithm for one-dimensional global optimization.
Journal of Global Optimization,
Vol. 3,
Issue. 2,
p.
223.
Dohi, Tadashi
and
Osaki, Shunji
1993.
A note on portfolio optimization with path-dependent utility.
Annals of Operations Research,
Vol. 45,
Issue. 1,
p.
77.
Dohi, T.
Tanaka, H.
Kaio, N.
and
Osaki, S.
1995.
Alternative growth versus security in continuous dynamic trading.
European Journal of Operational Research,
Vol. 84,
Issue. 2,
p.
265.
Lépingle, D.
1995.
Euler scheme for reflected stochastic differential equations.
Mathematics and Computers in Simulation,
Vol. 38,
Issue. 1-3,
p.
119.
Bar-Ilan, Avner
and
Ben-David, Nissim
1996.
An algorithm for evaluating the number of controls in trigger—target models.
Journal of Economic Dynamics and Control,
Vol. 20,
Issue. 8,
p.
1367.


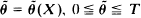 ; (c) the endpoint
; (c) the endpoint 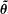 ,
, 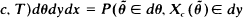 ,
,