Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T04:22:39.555Z Has data issue: false hasContentIssue false
  • English
  • Français

Is the Sibuya distribution a progeny?

Part of: Series expansions Markov processes

Published online by Cambridge University Press:  12 July 2019

Gérard Letac
Gérard Letac*
Affiliation:
Université Paul Sabatier
*
*Postal address: Institut de Mathématiques de Toulouse, Université Paul Sabatier, 118 route de Narbonne 31062 Toulouse, France. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 0 < a < 1, the Sibuya distribution sa is concentrated on the set ℕ+ of positive integers and is defined by the generating function 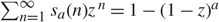$$\sum\nolimits_{n = 1}^\infty s_a (n)z^{{\kern 1pt} n} = 1 - (1 - z)^a$$. A distribution q on ℕ+ is called a progeny if there exists a branching process (Zn)n≥0 such that Z0 = 1, such that 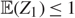$$(Z_1 ) \le 1$$, and such that q is the distribution of 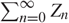$$\sum\nolimits_{n = 0}^\infty Z_n$$. this paper we prove that sa is a progeny if and only if 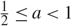$${\textstyle{1 \over 2}} \le a < 1$$. The main point is to find the values of b = 1/a such that the power series expansion of u(1 − (1 − u)b)−1 has nonnegative coefficients.

Keywords

Branching processprogenySibuya law

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 30B10: Power series (including lacunary series)
Type
Research Papers
Information
Journal of Applied Probability , Volume 56 , Issue 1 , March 2019 , pp. 52 - 56
Copyright
© Applied Probability Trust 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B. and Ney, P. E. (1972). Branching Processes. Springer, New York.CrossRefGoogle Scholar
Grey, D. R. (1975). Two necessary conditions for embeddability of a Galton–Watson branching process. Math. Proc. Cambridge Phil. Soc. 78, 339–343.CrossRefGoogle Scholar
Harris, T. H. (1963). The Theory of Branching Processes. Springer, New York.Google Scholar
Kozubowski, T. and Podgórski, K. (2018). A generalized Sibuya distribution. Ann. Inst. Stat. Math. 70, 855–887.CrossRefGoogle Scholar
Sibuya, M. (1979). Generalized hypergeometric, digamma and trigamma distributions. Ann. Inst. Stat. Math. 31, 373–390.CrossRefGoogle Scholar
Toulouse, P. S. (1999). Thèmes de Probabilités et Statistique. Dunod, Paris.Google Scholar
Whittaker, E. T. and Watson, G. N. (1986). A Course in Modern Analysis. Cambridge University Press.Google Scholar