Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-25T03:20:22.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant imbedding and dams with Markovian input rate

Published online by Cambridge University Press:  14 July 2016

P. J. Brockwell  and
N. Pacheco-Santiago
P. J. Brockwell*
Affiliation:
Colorado State University
N. Pacheco-Santiago
Affiliation:
Colorado State University
*
∗Postal address: Department of Statistics, Colorado State University, Fort Collins, CO 80523, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

The method of invariant imbedding, used extensively in astrophysics and in neutron transport theory, is applied to the analysis of dams whose input rate is a finite state-space continuous-parameter Markov chain. Passage-time distributions are considered as functions of the dam capacity. When the release rate is constant the method yields first-order non-linear differential equations with initial conditions obtained from the easily derived behaviour of a dam with zero capacity. Solutions of these equations are given. Some possible correlation functions for the increments of the cumulative input process are examined when the underlying Markov chain is stationary. Finally the analysis is extended to deal with dams having content-dependent release-rate of the form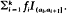

Keywords

CONTINUOUS-TIME STORAGE MODELINTEGRAL OF MARKOV CHAINPASSAGE TIMEINVARIANT IMBEDDINGSTATIONARY DISTRIBUTIONDEPENDENT INPUTS
Type
Research Papers
Information
Journal of Applied Probability , Volume 17 , Issue 3 , September 1980 , pp. 778 - 789
Copyright
Copyright © Applied Probability Trust 1980 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by NSF Grant No. MCS 78–00915.

∗∗

Present address: Quarters #4206C, USAF Academy, CO 80840, U.S.A.

Research presented in partial fulfillment of Ph.D. requirements at Colorado State University and supported by the United States Air Force.

References

[1] Ali Khan, ?. S. and Gani, J. (1968) Infinite dams with inputs forming a Markov chain. J. Appl. Prob. 5, 72–83.Google Scholar
[2] Ambarzumian, V. A. (1943) Diffuse reflection of light by a foggy medium. C . R. Acad. Sci. U.R.S.S. 38, 229.Google Scholar
[3] Anderson, B. D. O. and Kailath, T. (1979) Forwards and backwards models for finite-state Markov processes. Adv. Appl. Prob. 11, 118–133.Google Scholar
[4] Bellman, R. and Kalaba, R. (1961) Transport theory and invariant imbedding. Proc. Symp. Appl. Math. 11, 206.Google Scholar
[5] Brockwell, P. J. (1972) A storage model in which the net growth-rate is a Markov chain. J. Appl. Prob. 9, 129–139.Google Scholar
[6] Brockwell, P. J. (1973) On the spectrum of a class of matrices arising in storage theory. Z. Wahrscheinlichkeitsth. 25, 253–260.Google Scholar
[7] Brockwell, P. J. (1977) Stationary distributions for dams with additive input and content-dependent release rate. Adv. Appl. Prob. 9, 645–663.Google Scholar
[8] Chandrasekhar, S. (1960) Radiative Transfer , 2nd edn. Dover, New York.Google Scholar
[9] Çinlar, E. and Pinsky, M. (1971) A stochastic integral in storage theory. Z. Wahrscheinlichkeitsth. 2, 180–224.Google Scholar
[10] Erickson, R. V. (1972) Stationary measures for a class of storage models driven by a Markov chain. Ann. Math. Statist. 43, 997–1007.Google Scholar
[11] Feller, W. (1971) An Introduction to Probability Theory and its Applications , Vol. 2, 2nd edn. Wiley, New York.Google Scholar
[12] Harrison, J. M. and Resnick, S. I. (1975) The stationary distribution and first exit probabilities of a storage process with general release rate. Math. Operat. Res. 1, 347–358.Google Scholar
[13] Keilson, J. and Subba Rao, S. (1971) A process with chain-dependent growth-rate. Part II. The ruin and ergodic problems. Adv. Appl. Prob. 3, 315–338.Google Scholar
[14] Kendall, D. G. (1957) Some problems in the theory of dams. J. R. Statist. Soc. B 19, 207–212.Google Scholar
[15] Mcneil, D. R. (1972) A simple model for a dam in continuous-time with Markovian input. Z. Wahrscheinlichkeitsth. 21, 241–254.CrossRefGoogle Scholar
[16] Moran, P. A. P. (1959) The Theory of Storage. Methuen, London.Google Scholar
[17] Moran, P. A. P. (1969) A theory of dams with continuous input and a general release rule. J. Appl. Prob. 6, 88–98.Google Scholar
[18] Odoom, S. and Lloyd, E. H. (1965) A note on the equilibrium distribution of levels in a semi-infinite reservoir subject to Markovian inputs and unit withdrawals. J. Appl. Prob. 2, 215–222.CrossRefGoogle Scholar
[19] Pakes, A. G. (1973) On dams with Markóvian inputs. J. Appl. Prob. 10, 317–329.Google Scholar