Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T15:54:27.230Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariance principles in queueing theory

Published online by Cambridge University Press:  14 July 2016

Michael Alex  and
Josef Steinebach
Michael Alex*
Affiliation:
University of Marburg
Josef Steinebach*
Affiliation:
University of Hannover
*
∗ Postal address: Fachbereich Mathematik, Universität Marburg, Hans-Meerwein Strasse, D-3550 Marburg, W. Germany.
∗∗ Postal address: Institute für Math. Stochastik, Universität Hannover, Welfengarten 1, D-3000 Hannover, W. Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

Several stochastic processes in queueing theory are based upon compound renewal processes 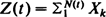. For queues in light traffic, however, the summands {Xk}and the renewal counting process {N(t)} are typically dependent on each other. Making use of recent invariance principles for such situations, we present some weak and strong approximations for the GI/G/1 queues in light and heavy traffic. Some applications are discussed including convergence rate statements or Darling–Erdös-type extreme value theorems for the processes under consideration.

Keywords

STRONG APPROXIMATIONSGI/G/I QUEUEDARLING—ERDÖS TYPE THEOREMSEXTREME VALUE LIMITING DISTRIBUTIONS
Type
Research Papers
Information
Journal of Applied Probability , Volume 26 , Issue 4 , December 1989 , pp. 845 - 857
Copyright
Copyright © Applied Probability Trust 1989 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alex, M. (1988) Invarianzprinzipien in der Warteschlangen- und Risikotheorie. Diplomarbeit, University of Marburg.Google Scholar
Chung, K. L. (1968) A Course in Probability Theory. Harcourt, Brace and World, New York.Google Scholar
Csörgö, M. and Revesz, P. (1981) Strong Approximations in Probability and Statistics. Academic Press, New York.Google Scholar
Csörgö, M., Deheuvels, P. and Horvath, L. (1987) An approximation of stopped sums with applications in queueing theory. Adv. Appl. Prob. 19, 674–690.Google Scholar
Darling, D. A. and Erdós, P. (1956) A limit theorem for the maximum of normalized sums of independent random variables. Duke Math. J. 23, 143–155.Google Scholar
Darling, D. A. and Siegert, A. (1953) The first passage time problem for continuous Markov processes. Ann. Math. Statist. 24, 624–639.Google Scholar
Gieβing, R. and Steinebach, J. (1988) Invariance principles for compound renewal processes with applications. Proc. 4th Prague Symp. on Asymptotic Statistics, 1988. To appear.Google Scholar
Gut, A. (1974) On the moments and limit distributions of some first passage times. Ann. Prob. 2, 277–308.Google Scholar
Gut, A. (1988) Stopped Random Walks. Springer-Verlag, Berlin.Google Scholar
Iglehart, D. L. (1971) Functional limit theorems for the queue GI/G/1 in light traffic. Adv. Appl. Prob. 3, 269–281.CrossRefGoogle Scholar
Iglehart, D. L. (1973) Weak convergence in queueing theory. Adv. Appl. Prob. 5, 570–594.Google Scholar
Iglehart, D. L. and Whitt, W. (1970a) Multiple channel queues in heavy traffic, I. Adv. Appl. Prob. 2, 150–177.Google Scholar
Iglehart, D. L. and Whitt, W. (1970b) Multiple channel queues in heavy traffic, II: sequences, networks and batches. Adv. Appl. Prob. 2, 355–369.Google Scholar
Kennedy, D. P. (1972a) Rates of convergence for queues in heavy traffic, I. Adv. Appl. Prob. 4, 357–381.Google Scholar
Kennedy, D. P. (1972b) Rates of convergence for queues in heavy traffic, II: sequences of queueing systems. Adv. Appl. Prob. 4, 382–391.Google Scholar
Kingman, J. F. C. (1962) On queues in heavy traffic. J. R. Statist. Soc. B 24, 383–392.Google Scholar
Kingman, J. F. C. (1965) The heavy traffic approximation in the theory of queues. Proc. Symp. Congestion Theory, University of North Carolina Press, Chapel Hill, pp. 137–169.Google Scholar
Rosenkrantz, W. (1980) On the accuracy of Kingman's heavy traffic approximation in the theory of queues. Z. Wahrscheinlichkeitsth. 51, 115–121.CrossRefGoogle Scholar
Steinebach, J. (1988) Invariance principles for renewal processes when only moments of low order exist. J. Multiv. Anal. 26, 169–183.Google Scholar
Whitt, W. (1968) Weak Convergence Theorems for Queues in Heavy Traffic. Ph. D. Thesis, Cornell University. Tech. Rep. No. 2, Dept. Oper. Res., Stanford University.Google Scholar
Whitt, W. (1972) Embedded renewal processes in the GI/G/s queue. J. Appl. Prob. 9, 650–658.Google Scholar