Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T17:53:46.105Z Has data issue: false hasContentIssue false
  • English
  • Français

Intersections of random sets

Part of: Global differential geometry Geometric probability and stochastic geometry

Published online by Cambridge University Press:  17 January 2022

Jacob Richey  and
Amites Sarkar
Jacob Richey*
Affiliation:
University of British Columbia
Amites Sarkar*
Affiliation:
Western Washington University
*
*Postal address: 1984 Mathematics Rd, VancouverBC V6T 1Z2, Canada. Email: [email protected]
**Postal address: 516 High Street, BellinghamWA 98225, USA. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a variant of a classical coverage process, the Boolean model in 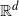$\mathbb{R}^d$ . Previous efforts have focused on convergence of the unoccupied region containing the origin to a well-studied limit C. We study the intersection of sets centered at points of a Poisson point process confined to the unit ball. Using a coupling between the intersection model and the original Boolean model, we show that the scaled intersection converges weakly to the same limit C. Along the way, we present some tools for studying statistics of a class of intersection models.

Keywords

Poisson processrandom tessellationCrofton cell

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 53C65: Integral geometry
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 1 , March 2022 , pp. 131 - 151
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adell, J. A. and Jodrá, P. (2006). Exact Kolmogorov and total variation distances between some familiar discrete distributions. J. Inequal. Appl. 2006, 64307.10.1155/JIA/2006/64307CrossRefGoogle Scholar
Billingsley, P. (1995). Probability and Measure, 3rd edn. John Wiley, New York.Google Scholar
Böröczky, K. (2004). Finite Packing and Covering. Cambridge University Press.CrossRefGoogle Scholar
Calka, P. (2003). An explicit expression for the distribution of the number of sides of the typical Poisson–Voronoi cell. Adv. Appl. Prob. 35, 863–870.CrossRefGoogle Scholar
Calka, P. (2019). Some classical problems in random geometry. In Stochastic Geometry, ed. Coupier, D. (Lect. Notes Math. 2237), Springer, Berlin, pp. 1–43.Google Scholar
Calka, P., Michel, J. and Paroux, K. (2009). Refined convergence for the Boolean model. Adv. Appl. Prob. 41, 940–957.10.1017/S0001867800003670CrossRefGoogle Scholar
Calka, P. and Schreiber, T. (2005). Limit theorems for the typical Poisson–Voronoi cell and the Crofton cell with a large inradius. Ann. Prob. 33, 1625–1642.CrossRefGoogle Scholar
Cannone, C. (2017). A short note on Poisson tail bounds. Available at http://www.cs.columbia.edu/ ccanonne/files/misc/2017-poissonconcentration.pdf.Google Scholar
Erdös, P. and Rényi, A. (1961). On a classical problem of probability theory. Magyar Tudományos Akadémia Matematikai Kutató Intézetének Közleményei 6, 215–220.Google Scholar
Folland, G. B. (1999). Real Analysis. John Wiley, New York.Google Scholar
Franceschetti, M. and Meester, R. (2007). Random Networks for Communication. Cambridge University Press.Google Scholar
Gilbert, E. (1961). Random plane networks. J. Soc. Indust. Appl. Math. 9, 533–543.CrossRefGoogle Scholar
Gilbert, E. (1965). The probability of covering a sphere with N circular caps. Biometrika 56, 323–330.10.1093/biomet/52.3-4.323CrossRefGoogle Scholar
Goudsmit, S. (1945). Random distribution of lines in a plane. Rev. Mod. Phys. 17, 321–322.10.1103/RevModPhys.17.321CrossRefGoogle Scholar
Hall, P. (1985). On the coverage of k-dimensional space by k-dimensional spheres. Ann. Prob. 13, 991–1002.CrossRefGoogle Scholar
Hall, P. (1985). On continuum percolation. Ann. Prob. 13, 1250–1266.10.1214/aop/1176992809CrossRefGoogle Scholar
Hall, P. (1988). Introduction to the Theory of Coverage Processes. John Wiley, New York.Google Scholar
Haenggi, M. (2013). Stochastic Geometry for Wireless Networks. Cambridge University Press.Google Scholar
Janson, S. (1986). Random coverings in several dimensions. Acta Math. 156, 83–118.CrossRefGoogle Scholar
Kingman, J. F. C. (1992). Poisson Processes. Clarendon Press, Oxford.Google Scholar
Matheron, G. (1975). Random Sets and Integral Geometry. John Wiley, New York.Google Scholar
Meester, R. and Roy, R. (1996). Continuum Percolation. Cambridge University Press.CrossRefGoogle Scholar
Michel, J. and Paroux, K. (2003). Local convergence of the Boolean shell model towards the thick Poisson hyperplane process in the Euclidean space. Adv. Appl. Prob. 35, 354–361.10.1017/S0001867800012271CrossRefGoogle Scholar
Miles, R. (1964). Random polygons determined by random lines in a plane I. Proc. Nat. Acad. Sci. USA 52, 901–907.10.1073/pnas.52.4.901CrossRefGoogle Scholar
Miles, R. (1964). Random polygons determined by random lines in a plane II. Proc. Nat. Acad. Sci. USA 52, 1157–1160.CrossRefGoogle Scholar
Molchanov, I. (1996). A limit theorem for scaled vacancies of the Boolean model. Stoch. Stoch. Rep. 58, 45–65.10.1080/17442509608834068CrossRefGoogle Scholar
Robbins, H. E. (1944). On the measure of a random set. Ann. Math. Statist. 15, 70–74.CrossRefGoogle Scholar
Santambrogio, F. (2015). Optimal Transport for Applied Mathematicians. Birkhauser, Basel.10.1007/978-3-319-20828-2CrossRefGoogle Scholar
Santaló, L. (1976). Integral Geometry and Geometric Probability. Addison Wesley, Boston.Google Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.CrossRefGoogle Scholar