If F(s) is the probability generating function of a non-negative random variable, the nth functional iterate Fn(s) = Fn–1 (F(s)) generates the distribution of the size of the nth generation of a simple branching process. In general it is not possible to obtain explicit formulae for many quantities involving Fn(s), and this paper considers certain bounds and approximations. 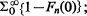Bounds are found for the Koenigs-type iterates limn→∞m−n {1−Fn(s)}, 0 ≦ s ≦ 1 where m = F′(1) < 1 and F′′(1) < ∞; for the expected time to extinction and for the limiting conditional-distribution generating function limn→∞{Fn(s) − Fn(0)} [1 – Fn(0)]–1. Particular attention is paid to the case F(s) = exp {m(s − 1)}.