Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-04T19:38:40.369Z Has data issue: false hasContentIssue false
  • English
  • Français

The identifiability of mixtures of distributions

Published online by Cambridge University Press:  14 July 2016

G. M. Tallis
G. M. Tallis*
Affiliation:
C.S.I.R.O., New South Wales 2042
Get access Rights & Permissions [Opens in a new window]

Extract

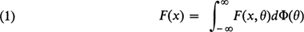This paper considers aspects of the following problem. Let F(x, θ) be a distribution function, d.f., in x for all θ and a Borel measurable function of θ. Define the mixture (Robbins (1948)), where Φ is a d.f., then it is of interest to determine conditions under which F(x) and F(x, θ) uniquely determine Φ. If there is only one Φ satisfying (1), F is said to be an identifiable mixture. Usually a consistency assumption is used whereby it is presumed that there exists at least one solution to (1).

Type
Research Papers
Information
Journal of Applied Probability , Volume 6 , Issue 2 , August 1969 , pp. 389 - 398
Copyright
Copyright © Sheffield: Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Kantorovich, L. V. and Krylov, V. I. (1959) Approximate Methods of Higher Analysis. Translated by Benster, C. D. Noordhoff, Groningen.Google Scholar
Robbins, H. (1948) Mixture of distributions. Ann. Math. Statist. 19, 360–369.Google Scholar
Teicher, H. (1963) Identifiability of finite mixtures. Ann. Math. Statist. 34, 1265–1269.Google Scholar
Tricomi, F. G. (1957) Integral Equations. Interscience Publishers Inc., New York.Google Scholar