Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T17:56:30.644Z Has data issue: false hasContentIssue false
  • English
  • Français

Hitting times of decreasing sets for regenerative processes

Published online by Cambridge University Press:  14 July 2016

K. B. Athreya
K. B. Athreya*
Affiliation:
Iowa State University
*
∗ Postal address: Departments of Mathematics and Statistics, Iowa State University, Ames, IA 50011, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let {X(t): t ≧ 0} be a regenerative process with excursion process {Y(u): 0 ≦ u < T, T} and state space 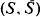. Let An be a sequence of sets in 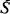such that pn=P(Y(u)∊An for some 0≦ u < T) → 0. Let Vn be the hitting time of An for the process X. This paper gives a variety of conditions on the excursion process Y to obtain limit theorems for Vn. Apart from obtaining an exponential limit in the positive recurrent case, i.e. ET < x, some non-exponential limits are obtained in the null recurrent case. The results are illustrated via the age process.

Keywords

EXCURSION PROCESSPOSITIVE AND NULL RECURRENCEEXPONENTIAL AND NON-EXPONENTIAL LIMITSREGULAR AND SLOW VARIATION
Type
Research Papers
Information
Journal of Applied Probability , Volume 25 , Issue 1 , March 1988 , pp. 89 - 96
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported in part by a grant from the National Science Foundation, DMS 85 02311.

References

[1] Athreya, K. B. and Ney, P. (1978) A new approach to the limit theory of Markov chains. Trans . Amer. Math. Soc. 245, 493–501.CrossRefGoogle Scholar
[2] Cinlar, E. (1975) Introduction to Stochastic Processes. Prentice Hall, Englewood Cliffs, NJ.Google Scholar
[3] Cogburn, R. (1985) On the distribution of first passage and return times for small sets. Ann. Prob. 13, 1219–1223.Google Scholar
[4] Feller, W. (1971) An Introduction to Probability Theory and its Applications , Vol. 2. Wiley, New York.Google Scholar
[5] Korolyuk, D. V. and Silvestrov, D. S. (1983) Entry times into asymptotically receding domains for ergodic Markov chains. Theory Prob. Appl. 28, 432–441.Google Scholar
[6] Korolyuk, D. V. and Silvestrov, D. S. (1984) Entry times into asymptotically receding regions for processes with semi Markov switchings. Theory Prob. Appl. 29, 558–562.Google Scholar
[7] Lindvall, T. (1976) An invariance principle for thinned random measures. Studia Sci. Math. Hungar. 11, 269–275.Google Scholar
[8] Nummelin, E. (1984) General Irreducible Markov Chains and Nonnegative Operators. Cambridge Tracts in Mathematics 83, Cambridge University Press.Google Scholar
[9] Rootzen, H. (1988) Maxima and exceedances of stationary Markov chains. Adv. Appl. Prob. 20 (2).CrossRefGoogle Scholar