Article contents
Generalized limit theorems for U-max statistics
Published online by Cambridge University Press: 11 July 2022
Abstract
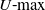 $U{\hbox{-}}\textrm{max}$
statistics were introduced by Lao and Mayer in 2008. Such statistics are natural in stochastic geometry. Examples are the maximal perimeters and areas of polygons and polyhedra formed by random points on a circle, ellipse, etc. The main method to study limit theorems for
$U{\hbox{-}}\textrm{max}$
statistics were introduced by Lao and Mayer in 2008. Such statistics are natural in stochastic geometry. Examples are the maximal perimeters and areas of polygons and polyhedra formed by random points on a circle, ellipse, etc. The main method to study limit theorems for 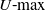 $U{\hbox{-}}\textrm{max}$
statistics is via a Poisson approximation. In this paper we consider a general class of kernels defined on a circle, and we prove a universal limit theorem with the Weibull distribution as a limit. Its parameters depend on the degree of the kernel, the structure of its points of maximum, and the Hessians of the kernel at these points. Almost all limit theorems known so far may be obtained as simple special cases of our general theorem. We also consider several new examples. Moreover, we consider not only the uniform distribution of points but also almost arbitrary distribution on a circle satisfying mild additional conditions.
$U{\hbox{-}}\textrm{max}$
statistics is via a Poisson approximation. In this paper we consider a general class of kernels defined on a circle, and we prove a universal limit theorem with the Weibull distribution as a limit. Its parameters depend on the degree of the kernel, the structure of its points of maximum, and the Hessians of the kernel at these points. Almost all limit theorems known so far may be obtained as simple special cases of our general theorem. We also consider several new examples. Moreover, we consider not only the uniform distribution of points but also almost arbitrary distribution on a circle satisfying mild additional conditions.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by



