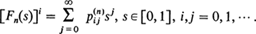Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Papangelou, F.
1968.
A lemma on the Galton-Watson process and some of its consequences.
Proceedings of the American Mathematical Society,
Vol. 19,
Issue. 6,
p.
1469.
Seneta, E.
1968.
The Stationary Distribution of a Branching Process Allowing Immigration: A Remark on the Critical Case.
Journal of the Royal Statistical Society Series B: Statistical Methodology,
Vol. 30,
Issue. 1,
p.
176.
Seneta, E.
1969.
Functional equations and the Galton-Watson process.
Advances in Applied Probability,
Vol. 1,
Issue. 1,
p.
1.
Seneta, E.
1969.
Functional equations and the Galton-Watson process.
Advances in Applied Probability,
Vol. 1,
Issue. 1,
p.
1.
Foster, James H.
and
Williamson, John A.
1971.
Limit theorems for the Galton-Watson process with time-dependent immigration.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 20,
Issue. 3,
p.
227.
Pakes, A. G.
1971.
A branching process with a state dependent immigration component.
Advances in Applied Probability,
Vol. 3,
Issue. 2,
p.
301.
Seneta, E.
1971.
On invariant measures for simple branching processes.
Journal of Applied Probability,
Vol. 8,
Issue. 01,
p.
43.
Yang, Y. S.
1972.
On branching processes allowing immigration.
Journal of Applied Probability,
Vol. 9,
Issue. 1,
p.
24.
Iosifescu, M.
and
Tăutu, P.
1973.
Stochastic processes and applications in biology and medicine I.
Vol. 3,
Issue. ,
p.
11.
Pakes, A. G.
and
Kaplan, Norman
1974.
On the subcritical Bellman-Harris process with immigration.
Journal of Applied Probability,
Vol. 11,
Issue. 4,
p.
652.
Pakes, A. G.
and
Kaplan, Norman
1974.
On the subcritical Bellman-Harris process with immigration.
Journal of Applied Probability,
Vol. 11,
Issue. 04,
p.
652.
Wang, Robert C.
1976.
The extinction time of Markov branching processes.
Journal of Applied Probability,
Vol. 13,
Issue. 2,
p.
345.
Hoppe, Fred M.
1977.
The critical Bienaymé-Galton-Watson process.
Stochastic Processes and their Applications,
Vol. 5,
Issue. 1,
p.
57.
Pakes, Anthony G.
1978.
On the age distribution of a Markov chain.
Journal of Applied Probability,
Vol. 15,
Issue. 1,
p.
65.
Pommerenke, Ch.
1981.
On the stationary measures of critical branching processes.
Zeitschrift f�r Wahrscheinlichkeitstheorie und Verwandte Gebiete,
Vol. 55,
Issue. 3,
p.
305.
Bhattacharjee, Manish C.
1982.
The Class of Mean Residual Lives and Some Consequences.
SIAM Journal on Algebraic Discrete Methods,
Vol. 3,
Issue. 1,
p.
56.
Narayan, Prakash
1982.
On the Extinction Time of a Continuous time Markov Branching Process.
Australian Journal of Statistics,
Vol. 24,
Issue. 2,
p.
160.
Bhattacharjee, M. C.
1987.
The Time to Extinction of Branching Processes and Log-Convexity: I.
Probability in the Engineering and Informational Sciences,
Vol. 1,
Issue. 3,
p.
265.
Vatutin, V. A.
and
Zubkov, A. M.
1987.
Branching processes. I.
Journal of Soviet Mathematics,
Vol. 39,
Issue. 1,
p.
2431.
Griffiths, R. C.
and
Pakes, Anthony G.
1988.
An infinite-alleles version of the simple branching process.
Advances in Applied Probability,
Vol. 20,
Issue. 3,
p.
489.


 and assume, as usual, that 0 <
and assume, as usual, that 0 <