Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-22T14:55:54.267Z Has data issue: false hasContentIssue false
  • English
  • Français

The Galton-Watson process conditioned on the total progeny

Published online by Cambridge University Press:  14 July 2016

Douglas P. Kennedy
Douglas P. Kennedy*
Affiliation:
University of Sheffieldcor1corresp
*
Get access Rights & Permissions [Opens in a new window]

Abstract

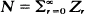Let Zk denote the number in the kth generation of a Galton-Watson process initiated by one individual and let N be the total progeny, i.e., As n → ∞ the limiting behaviour of the process {Zk, 0 ≦ k ≦ n} conditioned on the event {N =n} is studied. The results obtained are of exactly the same form for the subcritical, critical and supercritical cases. This is in marked contrast to the analogous situation got by conditioning on non-extinction by the nth generation and letting n → ∞. In the latter case the limiting results differ in form for the critical and non-critical cases.

Keywords

BRANCHING PROCESSESGALTON-WATSON PROCESSTOTAL PROGENYLIMIT THEOREMSCONDITIONED LIMIT THEOREMS
Type
Short Communications
Information
Journal of Applied Probability , Volume 12 , Issue 4 , December 1975 , pp. 800 - 806
Copyright
Copyright © Applied Probability Trust 1975 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Athreya, K. and Ney, P. (1972) Branching Processes. Springer-Verlag, New York.CrossRefGoogle Scholar
[2] Billingsley, P. (1968) Convergence of Probability Measures. Wiley, New York.Google Scholar
[3] Dwass, M. (1969) The total progeny in a branching process. J. Appl. Prob. 6, 682–686.CrossRefGoogle Scholar
[4] Feller, W. (1966) An Introduction to Probability Theory and its Applications, Volume II. Wiley, New York.Google Scholar
[5] Ibragimov, I. and Linnik, Yu. (1971) Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff, The Netherlands.Google Scholar
[6] Lamperti, J. and Ney, P. (1968) Conditioned branching processes and their limiting diffusions. Theor. Prob. Appl. 13, 126–137.CrossRefGoogle Scholar
[7] Pakes, A. G. (1971) Some limit theorems for the total progeny of a branching process. Adv. Appl. Prob. 3, 176–192.Google Scholar