Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T06:03:38.939Z Has data issue: false hasContentIssue false
  • English
  • Français

Families of birth-death processes with similar time-dependent behaviour

Part of: Markov processes

Published online by Cambridge University Press:  14 July 2016

R. B. Lenin ,
P. R. Parthasarathy ,
W. R. W. Scheinhardt  and
E. A. van Doorn
R. B. Lenin*
Affiliation:
University of Antwerp
P. R. Parthasarathy*
Affiliation:
Indian Institute of Technology
W. R. W. Scheinhardt*
Affiliation:
Eindhoven University of Technology
E. A. van Doorn*
Affiliation:
University of Twente
*
∗Postal address: Department of Mathematics and Computer Science, University of Antwerp, Universiteitsplein 1, B-2610 Wilrijk, Belgium
∗∗Postal address: Department of Mathematics, Indian Institute of Technology, Madras, Chennai 600 036, India
∗∗∗Postal address: Department of Mathematics and Computing Science, Eindhoven University of Technology, P.O. Box 513, 5600 MB Eindhoven, The Netherlands
∗∗∗∗Postal address: Faculty of Mathematical Sciences, University of Twente, P.O. Box 217, 7500 AE Enschede, The Netherlands. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

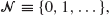We consider birth-death processes taking values in but allow the death rate in state 0 to be positive, so that escape from 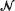is possible. Two such processes with transition functions 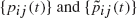are said to be similar if, for all 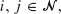there are constants cij such that 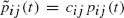for all t ≥ 0. We determine conditions on the birth and death rates of a birth-death process for the process to be a member of a family of similar processes, and we identify the members of such a family. These issues are also resolved in the more general setting in which the two processes are called similar if there are constants cij and ν such that 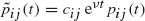for all t ≥ 0.

Keywords

Absorption probabilitychain sequenceinvariant vectortransient behaviourtransition function

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Type
Research Papers
Information
Journal of Applied Probability , Volume 37 , Issue 3 , September 2000 , pp. 835 - 849
Copyright
Copyright © Applied Probability Trust 2000 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M., and Stegun, I. A. (eds.) (1972). Handbook of Mathematical Functions. Dover, New York.Google Scholar
Anderson, W. J. (1991). Continuous-Time Markov Chains. Springer, New York.CrossRefGoogle Scholar
Chihara, T. S. (1978). An Introduction to Orthogonal Polynomials. Gordon and Breach, New York.Google Scholar
Chihara, T. S. (1982). Indeterminate symmetric moment problems. J. Math. Anal. Appl. 85, 331–346.CrossRefGoogle Scholar
Chihara, T. S. (1990). The parameters of a chain sequence. Proc. Amer. Math. Soc. 108, 775–780.CrossRefGoogle Scholar
Di Crescenzo, A. (1994). On certain transformation properties of birth-and-death processes. In Cybernetics and Systems '94, ed. Trappl, R. World Scientific, Singapore, pp. 839–846.Google Scholar
Di Crescenzo, A. (1994). On some transformations of bilateral birth-and-death processes with applications to first passage time evaluations. In SITA '94–-Proc. 17th Symp. Inf. Theory Appl. Hiroshima, Japan, pp. 739–742.Google Scholar
Karlin, S., and McGregor, J. L. (1957). The differential equations of birth-and-death processes, and the Stieltjes moment problem. Trans. Amer. Math. Soc. 85, 489–546.CrossRefGoogle Scholar
Karlin, S., and McGregor, J. L. (1957). The classification of birth and death processes. Trans. Amer. Math. Soc. 86, 366–400.CrossRefGoogle Scholar
Karlin, S. and McGregor, J. L. (1958). Linear growth, birth and death processes. J. Math. Mech. 7, 643–662.Google Scholar
Küchler, U. (1982). Exponential families of Markov processes–-Part II: birth and death processes. Math. Operationsforsch. Statist., Ser. Statist. 13, 219–230.Google Scholar
Ledermann, W., and Reuter, G. E. H. (1954). Spectral theory for the differential equations of simple birth and death processes. Philos. Trans. R. Soc. London, A 246, 321–369.Google Scholar
Letessier, J., and Valent, G. (1986). Dual birth and death processes and orthogonal polynomials. SIAM J. Appl. Math. 46, 393–405.CrossRefGoogle Scholar
Letessier, J., and Valent, G. (1988). Some integral relations involving hypergeometric functions. SIAM J. Appl. Math. 48, 214–221.CrossRefGoogle Scholar
Pollett, P. K. (1988). Reversibility, invariance and μ-invariance. Adv. Appl. Prob. 20, 600–621.CrossRefGoogle Scholar
van Doorn, E. A. (1985). Conditions for exponential ergodicity and bounds for the decay parameter of a birth–death process. Adv. Appl. Prob. 17, 514–530.CrossRefGoogle Scholar
Walker, D. M. (1998). The expected time until absorption when absorption is not certain. J. Appl. Prob. 35, 812–823.CrossRefGoogle Scholar
Waugh, W. A. O'N. (1958). Conditioned Markov processes. Biometrika 45, 241–249.CrossRefGoogle Scholar
Zeifman, A. I. (1998). Some estimates of the rate of convergence for birth and death processes. J. Appl. Prob. 28, 268–277.CrossRefGoogle Scholar