Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Лебедев, Алексей Викторович
and
Lebedev, Alexey Viktorovich
2002.
Экстремумы субэкспоненциального дробового шума.
Математические заметки,
Vol. 71,
Issue. 2,
p.
227.
Lebedev, A. V.
2003.
Extremes of Shot-Noise Fields in the Presence of Regularly Varying Tails.
Theory of Probability & Its Applications,
Vol. 47,
Issue. 4,
p.
702.
Lund, Robert
McCormick, William P.
and
Xiao, Yuanhui
2004.
Limiting properties of Poisson shot noise processes.
Journal of Applied Probability,
Vol. 41,
Issue. 3,
p.
911.
Fasen, Vicky
2005.
Extremes of regularly varying Lévy-driven mixed moving average processes.
Advances in Applied Probability,
Vol. 37,
Issue. 4,
p.
993.
Tang, Qihe
2006.
On convolution equivalence with applications.
Bernoulli,
Vol. 12,
Issue. 3,
Xiao, Yuanhui
and
Lund, Robert
2006.
Inference for Shot Noise.
Statistical Inference for Stochastic Processes,
Vol. 9,
Issue. 1,
p.
77.
Matsui, Muneya
and
Mikosch, Thomas
2010.
Prediction in a Poisson cluster model.
Journal of Applied Probability,
Vol. 47,
Issue. 02,
p.
350.
Weng, Chengguo
Zhang, Yi
and
Tan, Ken Seng
2013.
Tail Behavior of Poisson Shot Noise Processes under Heavy-tailed Shocks and Actuarial Applications.
Methodology and Computing in Applied Probability,
Vol. 15,
Issue. 3,
p.
655.
Budhiraja, Amarjit
and
Nyquist, Pierre
2015.
Large deviations for multidimensional state-dependent shot-noise processes.
Journal of Applied Probability,
Vol. 52,
Issue. 4,
p.
1097.
Alsmeyer, Gerold
Iksanov, Alexander
and
Meiners, Matthias
2015.
Power and Exponential Moments of the Number of Visits and Related Quantities for Perturbed Random Walks.
Journal of Theoretical Probability,
Vol. 28,
Issue. 1,
p.
1.
Budhiraja, Amarjit
and
Nyquist, Pierre
2015.
Large deviations for multidimensional state-dependent shot-noise processes.
Journal of Applied Probability,
Vol. 52,
Issue. 4,
p.
1097.
Matsui, Muneya
2015.
Prediction in a Poisson cluster model with multiple cluster processes.
Scandinavian Actuarial Journal,
Vol. 2015,
Issue. 1,
p.
1.
Pang, Guodong
and
Zhou, Yuhang
2018.
Functional limit theorems for a new class of non-stationary shot noise processes.
Stochastic Processes and their Applications,
Vol. 128,
Issue. 2,
p.
505.
Tillier, C.
2018.
Nonparametric Statistics.
Vol. 250,
Issue. ,
p.
171.
Pang, Guodong
and
Taqqu, Murad S.
2019.
Nonstationary self‐similar Gaussian processes as scaling limits of power‐law shot noise processes and generalizations of fractional Brownian motion.
High Frequency,
Vol. 2,
Issue. 2,
p.
95.
Chen, Yiqing
2019.
A Renewal Shot Noise Process with Subexponential Shot Marks.
Risks,
Vol. 7,
Issue. 2,
p.
63.
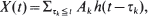 , where {τ k} are the points of a renewal process and {Ak} are i.i.d. with d.f. having a regularly varying tail, the limiting behavior of the maximum is determined. The extremal index is computed and any value in (0, 1) is possible. Two-dimensional point processes of the form
, where {τ k} are the points of a renewal process and {Ak} are i.i.d. with d.f. having a regularly varying tail, the limiting behavior of the maximum is determined. The extremal index is computed and any value in (0, 1) is possible. Two-dimensional point processes of the form 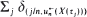 are shown to converge to a compound Poisson point process limit. As a corollary to this result, the joint limiting distribution of high local maxima is obtained.
are shown to converge to a compound Poisson point process limit. As a corollary to this result, the joint limiting distribution of high local maxima is obtained.

