No CrossRef data available.
Article contents
Exponential control of the trajectories of iterated function systems with application to semi-strong GARCH 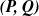 $\boldsymbol{{(P, Q)}}$ models
$\boldsymbol{{(P, Q)}}$ models
Published online by Cambridge University Press: 15 May 2023
Abstract
We establish new results on the strictly stationary solution to an iterated function system. When the driving sequence is stationary and ergodic, though not independent, the strictly stationary solution may admit no moment but we show an exponential control of the trajectories. We exploit these results to prove, under mild conditions, the consistency of the quasi-maximum likelihood estimator of GARCH(p,q) models with non-independent innovations.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
Berkes, I., Horváth, L. and Kokoszka, P. (2003). GARCH processes: Structure and estimation. Bernoulli 9, 201–227.CrossRefGoogle Scholar
Bougerol, P. (1993). Kalman filtering with random coefficients and contractions. SIAM J. Control Optimization 31, 942–959.Google Scholar
Bougerol, P. and Picard, N. (1992). Stationarity of GARCH processes and of some nonnegative time series. J. Econometrics 52, 115–127.Google Scholar
Bougerol, P. and Picard, N. (1992). Strict stationarity of generalized autoregressive processes. Ann. Prob. 20, 1714–1730.CrossRefGoogle Scholar
Brandt, A. (1986). The stochastic equation
 $Y_{n+1} =A_nY_n+B_n$
with stationary coefficients. Adv. Appl. Prob. 18, 211–220.Google Scholar
$Y_{n+1} =A_nY_n+B_n$
with stationary coefficients. Adv. Appl. Prob. 18, 211–220.Google Scholar
Buraczewski, D., Damek, E. and Mikosch, T. (2016). Stochastic Models with Power-Law Tails. Springer, New York.Google Scholar
Elton, J. H. (1990). A multiplicative ergodic theorem for Lipschitz maps. Stoch. Process. Appl. 34, 39–47.Google Scholar
Engle, R. F., Ghysels, E. and Sohn, B. (2013). Stock market volatility and macroeconomic fundamentals. Rev. Econom. Statist. 95, 776–797.Google Scholar
Escanciano, J. C. (2009). Quasi-maximum likelihood estimation of semi-strong GARCH models. Econometric Theory 25, 561–570.Google Scholar
Francq, C., Kandji, B. M. and Zakoian, J.-M. (2023). Inference on multiplicative component GARCH without any small-order moment. Submitted.Google Scholar
Francq, C. and Thieu, L. Q. (2019). QML Inference for volatility models with covariates. Econometric Theory 35, 37–72.Google Scholar
Francq, C., Wintenberger, O. and Zakoian, J.-M. (2018). Goodness-of-fit tests for Log-GARCH and EGARCH models. Test 27, 27–51.CrossRefGoogle Scholar
Francq, C. and Zakoian, J.-M. (2004). Maximum likelihood estimation of pure GARCH and ARMA-GARCH processes. Bernoulli 10, 605–637.Google Scholar
Francq, C. and Zakoian, J.-M. (2007). Quasi-maximum likelihood estimation in GARCH processes when some coefficients are equal to zero. Stoch. Process. Appl. 117, 1265–1284.CrossRefGoogle Scholar
Francq, C. and Zakoian, J.-M. (2019). GARCH Models: Structure, Statistical Inference and Financial Applications. John Wiley, Chichester.CrossRefGoogle Scholar
Han, H. and Kristensen, D. (2014). Asymptotic theory for the QMLE in GARCH-X models with stationary and nonstationary covariates. J. Business Econom. Statist. 32, 416–429.Google Scholar
Jensen, S. T. and Rahbek, A. (2004). Asymptotic inference for nonstationary GARCH. Econometric Theory 20, 1203–1226.Google Scholar
Kesten, H. (1973). Random difference equations and renewal theory for products of random matrices. Acta Math. 131, 207–248.Google Scholar
Lee, S.-W. and Hansen, B. E. (1994). Asymptotic theory for the GARCH(1, 1) quasi-maximum likelihood estimator. Econometric Theory 10, 29–52.CrossRefGoogle Scholar
Straumann, D. and Mikosch, T. (2006). Quasi-maximum-likelihood estimation in conditionally heteroscedastic time series: A stochastic recurrence equations approach. Ann. Statist. 34, 2449–2495.Google Scholar
Tanny, D. (1974). A zero–one law for stationary sequences. Z. Wahrscheinlichkeitsth. 30, 139–148.CrossRefGoogle Scholar



