Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T22:37:09.036Z Has data issue: false hasContentIssue false
  • English
  • Français

The expected number of visits of a sequence of normal partial sums to each side of a boundary

Published online by Cambridge University Press:  14 July 2016

Moshe Pollar
Moshe Pollar*
Affiliation:
The Hebrew University of Jerusalem
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 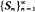be the sequence of partial sums of independent N(μ, 1) random variables. The boundary in the {(n, Sn)} plane which minimizes the expected number of times n that Sn will be below a boundary when μ = θ > 0 subject to a given expected number of visits that Sn will be above the same boundary when μ = 0 is shown to be linear and is also characterized. Similar results are shown for Brownian motion.

Keywords

SUMS OF INDEPENDENT IDENTICALLY DISTRIBUTED RANDOM VARIABLESSTOCHASTIC PROCESSMOVING BOUNDARYBROWNIAN MOTION
Type
Short Communications
Information
Journal of Applied Probability , Volume 15 , Issue 1 , March 1978 , pp. 192 - 198
Copyright
Copyright © Applied Probability Trust 1978 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. II. Wiley, New York.Google Scholar
Luenberger, D. G. (1969) Optimization by Vector Space Methods. Wiley, New York.Google Scholar
Pollar, M. (1978) Optimality and almost optimality of mixture stopping rules. Ann. Statist. To appear.CrossRefGoogle Scholar
Robbins, H. and Siegmund, D. (1970) Boundary crossing probabilities for the Wiener process and sample sums. Ann. Math. Statist. 41, 1410–1429.CrossRefGoogle Scholar
Robbins, H. and Siegmund, D. (1973) Statistical tests of power one and the integral representation of solutions of certain partial differential equations. Bull. Inst. Math. Acad. Sinica 1, 93–120.Google Scholar