Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T10:03:46.366Z Has data issue: false hasContentIssue false
  • English
  • Français

Exact and limiting distributions of the number of lead positions in “unconditional” ballot problems

Published online by Cambridge University Press:  14 July 2016

Ora Engelberg
Ora Engelberg*
Affiliation:
Columbia University, New York.
Get access Rights & Permissions [Opens in a new window]

Extract

In a ballot, candidate A scores a votes and candidate B scores b votes. Suppose the ballots are drawn out one at a time, and denote αr and βr the number of votes registered for A and B, respectively, among the first r votes recorded. Further, let Δa,b be the number of subscripts r satisfying the strict lead condition 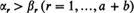, let 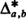be the number of subscripts r satisfying the weak lead condition 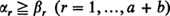; and suppose all possible (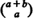) voting records are equally probable. The probability distributions of the number of strict and weak lead positions corresponding to 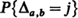and 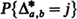, respectively, have been determined in [4] for a≧b.

Type
Short Communications
Information
Journal of Applied Probability , Volume 1 , Issue 1 , June 1964 , pp. 168 - 172
Copyright
Copyright © Applied Probability Trust 1964 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Andersen, E. Sparre (1950) On the frequency of positive partial sums of a series of random variables. Mat. Tidsskr. B, 33–35.Google Scholar
[2] Andersen, E. Sparre (1953) On sums of symmetrically dependent random variables. Skand. Aktuartidskr. 36, 123–138.Google Scholar
[3] Chung, K. L. and Feller, W. (1949) Fluctuation in coin tossing. Proc. Nat. Acad. Sci. U.S.A. 35, 605–608.Google Scholar
[4] Engelberg, O. (1963) Generalizations of the ballot problem. Submitted to Zeit. Wahrscheinlichkeitstheorie. Google Scholar
[5] Erdös, P. and Kac, M. (1947) On the number of positive sums of independent random variables. Bull. Amer. Math. Soc. 53, 1011–1020.Google Scholar