Hostname: page-component-5cf477f64f-r2nwp Total loading time: 0 Render date: 2025-04-04T07:25:34.135Z Has data issue: false hasContentIssue false
  • English
  • Français

Estranged facets and k-facets of Gaussian random point sets

Part of: Multivariate analysis General convexity Geometric probability and stochastic geometry Combinatorial probability Polytopes and polyhedra

Published online by Cambridge University Press:  02 April 2025

Brett Leroux Open the ORCID record for Brett Leroux [Opens in a new window]  and
Luis Rademacher
Brett Leroux*
Affiliation:
University of California, Davis
Luis Rademacher*
Affiliation:
University of California, Davis
*
*Postal address: Department of Mathematics, One Shields Avenue, Davis, CA 95616, USA
*Postal address: Department of Mathematics, One Shields Avenue, Davis, CA 95616, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Gaussian random polytopes have received a lot of attention, especially in the case where the dimension is fixed and the number of points goes to infinity. Our focus is on the less-studied case where the dimension goes to infinity and the number of points is proportional to the dimension d. We study several natural quantities associated with Gaussian random polytopes in this setting. First, we show that the expected number of facets is equal to 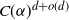$C(\alpha)^{d+o(d)}$, where 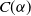$C(\alpha)$ is some constant which depends on the constant of proportionality $\alpha$. We also extend this result to the expected number of k-facets. We then consider the more difficult problem of the asymptotics of the expected number of pairs of estranged facets of a Gaussian random polytope. When the number of points is 2d, we determine the constant C such that the expected number of pairs of estranged facets is equal to 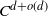$C^{d+o(d)}$.

Keywords

Convex polytopeinner diagonal

MSC classification

Primary: 52A22: Random convex sets and integral geometry 60D05: Geometric probability and stochastic geometry
Secondary: 60C05: Combinatorial probability 62H10: Distribution of statistics 52B05: Combinatorial properties (number of faces, shortest paths, etc.)
Type
Original Article
Information
Journal of Applied Probability , First View , pp. 1 - 17
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Affentranger, F. and Schneider, R. (1992). Random projections of regular simplices. Discrete Comput. Geom. 7, 219–226.Google Scholar
Bárány, I. and Steiger, W. (1994). On the expected number of k-sets. Discrete Comput. Geom. 11, 243–263.Google Scholar
Bárány, I., Vempala, S. and Vetta, A. (2007). Nash equilibria in random games. Random Structures Algorithms 31, 391–405.Google Scholar
Baryshnikov, Y. M. and Vitale, R. A. (1994). Regular simplices and Gaussian samples. Discrete Comput. Geom. 11, 141–147.Google Scholar
Bonnet, G., Grote, J., Temesvari, D., Thäle, C., Turchi, N. and Wespi, F. (2017). Monotonicity of facet numbers of random convex hulls. J. Math. Anal. Appl. 455, 1351–1364.CrossRefGoogle Scholar
Bonnet, G. and O’Reilly, E. (2022). Facets of spherical random polytopes. Math. Nachr. 295, 1901–1933.Google Scholar
Böröczky, K. J., Lugosi, G. and Reitzner, M. (2024). Facets of high-dimensional Gaussian polytopes. J. Geom. Anal. 34, 69.Google Scholar
Brascamp, H. J. and Lieb, E. H. (1976). On extensions of the Brunn–Minkowski and Prékopa–Leindler theorems, including inequalities for log concave functions, and with an application to the diffusion equation. J. Funct. Anal. 22, 366–389.Google Scholar
Brazitikos, S., Giannopoulos, A., Valettas, P. and Vritsiou, B.-H. (2014). Geometry of Isotropic Convex Bodies (Math. Surveys Monographs 196). American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
Bremner, D. and Klee, V. (1999). Inner diagonals of convex polytopes. J. Combinatorial Theory A 87, 175–197.CrossRefGoogle Scholar
Clarkson, K. L. (2004). On the expected number of k-sets of coordinate-wise independent points. Preprint, available at https://kenclarkson.org/cwi_ksets/p.pdf.Google Scholar
Cover, T. M. and Thomas, J. A. (2006). Elements of Information Theory, 2nd edn. John Wiley, New York.Google Scholar
Erdös, P., Lovász, L., Simmons, A. and Straus, E. G. (1973). Dissection graphs of planar point sets. In A Survey of Combinatorial Theory, ed. J. N. Srivastava. Springer, New York, pp. 139–149.Google Scholar
Fleury, B. (2012). Poincaré inequality in mean value for Gaussian polytopes. Prob. Theory Relat. Fields 152, 141–178.Google Scholar
Hug, D., Munsonius, G. O. and Reitzner, M. (2004). Asymptotic mean values of Gaussian polytopes. Beiträge Algebra Geom. 45, 531–548.Google Scholar
Hug, D. and Reitzner, M. (2005). Gaussian polytopes: Variances and limit theorems. Adv. Appl. Prob. 37, 297–320.Google Scholar
Klee, V. and Walkup, D. W. (1967). The d-step conjecture for polyhedra of dimension $d<6$ . Acta Math. 117, 53–78.Google Scholar
Leroux, B. and Rademacher, L. (2023). Improved bounds for the expected number of k-sets. Discrete Comput. Geom. 70, 790–815.Google Scholar
Loera, J. A. D., Haddock, J. and Rademacher, L. (2020). The minimum Euclidean-norm point in a convex polytope: Wolfe’s combinatorial algorithm is exponential. SIAM J. Comput. 49, 138–169.CrossRefGoogle Scholar
Lovász, L. (1971). On the number of halving lines. Ann. Univ. Sci. Budapest, Etovos, Sect. Math. 14, 107–108.Google Scholar
Lovász, L. and Vempala, S. (2007). The geometry of logconcave functions and sampling algorithms. Random Structures Algorithms 30, 307–358.CrossRefGoogle Scholar
Miles, R. E. (1971). Isotropic random simplices. Adv. Appl. Prob. 3, 353–382.CrossRefGoogle Scholar
Rademacher, L. (2012). On the monotonicity of the expected volume of a random simplex. Mathematika 58, 77–91.CrossRefGoogle Scholar
Raynaud, H. (1970). Sur l’enveloppe convexe des nuages de points aléatoires dans $R^{n}$ . I. J. Appl. Prob. 7, 35–48.Google Scholar
Rényi, A. and Sulanke, R. (1963). Über die konvexe Hülle von n zufällig gewählten Punkten. Z. Wahrscheinlichkeitsth. 2, 75–84.CrossRefGoogle Scholar
Rudin, W. (1987). Real and Complex Analysis, 3rd edn. McGraw-Hill Book Co., New York.Google Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.CrossRefGoogle Scholar
von Stengel, B. (1999). New maximal numbers of equilibria in bimatrix games. Discrete Comput. Geom. 21, 557–568.CrossRefGoogle Scholar
Wagner, U. (2008). k-sets and k-facets. In Surveys on Discrete and Computational Geometry (Contemp. Math. 453), eds J. E. Goodman, J. Pach and R. Pollack. Americal Mathematical Society, Providence, RI, pp. 443–513.CrossRefGoogle Scholar