Published online by Cambridge University Press: 14 July 2016
Particles enter a finite-state system and move according to independent sample paths from a semi-Markov process. Strong limit theorems are developed for the ratio of the flow of particles from states i to j and the flow out of 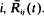 When the cumulative arrival of particles into the system up to time t, A (t) ∼ λtα, then
When the cumulative arrival of particles into the system up to time t, A (t) ∼ λtα, then 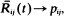 a.s. When A (t)∼ λekt, then the flow between states must be normalized by
a.s. When A (t)∼ λekt, then the flow between states must be normalized by 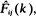 the Laplace–Stieltjes transform of the conditional holding time distribution, in order to make the ratio an unbiased estimator of ρij.
the Laplace–Stieltjes transform of the conditional holding time distribution, in order to make the ratio an unbiased estimator of ρij.