Published online by Cambridge University Press: 30 March 2016
Let f be an integrable function on an infinite measure space (S, 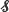 , π). We show that if a regenerative sequence {Xn}n≥0 with canonical measure π could be generated then a consistent estimator of λ ≡ ∫Sf dπ can be produced. We further show that under appropriate second moment conditions, a confidence interval for λ can also be derived. This is illustrated with estimating countable sums and integrals with respect to absolutely continuous measures on ℝd using a simple symmetric random walk on ℤ.
, π). We show that if a regenerative sequence {Xn}n≥0 with canonical measure π could be generated then a consistent estimator of λ ≡ ∫Sf dπ can be produced. We further show that under appropriate second moment conditions, a confidence interval for λ can also be derived. This is illustrated with estimating countable sums and integrals with respect to absolutely continuous measures on ℝd using a simple symmetric random walk on ℤ.