Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T18:10:59.406Z Has data issue: false hasContentIssue false
  • English
  • Français

Empirical Laplace transform and approximation of compound distributions

Published online by Cambridge University Press:  14 July 2016

Sándor Csörgő  and
Jef L. Teugels
Sándor Csörgő*
Affiliation:
Szeged University
Jef L. Teugels*
Affiliation:
Katholieke Universiteit Leuven
*
∗Postal address: Bolyai Intezete, Szeged University, H-6720 Szeged, Aradi vértanúk tere 1, Hungary.
∗∗Postal address: Department of Mathematics, Katholieke Universiteit Leuven, Celestijnenlaan 200B, B-3030 Leuven, Belgium.
Get access Rights & Permissions [Opens in a new window]

Abstract

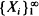Let be i.i.d. non-negative random variables with d.f. F and Laplace transform L. Let N be integer valued and independent of 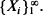In many applications one knows that for y → ∞ and a function φ 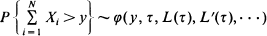where in turn τ is the solution of an equation 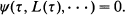On the basis of a sample of size n we derive an estimator τ n for τ by solving ψ (τ n, Ln(τ n), L′n(τ n), · ··) = 0 where Ln is the empirical version of L. This estimator is then used to derive the asymptotic behaviour of φ (y, τ n, Ln(τ n), L′n(τ n), · ··). We include five examples, some of which are taken from insurance mathematics.

Keywords

PROBABILITY OF RUININSURANCE MATHEMATICS
Type
Research Papers
Information
Journal of Applied Probability , Volume 27 , Issue 1 , March 1990 , pp. 88 - 101
Copyright
Copyright © Applied Probability Trust 1990 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Work partially supported by the Hungarian National Foundation for Scientific Research, Grants 1808/86 and 457/88.

References

Beekman, J. A. (1974) Two Stochastic Processes. Almquist & Wiksell, Stockholm.Google Scholar
Buhlmann, H. (1970) Mathematical Methods of Risk Theory. Springer-Verlag, Berlin.Google Scholar
Csörgo, S. (1982) The empirical moment generating function. Coll. Math. Soc. J. Bolyai, 32, Nonparametric Statistical Inference, ed. Gnedenko, B. V., Puri, M. L. and Vincze, I., Elsevier, Amsterdam, 139–150.Google Scholar
Embrechts, P., Maejima, M. and Teugels, J. L. (1985a) Asymptotic behaviour of compound distributions. Astin Bulletin 15, 45–48.CrossRefGoogle Scholar
Embrechts, P., Jensen, J. L., Maejima, M. and Teugels, J. L. (1985b) Approximations for compound Poisson and Pólya processes. Adv. Appl. Prob. 17, 623–637.Google Scholar
Feller, W. (1971) An Introduction to Probability Theory and its Applications, Vol. II, 2nd edn. Wiley, New York.Google Scholar
Serfling, R. J. (1980) Approximation Theorems of Mathematical Statistics. Wiley, New York.CrossRefGoogle Scholar
Sundt, B. (1982) Asymptotic behaviour of compound distributions and stop loss premiums. Astin Bulletin 13, 89–98.Google Scholar
Takács, L. (1967) Combinatorial Methods in the Theory of Stochastic Processes. Wiley, New York.Google Scholar
Teugels, J. L. (1985) Approximation and estimation of some compound distributions. Insurance: Math. & Econ. 4, 143–153.Google Scholar