Published online by Cambridge University Press: 14 July 2016
Birth and death processes, i.e. Markov chains {X(t)}, 0 ≦ t ≦ ∞, taking values in the set I of non-negative integers, for which the infinitesimal transition probabilities are
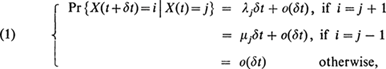 have found wide application in mathematical ecology . In order that the infinite system of differential Equations (1) should have solutions
have found wide application in mathematical ecology . In order that the infinite system of differential Equations (1) should have solutions
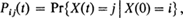 such that Pij(t) ≦ 0, all t and
such that Pij(t) ≦ 0, all t and
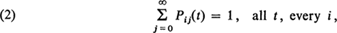 it is necessary and sufficient that
it is necessary and sufficient that
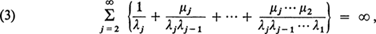 . The conditions ensure that with probability one, the sample paths of X(t) have no discontinuities worse than jumps, and in this case the solution is unique. If (3) does not hold then for some t1 at least, there is a set of sample paths of positive probability, each of which has t1 as a limit point of jumps. For pure birth processes, (in which μj = 0) this clearly implies X(t) → ∞ as t → t1.
. The conditions ensure that with probability one, the sample paths of X(t) have no discontinuities worse than jumps, and in this case the solution is unique. If (3) does not hold then for some t1 at least, there is a set of sample paths of positive probability, each of which has t1 as a limit point of jumps. For pure birth processes, (in which μj = 0) this clearly implies X(t) → ∞ as t → t1.