Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T19:27:11.988Z Has data issue: false hasContentIssue false
  • English
  • Français

The density of interfaces: a new first-passage problem

Part of: Special processes Equilibrium statistical mechanics

Published online by Cambridge University Press:  14 July 2016

L. Chayes  and
C. Winfield
L. Chayes
Affiliation:
University of California, Los Angeles
C. Winfield*
Affiliation:
University of California, Los Angeles
*
∗ Postal address for both authors: Department of Mathematics, University of California, Los Angeles, CA 90024, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce and study a novel type of first-passage percolation problem on 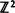where the associated first-passage time measures the density of interface between two types of sites. If the types, designated + and –, are independently assigned their values with probability p and (1 — p) respectively, we show that the density of interface is non-zero provided that both species are subcritical with regard to percolation, i.e. pc > p > 1 – pc. Furthermore, we show that as p ↑ pc or p ↓ (1 – pc), the interface density vanishes with scaling behavior identical to the correlation length of the site percolation problem.

Keywords

PERCOLATIONFIRST-PASSAGE PERCOLATION

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 82B41: Random walks, random surfaces, lattice animals, etc. 82B43: Percolation 82B44: Disordered systems (random Ising models, random Schrödinger operators, etc.)
Type
Research Papers
Information
Journal of Applied Probability , Volume 30 , Issue 4 , December 1993 , pp. 851 - 862
Copyright
Copyright © Applied Probability Trust 1993 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, D. B. and Newman, C. M. (1988) Wetting in a three-dimensional system: an exact solution. Phys. Rev. Lett. 61, 1969–1972.Google Scholar
Abraham, D. B., Chayes, J. T. and Chayes, L. (1984) Unpublished results.Google Scholar
Aizenman, M., Chayes, J. T., Chayes, L., Fröhlich, J. and Russo, L. (1983) On a sharp transition, from area law to perimeter law in a system of random surfaces. Commun. Math. Phys. 92, 19–69.Google Scholar
Campanino, M. and Russo, L. (1985) An upper bound on the critical probability for the three-dimensional cubic lattice. Ann. Prob. 13, 478–491.CrossRefGoogle Scholar
Chayes, J. T. and Chayes, L. (1986) Percolation and random media. In Critical Phenomena, Random Systems and Gauge Theories, Part II. Les Houches Session XLIII 1984 , ed. Osterwalder, K. and Stora, R. North-Holland, Amsterdam.Google Scholar
Chayes, J. T., Chayes, L. and Durrett, R. (1986) Critical behavior of the two-dimensional first passage time. J. Statist. Phys. 45, 933–951.Google Scholar
Chayes, L. (1991) On the critical behavior of the first passage time in d 3. Helv. Phys. Acta 64, 1055–1069.Google Scholar
Chayes, L. (1993) The density of Peierls contours and the height of the wedding cake. J. Phys. A. Math. Gen.Google Scholar
Durrett, R. (1988) Lecture Notes on Particle Systems and Percolation, Wadsworth & Brooks/Cole, Belmont, CA.Google Scholar
Fontes, L. and Newman, C. M. (1993) First passage percolation for random colorings of. Preprint.Google Scholar
Hammersley, J. M. and Welsh, D. J. A. (1965) First passage percolation, subadditive processes, stochastic networks and generalized renewal theory. In Bernoulli-Bayes-Laplace Anniversary Volume, ed. Neyman, J. and LeCam, L. M., Springer-Verlag, Berlin.Google Scholar
Higuchi, Y. (1982) Coexistence of the infinite* clusters; a remark on the square lattice percolation. Z. Wahrscheinlichkeitsth. 61, 75–81.Google Scholar
Kesten, H. (1982) Percolation Theory for Mathematicians. Progress in Probability and Statistics Vol. 2, Birkhäuser, Basel.Google Scholar
Kesten, H. (1986) Aspects of First Passage Percolation. Lecture Notes in Mathematics 1180, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Kingman, J. F. C. (1968) The ergodic theory of subadditive stochastic processes. J. R. Statist. Soc. B30, 499–510.Google Scholar
Russo, L. (1981) On the critical percolation probabilities. Z. Wahrscheinlichkeitsth. 56, 229–237.CrossRefGoogle Scholar
Smythe, R. T. and Wierman, J. C. (1978) First passage percolation on the square lattice. Lecture Notes in Mathematics 671, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Whitney, H. (1933) Planar graphs. Fund. Math. 21, 73–84.Google Scholar