Published online by Cambridge University Press: 15 November 2022
We consider a Lévy process Y(t) that is not continuously observed, but rather inspected at Poisson(
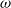 $\omega$
) moments only, over an exponentially distributed time
$\omega$
) moments only, over an exponentially distributed time
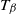 $T_\beta$
with parameter
$T_\beta$
with parameter
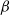 $\beta$
. The focus lies on the analysis of the distribution of the running maximum at such inspection moments up to
$\beta$
. The focus lies on the analysis of the distribution of the running maximum at such inspection moments up to
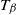 $T_\beta$
, denoted by
$T_\beta$
, denoted by
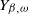 $Y_{\beta,\omega}$
. Our main result is a decomposition: we derive a remarkable distributional equality that contains
$Y_{\beta,\omega}$
. Our main result is a decomposition: we derive a remarkable distributional equality that contains
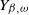 $Y_{\beta,\omega}$
as well as the running maximum process
$Y_{\beta,\omega}$
as well as the running maximum process
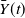 $\bar Y(t)$
at the exponentially distributed times
$\bar Y(t)$
at the exponentially distributed times
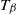 $T_\beta$
and
$T_\beta$
and
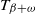 $T_{\beta+\omega}$
. Concretely,
$T_{\beta+\omega}$
. Concretely,
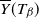 $\overline{Y}(T_\beta)$
can be written as the sum of two independent random variables that are distributed as
$\overline{Y}(T_\beta)$
can be written as the sum of two independent random variables that are distributed as
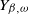 $Y_{\beta,\omega}$
and
$Y_{\beta,\omega}$
and
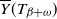 $\overline{Y}(T_{\beta+\omega})$
. The distribution of
$\overline{Y}(T_{\beta+\omega})$
. The distribution of
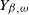 $Y_{\beta,\omega}$
can be identified more explicitly in the two special cases of a spectrally positive and a spectrally negative Lévy process. As an illustrative example of the potential of our results, we show how to determine the asymptotic behavior of the bankruptcy probability in the Cramér–Lundberg insurance risk model.
$Y_{\beta,\omega}$
can be identified more explicitly in the two special cases of a spectrally positive and a spectrally negative Lévy process. As an illustrative example of the potential of our results, we show how to determine the asymptotic behavior of the bankruptcy probability in the Cramér–Lundberg insurance risk model.