Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T18:38:07.486Z Has data issue: false hasContentIssue false
  • English
  • Français

A cost relationship between age and block replacement policies

Published online by Cambridge University Press:  14 July 2016

Thomas H. Savits
Thomas H. Savits*
Affiliation:
University of Pittsburgh
*
∗Postal address: Department of Mathematics and Statistics, University of Pittsburgh, Pittsburgh, PA 15260, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

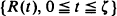The general cost structure of a unit on line is assumed to be governed by a stochastic process , where R(t) denotes the operating cost on [0, t)and ζ denotes the time of an unscheduled (or unplanned) replacement by a new unit at a cost c1. For an age replacement maintenance policy, scheduled (or planned) replacements occur whenever an operating unit reaches age T, whereas in the block replacement case, scheduled replacements occur every T units of time. Such scheduled replacements cost c2. The expected long-run cost per unit time can then be expressed in the form A(T)/Ε [min(ζ, T)] and B(T)/T respectively. Our main result shows that 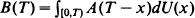where U is the associated renewal function generated by ζ.

Keywords

MINIMAL REPAIRRENEWAL REWARDNON-HOMOGENEOUS POISSON PROCESS
Type
Research Papers
Information
Journal of Applied Probability , Volume 25 , Issue 4 , December 1988 , pp. 789 - 796
Copyright
Copyright © Applied Probability Trust 1988 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by ONR Contract N0014–84-K-0084 and AFOSR Grant AFOSR-84–0113.

References

Abdel-Hameed, M. (1985) An imperfect maintenance model with block replacements. Kuwait University Technical Report No. 21.Google Scholar
Barlow, R. E. and Proschan, F. (1965) Mathematical Theory of Reliability. Wiley, New York.Google Scholar
Beichelt, F. (1976) A general preventive maintenance policy. Math. Operationsforsch, u. Statist. 7, 927–932.Google Scholar
Berg, M. and Cleroux, R. (1982) The block replacement problem with minimal repair and random repair costs. J. Statist. Comp. Simul. 15, 1–7.Google Scholar
Berg, M., Bienvenu, M. and Cleroux, R. (1986) Age replacement policy with age-dependent minimal repair. Infor 24, 26–32.Google Scholar
Block, H. W. and Savits, T. H. (1987) Block replacement for a general model with minimal repair. University of Pittsburgh Technical Report.Google Scholar
Block, H. W., Borges, W. S. and Savits, T. H. (1983) A general minimal repair maintenance model. University of Pittsburgh, Technical Report No. 83–17.Google Scholar
Block, H. W., Borges, W. S. and Savits, T. H. (1986) Preventive maintenance policies. In Reliability and Quality Control , ed. Basu, A. P., Elsevier, North-Holland, Amsterdam, 101–106.Google Scholar
Boland, P. J. and Proschan, F. (1982) Periodic replacement with increasing minimal repair costs at failure. Operat. Res. 30, 1183–1189.Google Scholar
Boland, P. J. and Proschan, F. (1983) Optimum replacement of a system subject to shocks. Operat. Res. 31, 697–704.CrossRefGoogle Scholar
Cleroux, R., Dubuc, S. and Tilquin, C. (1979) The age replacement problem with minimal repair and random repair costs. Operat. Res. 27, 1158–1167.CrossRefGoogle Scholar
Feller, W. (1966) An Introduction to Probability Theory and Its Applications. Vol. II. Wiley, New York.Google Scholar
Puri, P. S. and Singh, H. (1986) Optimum replacement of a system subject to shocks: a mathematical lemma. Operat. Res. 34, 782–789.Google Scholar
Ross, S. M. (1970) Applied Probability Models with Optimization Applications. Holden-Day, San Francisco.Google Scholar