Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-25T17:30:39.073Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent distributions on the square–extreme points and asymptotics

Part of: Distribution theory - Probability

Published online by Cambridge University Press:  05 April 2024

Stanisław Cichomski  and
Adam Osękowski
Stanisław Cichomski*
Affiliation:
University of Warsaw
Adam Osękowski*
Affiliation:
University of Warsaw
*
*Postal address: Faculty of Mathematics (MIMUW), Banacha 2, 02-097, Warsaw, Poland.
*Postal address: Faculty of Mathematics (MIMUW), Banacha 2, 02-097, Warsaw, Poland.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 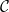$\mathcal{C}$ denote the family of all coherent distributions on the unit square 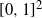$[0,1]^2$, i.e. all those probability measures 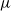$\mu$ for which there exists a random vector 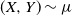$(X,Y)\sim \mu$, a pair 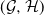$(\mathcal{G},\mathcal{H})$ of 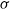$\sigma$-fields, and an event E such that 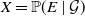$X=\mathbb{P}(E\mid\mathcal{G})$, 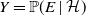$Y=\mathbb{P}(E\mid\mathcal{H})$ almost surely. We examine the set 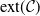$\mathrm{ext}(\mathcal{C})$ of extreme points of 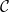$\mathcal{C}$ and provide its general characterisation. Moreover, we establish several structural properties of finitely-supported elements of 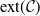$\mathrm{ext}(\mathcal{C})$. We apply these results to obtain the asymptotic sharp bound 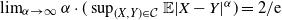$\lim_{\alpha \to \infty}\alpha\cdot(\sup_{(X,Y)\in \mathcal{C}}\mathbb{E}|X-Y|^{\alpha}) = {2}/{\mathrm{e}}$.

Keywords

Conditional probabilityexperts opinionsjoint distribution of conditional expectations

MSC classification

Primary: 60E05: Distributions
Secondary: 60E15: Inequalities; stochastic orderings
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 4 , December 2024 , pp. 1240 - 1262
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arieli, I. and Babichenko, Y. (2024). A population’s feasible posterior beliefs. J. Econom. Theory 215, 105764.CrossRefGoogle Scholar
Arieli, I., Babichenko, Y. and Sandomirskiy, F. (2022). Persuasion as transportation. Preprint. Available at https://doi.org/10.48550/arXiv.2307.07672.Google Scholar
Arieli, I., Babichenko, Y., Sandomirskiy, F. and Tamuz, O. (2021). Feasible joint posterior beliefs. J. Political Econom. 129, 2546–2594.CrossRefGoogle Scholar
Boza, S., Kr̆epela, M. and Soria, J. (2022). Lorentz and Gale–Ryser theorems on general measure spaces. Proc. R. Soc. Edinburgh A 152, 857–878.CrossRefGoogle Scholar
Burdzy, K. and Pal, S. (2021). Can coherent predictions be contradictory? Adv. Appl. Prob. 53, 133–161.CrossRefGoogle Scholar
Burdzy, K. and Pitman, J. (2020). Bounds on the probability of radically different opinions. Electron. Commun. Prob. 25, 1–12.CrossRefGoogle Scholar
Cichomski, S. (2020). Maximal spread of coherent distributions: A geometric and combinatorial perspective. Master’s thesis, University of Warsaw. Available at https://doi.org/10.48550/arXiv.2007.08022.CrossRefGoogle Scholar
Cichomski, S. and OsĘkowski, A. (2021). The maximal difference among expert’s opinions. Electron. J. Prob. 26, 1–17.CrossRefGoogle Scholar
Cichomski, S. and OsĘkowski, A. (2022). Contradictory predictions with multiple agents. Preprint. Available at https://doi.org/10.48550/arXiv.2211.02446.Google Scholar
Cichomski, S. and OsĘkowski, A. (2023) Doob’s estimate for coherent random variables and maximal operators on trees. Prob. Math. Statist. 43, 109–119.CrossRefGoogle Scholar
Cichomski, S. and Petrov, F. (2023). A combinatorial proof of the Burdzy–Pitman conjecture. Electron. Commun. Prob. 28, 1–7.CrossRefGoogle Scholar
Dawid, A. P., DeGroot, M. H. and Mortera, J. (1995). Coherent combination of experts’ opinions. Test 4, 263–313.CrossRefGoogle Scholar
DeGroot, M. H. (1988). A Bayesian view of assessing uncertainty and comparing expert opinion. J. Statist. Planning Infer. 20, 295–306.CrossRefGoogle Scholar
Dubins, L. E. and Schwarz, G. (1967). On extremal martingale distributions. In Proc. 5th Berkeley Symp. Math. Statist. Prob., Vol. II, University of California Press, Berkeley, pp. 295–299.Google Scholar
He, K., Sandomirskiy, F. and Tamuz, O. (2022). Private private information. Preprint. Available at https://doi.org/10.48550/arXiv.2112.14356.Google Scholar
Hestir, K. and Williams, S. C. (1995). Supports of doubly stochastic measures. Bernoulli 1, 217–243.CrossRefGoogle Scholar
Ranjan, R. and Gneiting, T. (2010). Combining probability forecasts. J. R. Statist. Soc. Ser. B 72, 71–91.CrossRefGoogle Scholar
Rudin, W. (1991). Functional Analysis, 2nd edn. McGraw-Hill, New York.Google Scholar
Satopää, V. A., Pemantle, R. and Ungar, L. H. (2016) Modeling probability forecasts via information diversity. J. Amer. Statist. Assoc. 111, 1623–1633.CrossRefGoogle Scholar
Tao, T. (2006). Szemerédi’s regularity lemma revisited. Contrib. Discrete Math. 1, 8–28.Google Scholar
Zhu, T. (2022). Some problems on the convex geometry of probability measures. PhD thesis, University of California, Berkeley.Google Scholar