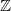Hostname: page-component-5cf477f64f-bmd9x Total loading time: 0 Render date: 2025-04-08T02:40:52.982Z Has data issue: false hasContentIssue false
  • English
  • Français

Coexistence of lazy frogs on ${\mathbb{Z}}$

Part of: Markov processes Special processes

Published online by Cambridge University Press:  28 June 2022

Mark Holmes Open the ORCID record for Mark Holmes [Opens in a new window]  and
Daniel Kious
Mark Holmes*
Affiliation:
University of Melbourne
Daniel Kious*
Affiliation:
University of Bath
*
*Postal address: School of Mathematics and Statistics, The University of Melbourne, Parkville, VIC 3010, Australia. Email: [email protected]
**Postal address: Department of Mathematical Sciences, The University of Bath, Claverton Down, Bath, BA2 7AY. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the so-called frog model on 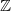${\mathbb{Z}}$ with two types of lazy frogs, with parameters 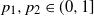$p_1,p_2\in (0,1]$ respectively, and a finite expected number of dormant frogs per site. We show that for any such 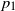$p_1$ and 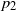$p_2$ there is positive probability that the two types coexist (i.e. that both types activate infinitely many frogs). This answers a question of Deijfen, Hirscher, and Lopes in dimension one.

Keywords

Frog modelcoexistencerandom walkcompeting growth

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory 60K37: Processes in random environments
Secondary: 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 3 , September 2022 , pp. 702 - 713
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, O. S. M., Machado, F. P. and Popov, S. Yu. (2002). The shape theorem for the frog model. Ann. Appl. Prob. 12, 533–546.10.1214/aoap/1026915614CrossRefGoogle Scholar
Alves, O. S. M., Machado, F. P., Popov, S. Yu. and Ravishankar, K. (2001). The shape theorem for the frog model with random initial configuration. Markov Proc. Relat. Fields 7, 525–539.Google Scholar
Deijfen, M. and Häggström, O. (2008). The pleasures and pains of studying the two-type Richardson model. In Analysis and Stochastics of Growth Processes and Interface Models, eds P. Mörters, R. Moser, M. Penrose, H. Schwetlick and J. Zimmer, Oxford Scholarship Online.10.1093/acprof:oso/9780199239252.003.0002CrossRefGoogle Scholar
Deijfen, M., Hirscher, T. and Lopes, F. (2019). Competing frogs on ${\mathbb{Z}}^d$ . Electron. J. Prob. 24, 1–17.10.1214/19-EJP400CrossRefGoogle Scholar
Deijfen, M. and Rosengren, S. (2019). The initial set in the frog model is irrelevant. Preprint, arXiv:1912.10085.Google Scholar
Finn, T. and Stauffer, A. (2020). Non-equilibrium multi-scale analysis and coexistence in competing first passage percolation. Preprint, arXiv:2009.05463.Google Scholar
Rolla, L. T. (2015). Activated random walks. Preprint, arXiv:1507.04341.Google Scholar
Shi, Z. (2015). Branching Random Walks (Lect. Notes Math. 2151). Springer, New York.Google Scholar
Telcs, A. and Wormald, N. C. (1999). Branching and tree indexed random walks on fractals. J. Appl. Prob. 36, 999–1011.10.1239/jap/1032374750CrossRefGoogle Scholar