Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T14:04:53.161Z Has data issue: false hasContentIssue false
  • English
  • Français

A Central Limit Theorem Associated with the Transformed Two-Parameter Poisson–Dirichlet Distribution

Part of: Limit theorems

Published online by Cambridge University Press:  14 July 2016

Fang Xu
Fang Xu*
Affiliation:
Beijing Normal University and McMaster University
*
∗Postal address: Department of Mathematics and Statistics, McMaster University, 1280 Main Street West, Hamilton, Ontario, Canada L8S 4K1. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we introduce the transformed two-parameter Poisson–Dirichlet distribution 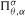on the ordered infinite simplex. Furthermore, we prove the central limit theorem related to this distribution when both the mutation rate θ and the selection rate σ become large in a specified manner. As a consequence, we find that the properly scaled homozygosities have asymptotical normal behavior. In particular, there is a certain phase transition with the limit depending on the relative strength of σ and θ.

Keywords

Poisson–Dirichlet distributiontwo-parameter Poisson–Dirichlet distributionhomozygosityGEM representationselection

MSC classification

Secondary: 60F05: Central limit and other weak theorems 92D10: Genetics
Type
Research Article
Information
Journal of Applied Probability , Volume 46 , Issue 2 , June 2009 , pp. 392 - 401
Copyright
Copyright © Applied Probability Trust 2009 

References

[1] Dawson, D. A. and Feng, S. (2006). Asymptotic behavior of the Poisson–Dirichlet distribution for large mutation rate. Ann. Appl. Prob. 16, 562–582.Google Scholar
[2] Ethier, S. N. and Kurtz, T. G. (1994). Convergence to Fleming–Viot processes in the weak atomic topology. Stoch. Process. Appl. 54, 1–27.Google Scholar
[3] Feng, S. (2007). Large deviations for Dirichlet processes and Poisson–Dirichlet distribution with two parameters. Electron. J. Prob. 12, 787–807.Google Scholar
[4] Griffiths, R. C. (1979). On the distribution of allele frequencies in a diffusion model. Theoret. Pop. Biol. 15, 140–158.Google Scholar
[5] Joyce, P., Krone, S. M. and Kurtz, T. G. (2002). Gaussian limits associated with the Poisson–Dirichlet distribution and the Ewens sampling formula. Ann. Appl. Prob. 12, 101–124.Google Scholar
[6] Joyce, P., Krone, S. M. and Kurtz, T. G. (2003). When can one detect overdominant selection in the infinite-alleles model? Ann. Appl. Prob. 13, 181–212.Google Scholar
[7] Kenji, H. (2009). The two-parameter Poisson–Dirichlet point process. To appear in Bernoulli. Google Scholar
[8] Kingman, J. F. C. (1977). The population structure associated with the Ewens sampling formula. Theoret. Pop. Biol. 11, 274–283.Google Scholar
[9] Kingman, J. F. C. et al. (1975). Random discrete distributions. J. R. Statist. Soc. B 37, 1–22.Google Scholar
[10] Pitman, J. (1992). The two-parameter generalization of Ewens' random partition structure. Tech. Rep. 345, Department of Statistics, University of California, Berkeley.Google Scholar
[11] Pitman, J. (1995). Exchangeable and partially exchangeable random partitions. Prob. Theory Relat. Fields 102, 145–158.CrossRefGoogle Scholar
[12] Pitman, J. and Yor, M. (1997). The two-parameter Poisson–Dirichlet distribution derived from a stable subordinator. Ann. Prob. 25, 855–900.Google Scholar