Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-25T05:31:54.330Z Has data issue: false hasContentIssue false
  • English
  • Français

A branching random walk in the presence of a hard wall

Part of: Stochastic processes Markov processes

Published online by Cambridge University Press:  22 May 2023

Rishideep Roy Open the ORCID record for Rishideep Roy [Opens in a new window]
Rishideep Roy*
Affiliation:
IIM Bangalore
*
*Postal address: IIM Bangalore, Bannerghatta Road, Bangalore 560076, India. Email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a branching random walk on a d-ary tree of height n (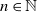$n \in \mathbb{N}$), in the presence of a hard wall which restricts each value to be positive, where d is a natural number satisfying 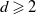$d\geqslant2$. We consider the behaviour of Gaussian processes with long-range interactions, for example the discrete Gaussian free field, under the condition that it is positive on a large subset of vertices. We observe a relation with the expected maximum of the processes. We find the probability of the event that the branching random walk is positive at every vertex in the nth generation, and show that the conditional expectation of the Gaussian variable at a typical vertex, under positivity, is less than the expected maximum by order of 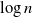$\log n$.

Keywords

Branching random walkextrema of Gaussian processeslog-correlated fieldsentropic repulsion

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.)
Secondary: 60G15: Gaussian processes 60G70: Extreme value theory; extremal processes
Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 1 , March 2024 , pp. 1 - 17
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aïdékon, E. (2013). Convergence in law of the minimum of a branching random walk. Ann. Prob. 41, 1362–1426.CrossRefGoogle Scholar
Bolthausen, E., Deuschel, J.-D. and Giacomin, G. (2001). Entropic repulsion and the maximum of the two-dimensional harmonic crystal. Ann. Prob. 29, 1670–1692.CrossRefGoogle Scholar
Bolthausen, E., Deuschel, J.-D. and Zeitouni, O. (1995). Entropic repulsion of the lattice free field. Commun. Math. Phys. 170, 417–443.CrossRefGoogle Scholar
Bramson, M. and Zeitouni, O. (2011). Tightness of the recentered maximum of the two-dimensional discrete Gaussian free field. Commun. Pure Appl. Math. 65, 1–20.CrossRefGoogle Scholar
Bramson, M., Ding, J. and Zeitouni, O. (2016). Convergence in law of the maximum of the two-dimensional discrete Gaussian free field. Commun. Pure Appl. Math. 69, 62–123.CrossRefGoogle Scholar
Bramson, M., Ding, J. and Zeitouni, O. (2016). Convergence in law of the maximum of nonlattice branching random walk. Ann. Inst. H. Poincaré Prob. Statist. 52, 1897–1924.CrossRefGoogle Scholar
Caputo, P., Martinelli, F. and Toninelli, F. L. (2017). Entropic repulsion in $|\nabla \phi|^p$ surfaces: a large deviation bound for all $p\geq 1$ . Boll. Unione Mat. Ital. 10, 451–466.CrossRefGoogle Scholar
Chen, J. P. and Ugurcan, B. E. (2015). Entropic repulsion of Gaussian free field on high-dimensional Sierpinski carpet graphs. Stoch. Process. Appl. 125, 4632–4673.CrossRefGoogle Scholar
Deuschel, J.-D. (1996). Entropic repulsion of the lattice free field II: the 0-boundary case. Commun. Math. Phys. 181, 647–665.CrossRefGoogle Scholar
Deuschel, J.-D. and Giacomin, G. (1999). Entropic repulsion for the free field: pathwise characterization in $d \geq 3$ . Commun. Math. Phys. 206, 447–462.CrossRefGoogle Scholar
Deuschel, J.-D. and Giacomin, G. (2000). Entropic repulsion for massless fields. Stoch. Process. Appl. 89, 333–354.CrossRefGoogle Scholar
Ding, J. and Goswami, S. (2017). First passage percolation on the exponential of two-dimensional branching random walk. Electron. Commun. Prob. 22, 1–14.CrossRefGoogle Scholar
Ding, J., Roy, R. and Zeitouni, O. (2017). Convergence of the centered maximum of log-correlated Gaussian fields. Ann. Prob. 45, 3886–3928.CrossRefGoogle Scholar
Kurt, N. (2009). Maximum and entropic repulsion for a Gaussian membrane model in the critical dimension. Ann. Prob. 37, 687–725.CrossRefGoogle Scholar
Lebowitz, J. and Maes, C. (1987). The effect of an external field on an interface, entropic repulsion. J. Statist. Phys. 46, 39–49.CrossRefGoogle Scholar
Roy, R. (2016). Extreme values of log-correlated Gaussian fields. Doctoral thesis, University of Chicago.Google Scholar
Schweiger, F. (2020). The maximum of the four-dimensional membrane model. Ann. Prob. 48, 714–741.CrossRefGoogle Scholar
Slepian, D. (1962). The one-sided barrier problem for Gaussian noise. Bell System Tech. J. 41, 463–501.CrossRefGoogle Scholar
Zeitouni, O. Branching random walks and Gaussian fields. Lecture notes.Google Scholar