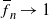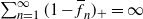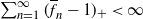1. Introduction
A Galton–Watson branching process in varying environment (BPVE)
![]() $(X_n, \, n \geq 0)$
is defined as
$(X_n, \, n \geq 0)$
is defined as
 \begin{equation} X_0 = 1, \qquad X_n = \sum_{j=1}^{X_{n-1}} \xi_{n,j}, \quad n\in\mathbb{N} = \{ 1, 2, \ldots \},\end{equation}
\begin{equation} X_0 = 1, \qquad X_n = \sum_{j=1}^{X_{n-1}} \xi_{n,j}, \quad n\in\mathbb{N} = \{ 1, 2, \ldots \},\end{equation}
where
![]() $\{\xi_{n,j}\}_{n, j \in \mathbb{N}}$
are nonnegative independent random variables such that, for each n,
$\{\xi_{n,j}\}_{n, j \in \mathbb{N}}$
are nonnegative independent random variables such that, for each n,
![]() $\{\xi_{n,j}\}_{j \in \mathbb{N}}$
are identically distributed; let
$\{\xi_{n,j}\}_{j \in \mathbb{N}}$
are identically distributed; let
![]() $\xi_n$
denote a generic copy. We can interpret
$\xi_n$
denote a generic copy. We can interpret
![]() $X_n$
as the size of the nth generation of a population, and
$X_n$
as the size of the nth generation of a population, and
![]() $\xi_{n,j}$
represents the number of offspring produced by the jth individual in generation
$\xi_{n,j}$
represents the number of offspring produced by the jth individual in generation
![]() $n-1$
. These processes are natural extensions of usual homogeneous Galton–Watson processes, where the offspring distribution does not change with the generation.
$n-1$
. These processes are natural extensions of usual homogeneous Galton–Watson processes, where the offspring distribution does not change with the generation.
The investigation of BPVE started in the early 1970s [Reference Church4, Reference Fearn6]. There has been recent increasing interest in these processes, which was triggered by Kersting [Reference Kersting15], who obtained a necessary and sufficient condition for almost-sure extinction for regular processes. In [Reference Kersting15] he introduced the shape function of a generating function (g.f.), which turned out to be the appropriate tool for the analysis. Moreover, in [Reference Kersting15] Yaglom-type limit theorems (i.e. conditioned on nonextinction) were obtained. In [Reference Bhattacharya and Perlman2], under different regularity conditions, Yaglom-type limit theorems were proved in both discrete- and continuous-time settings, extending the results of [Reference Jagers14]. For multitype processes these questions were investigated in [Reference Dolgopyat, Hebbar, Koralov and Perlman5]. In [Reference Cardona-Tobón and Palau3], the authors obtained probabilistic proofs of the results in [Reference Kersting15] using spine decomposition. On the general theory of BPVE we refer to the recent monograph [Reference Kersting and Vatutin16], and to the references therein.
Here we are interested in branching processes in nearly degenerate varying environment. Let
![]() $f_n(s) = \mathbb{E} s^{\xi_n}$
,
$f_n(s) = \mathbb{E} s^{\xi_n}$
,
![]() $s \in [0,1]$
, denote the g.f. of the offspring distribution of the nth generation, and put
$s \in [0,1]$
, denote the g.f. of the offspring distribution of the nth generation, and put
![]() $\overline{f}_n \;:\!=\; f_n^{\prime}(1) = \mathbb{E} \xi_n$
for the offspring mean. We assume the following conditions:
$\overline{f}_n \;:\!=\; f_n^{\prime}(1) = \mathbb{E} \xi_n$
for the offspring mean. We assume the following conditions:
-
(C1)
 $\lim_{n\to\infty}\overline{f}_n = 1$
,
$\lim_{n\to\infty}\overline{f}_n = 1$
,
 $\sum_{n=1}^{\infty}(1-\overline{f}_n)_+ = \infty$
,
$\sum_{n=1}^{\infty}(1-\overline{f}_n)_+ = \infty$
,
 $\sum_{n=1}^\infty (\overline{f}_n - 1)_+ < \infty$
.
$\sum_{n=1}^\infty (\overline{f}_n - 1)_+ < \infty$
. -
(C2)
 $\lim_{n\to\infty, \overline{f}_n < 1} \dfrac{f_n^{\prime\prime}(1)}{1-\overline{f}_n} = \nu \in [0,\infty)$
, and
$\lim_{n\to\infty, \overline{f}_n < 1} \dfrac{f_n^{\prime\prime}(1)}{1-\overline{f}_n} = \nu \in [0,\infty)$
, and
 $\dfrac{f_n^{\prime\prime}(1)}{|1- \overline{f}_n|}$
is bounded.
$\dfrac{f_n^{\prime\prime}(1)}{|1- \overline{f}_n|}$
is bounded. -
(C3) If
 $\nu>0$
, then
$\nu>0$
, then
 $\lim_{n\to \infty, \overline{f}_n < 1}\dfrac{f_n^{\prime\prime\prime}(1)}{1- \overline{f}_n} = 0$
, and
$\lim_{n\to \infty, \overline{f}_n < 1}\dfrac{f_n^{\prime\prime\prime}(1)}{1- \overline{f}_n} = 0$
, and
 $\dfrac{f_n^{\prime\prime\prime}(1)}{|1- \overline{f}_n|}$
is bounded.
$\dfrac{f_n^{\prime\prime\prime}(1)}{|1- \overline{f}_n|}$
is bounded.
Here and later on,
![]() $\lim_{n \to \infty, \overline{f}_n < 1}$
means that the convergence holds along the subsequence
$\lim_{n \to \infty, \overline{f}_n < 1}$
means that the convergence holds along the subsequence
![]() $\{n \colon \overline{f}_n < 1\}$
, and
$\{n \colon \overline{f}_n < 1\}$
, and
![]() $a_+ = \max \{ a, 0\}$
. Condition (C1) means that the process is nearly critical and the convergence
$a_+ = \max \{ a, 0\}$
. Condition (C1) means that the process is nearly critical and the convergence
![]() $\overline{f}_n \to 1$
is not too fast. Note that we also allow supercritical generations, i.e. with
$\overline{f}_n \to 1$
is not too fast. Note that we also allow supercritical generations, i.e. with
![]() $\overline{f}_n > 1$
. However, subcritical regimes dominate since, by (C1),
$\overline{f}_n > 1$
. However, subcritical regimes dominate since, by (C1),
![]() $\mathbb{E} X_n = \prod_{j=1}^n \overline{f}_j \to 0$
, and thus the process dies out almost surely.
$\mathbb{E} X_n = \prod_{j=1}^n \overline{f}_j \to 0$
, and thus the process dies out almost surely.
Condition (C2) implies that
![]() $f_n^{\prime\prime}(1) \to 0$
, thus
$f_n^{\prime\prime}(1) \to 0$
, thus
![]() $f_n(s) \to s$
, so the branching mechanism converges to degenerate branching. Therefore, this nearly critical model does not have a natural homogeneous counterpart. To obtain nontrivial limit theorems we can condition on nonextinction, or add immigration. Note that condition (C2) implies that the offspring distributions have finite second moment, which is assumed throughout the paper.
$f_n(s) \to s$
, so the branching mechanism converges to degenerate branching. Therefore, this nearly critical model does not have a natural homogeneous counterpart. To obtain nontrivial limit theorems we can condition on nonextinction, or add immigration. Note that condition (C2) implies that the offspring distributions have finite second moment, which is assumed throughout the paper.
Conditioned on
![]() $X_n > 0$
, in our Theorem 1 we prove that
$X_n > 0$
, in our Theorem 1 we prove that
![]() $X_n$
converges in distribution without normalization to a geometric distribution. Although the process is nearly critical, in this sense its behavior is similar to a homogeneous subcritical process, where no normalization is needed to obtain a limit; see Yaglom’s theorem [Reference Yaglom21] (or [Reference Athreya and Ney1, Theorem I.8.1, Corollary I.8.1]). For a regular BPVE (in the sense of [Reference Kersting15]), necessary and sufficient conditions were obtained for the tightness of
$X_n$
converges in distribution without normalization to a geometric distribution. Although the process is nearly critical, in this sense its behavior is similar to a homogeneous subcritical process, where no normalization is needed to obtain a limit; see Yaglom’s theorem [Reference Yaglom21] (or [Reference Athreya and Ney1, Theorem I.8.1, Corollary I.8.1]). For a regular BPVE (in the sense of [Reference Kersting15]), necessary and sufficient conditions were obtained for the tightness of
![]() $X_n$
(without normalization) conditioned on
$X_n$
(without normalization) conditioned on
![]() $X_n > 0$
in [Reference Kersting15, Corollary 2]. However, to the best of our knowledge, our result is the first proper limit theorem without normalization. Similarly to Yaglom’s theorem in the homogeneous critical case (see [Reference Yaglom21] or [Reference Athreya and Ney1, Theorem I.9.2]), exponential limits for properly normalized processes conditioned on non-extinction were obtained in several papers; see, e.g., [Reference Bhattacharya and Perlman2, Reference Jagers14, Reference Kersting15].
$X_n > 0$
in [Reference Kersting15, Corollary 2]. However, to the best of our knowledge, our result is the first proper limit theorem without normalization. Similarly to Yaglom’s theorem in the homogeneous critical case (see [Reference Yaglom21] or [Reference Athreya and Ney1, Theorem I.9.2]), exponential limits for properly normalized processes conditioned on non-extinction were obtained in several papers; see, e.g., [Reference Bhattacharya and Perlman2, Reference Jagers14, Reference Kersting15].
Allowing immigration usually leads to similar behavior to conditioning on nonextinction. A branching process in varying environment with immigration
![]() $(Y_n, \, n \geq 0)$
is defined as
$(Y_n, \, n \geq 0)$
is defined as
 \begin{equation} Y_0=0, \qquad Y_n=\sum_{j=1}^{Y_{n-1}}\xi_{n,j}+\varepsilon_n, \quad n\in\mathbb{N},\end{equation}
\begin{equation} Y_0=0, \qquad Y_n=\sum_{j=1}^{Y_{n-1}}\xi_{n,j}+\varepsilon_n, \quad n\in\mathbb{N},\end{equation}
where
![]() $\{\xi_n, \xi_{n,j}, \varepsilon_n\}_{n, j \in \mathbb{N}}$
are nonnegative, independent random variables such that
$\{\xi_n, \xi_{n,j}, \varepsilon_n\}_{n, j \in \mathbb{N}}$
are nonnegative, independent random variables such that
![]() $\{\xi_n, \xi_{n,j}\}_{j \in \mathbb{N}}$
are identically distributed. As before,
$\{\xi_n, \xi_{n,j}\}_{j \in \mathbb{N}}$
are identically distributed. As before,
![]() $\xi_{n,j}$
is the number of offspring of the jth individual in generation
$\xi_{n,j}$
is the number of offspring of the jth individual in generation
![]() $n-1$
, and
$n-1$
, and
![]() $\varepsilon_n$
is the number of immigrants.
$\varepsilon_n$
is the number of immigrants.
The study of nearly degenerate BPVE with immigration was initiated in [Reference Györfi, Ispány, Pap and Varga12], where it was assumed that the offspring have Bernoulli distribution. The most interesting finding in [Reference Györfi, Ispány, Pap and Varga12] is that the slow dying out effect can be balanced by a slow immigration rate to obtain a nontrivial distributional limit without normalization. In this case the resulting process is an inhomogeneous first-order integer-valued autoregressive process (INAR(1)). INAR processes are important in various fields of applied probability; for the theory and applications we refer to the survey in [Reference Weiß20]. The setup of [Reference Györfi, Ispány, Pap and Varga12] was extended by [Reference Kevei17], allowing more general offspring distributions. For INAR(1) processes the condition
![]() $\overline{f}_n < 1$
is automatic (being a probability), while in the more general setup of [Reference Kevei17] it was assumed. Our conditions (C1) and (C2) do allow supercritical generations, i.e.
$\overline{f}_n < 1$
is automatic (being a probability), while in the more general setup of [Reference Kevei17] it was assumed. Our conditions (C1) and (C2) do allow supercritical generations, i.e.
![]() $\overline{f}_n > 1$
, with a dominating subcritical regime. The multitype case was studied in [Reference Györfi, Ispány, Kevei and Pap11].
$\overline{f}_n > 1$
, with a dominating subcritical regime. The multitype case was studied in [Reference Györfi, Ispány, Kevei and Pap11].
In general, Galton–Watson processes with immigration in varying environment (i.e. with time-dependent immigration) are less studied. In [Reference Gao and Zhang8], the central limit theorem and law of the iterated logarithm were proved. In [Reference Ispány13], a diffusion approximation was obtained in the strongly critical case, i.e. when, instead of (C1), the condition
![]() $\sum_{n=1}^\infty |1 - \overline{f}_n| < \infty$
holds. [Reference González, Kersting, Minuesa and del Puerto9] investigated almost-sure extinction, and obtained limit theorems for the properly normalized process. Since we prove limit theorems for the process without normalization, both our results and assumptions are rather different from those in the papers mentioned.
$\sum_{n=1}^\infty |1 - \overline{f}_n| < \infty$
holds. [Reference González, Kersting, Minuesa and del Puerto9] investigated almost-sure extinction, and obtained limit theorems for the properly normalized process. Since we prove limit theorems for the process without normalization, both our results and assumptions are rather different from those in the papers mentioned.
Generalizing the results in [Reference Kevei17], in Theorems 2 and 3 we show that, under appropriate assumptions on the immigration, the slow extinction trend and the slow immigration trend are balanced and we get a nontrivial compound-Poisson limit distribution without normalization.
The rest of the paper is organized as follows. Section 2 contains the main results. All the proofs are gathered together in Section 3. The proofs are rather technical, and based on analysis of the composite g.f. We rely on the shape function technique worked out in [Reference Kersting15].
2. Main results
2.1. Yaglom-type limit theorems
Consider the BPVE
![]() $(X_n)$
in (1). Condition (C1) implies that the process dies out almost surely. In [Reference Kersting15] a BPVE process
$(X_n)$
in (1). Condition (C1) implies that the process dies out almost surely. In [Reference Kersting15] a BPVE process
![]() $(X_n)$
is called regular if
$(X_n)$
is called regular if
holds for some
![]() $c > 0$
and for all n, where
$c > 0$
and for all n, where
![]() $\mathbf{1}$
stands for the indicator function. In our setup, if (C1)–(C3) are satisfied with
$\mathbf{1}$
stands for the indicator function. In our setup, if (C1)–(C3) are satisfied with
![]() $\nu > 0$
then the process is regular, while if
$\nu > 0$
then the process is regular, while if
![]() $\nu = 0$
there are nonregular examples (e.g.
$\nu = 0$
there are nonregular examples (e.g.
![]() $\mathbb{P} ( \xi_n = 0) = n^{-1}$
,
$\mathbb{P} ( \xi_n = 0) = n^{-1}$
,
![]() $\mathbb{P} (\xi_n = 1) = 1 - n^{-1} - n^{-4}$
,
$\mathbb{P} (\xi_n = 1) = 1 - n^{-1} - n^{-4}$
,
![]() $\mathbb{P}( \xi_n = n) = n^{-4}$
works). For regular processes the results in [Reference Kersting15] apply. According to Kersting’s classification of regular BPVEs [Reference Kersting15, Proposition 1], a regular process satisfying (C1)–(C3) is subcritical. Indeed,
$\mathbb{P}( \xi_n = n) = n^{-4}$
works). For regular processes the results in [Reference Kersting15] apply. According to Kersting’s classification of regular BPVEs [Reference Kersting15, Proposition 1], a regular process satisfying (C1)–(C3) is subcritical. Indeed,
![]() $\mathbb{E} X_n \to 0$
and, by Lemma 2 and (C2),
$\mathbb{E} X_n \to 0$
and, by Lemma 2 and (C2),
 \[ \lim_{n \to \infty}\overline{f}_{0,n} \sum_{k=1}^n \frac{f^{\prime\prime}_k(1)}{\overline{f}_{0,k-1} \overline{f}_k^2} = \nu.\]
\[ \lim_{n \to \infty}\overline{f}_{0,n} \sum_{k=1}^n \frac{f^{\prime\prime}_k(1)}{\overline{f}_{0,k-1} \overline{f}_k^2} = \nu.\]
Furthermore, [Reference Kersting15, Corollary 2] states that the sequence
![]() $\mathcal{L}(X_n \mid X_n > 0)$
is tight if and only if
$\mathcal{L}(X_n \mid X_n > 0)$
is tight if and only if
![]() $\sup_{n \geq 0} \mathbb{E} [ X_n \mid X_n > 0] < \infty$
. Here,
$\sup_{n \geq 0} \mathbb{E} [ X_n \mid X_n > 0] < \infty$
. Here,
![]() $\mathcal{L}(X_n\mid X_n>0)$
stands for the law of
$\mathcal{L}(X_n\mid X_n>0)$
stands for the law of
![]() $X_n$
conditioned on nonextinction. In Lemma 4 we show that the latter condition holds; in fact the limit exists. Therefore, the sequence of conditional laws is tight. In the next result, we prove that the limit distribution also exists.
$X_n$
conditioned on nonextinction. In Lemma 4 we show that the latter condition holds; in fact the limit exists. Therefore, the sequence of conditional laws is tight. In the next result, we prove that the limit distribution also exists.
The random variable V has geometric distribution with parameter
![]() $p \in (0,1]$
,
$p \in (0,1]$
,
![]() $V \sim \textrm{Geom}(p)$
, if
$V \sim \textrm{Geom}(p)$
, if
![]() $\mathbb{P}(V = k) = (1-p)^{k-1} p$
,
$\mathbb{P}(V = k) = (1-p)^{k-1} p$
,
![]() $k=1,2,\ldots$
$k=1,2,\ldots$
Theorem 1. Assume that (C1)–(C3) are satisfied. Then, for the BPVE
![]() $(X_n)$
in (1),
$(X_n)$
in (1),
as
![]() $n\to\infty$
, where
$n\to\infty$
, where
![]() $\overset{\textrm{D}}{\longrightarrow}$
denotes convergence in distribution.
$\overset{\textrm{D}}{\longrightarrow}$
denotes convergence in distribution.
The result holds with
![]() $\nu = 0$
, in which case the sequence of random variables converges in probability to 1.
$\nu = 0$
, in which case the sequence of random variables converges in probability to 1.
Example 1. Let
![]() $f_n(s) = f_n[0] + f_n[1] s + f_n[2] s^2$
; then
$f_n(s) = f_n[0] + f_n[1] s + f_n[2] s^2$
; then
![]() $\overline{f}_n = f_n[1] + 2 f_n[2]$
,
$\overline{f}_n = f_n[1] + 2 f_n[2]$
,
![]() $f_n^{\prime\prime}(1) = 2 f_n[2]$
, and
$f_n^{\prime\prime}(1) = 2 f_n[2]$
, and
![]() $f_n^{\prime\prime\prime}(1) = 0$
. Assuming that
$f_n^{\prime\prime\prime}(1) = 0$
. Assuming that
![]() $f_n[0]+f_n[2] \to 0$
,
$f_n[0]+f_n[2] \to 0$
,
![]() $f_n[0]> f_n[2]$
,
$f_n[0]> f_n[2]$
,
![]() $\sum_{n=1}^\infty (f_n[0] - f_n[2]) = \infty$
, and
$\sum_{n=1}^\infty (f_n[0] - f_n[2]) = \infty$
, and
![]() $2 f_n[2] / ( f_n[0]- f_n[2]) \to \nu \in [0,\infty)$
as
$2 f_n[2] / ( f_n[0]- f_n[2]) \to \nu \in [0,\infty)$
as
![]() $n\to\infty$
, the conditions of Theorem 1 are fulfilled.
$n\to\infty$
, the conditions of Theorem 1 are fulfilled.
2.2. Nearly degenerate branching processes with immigration
Recall
![]() $(Y_n)$
, the BPVE with immigration from (2), and introduce the factorial moments of the immigration
$(Y_n)$
, the BPVE with immigration from (2), and introduce the factorial moments of the immigration
![]() $m_{n,k} \;:\!=\; \mathbb{E} [\varepsilon_n(\varepsilon_n-1) \cdots (\varepsilon_n-k+1)]$
,
$m_{n,k} \;:\!=\; \mathbb{E} [\varepsilon_n(\varepsilon_n-1) \cdots (\varepsilon_n-k+1)]$
,
![]() $k\in \mathbb{N}$
.
$k\in \mathbb{N}$
.
Theorem 2. Assume that (C1)–(C3) are satisfied, and also
-
(C4)
 $\lim_{n\to\infty, \overline{f}_n < 1}{m_{n,k}}/{(k!(1-\overline{f}_n))} = \lambda_k$
,
$\lim_{n\to\infty, \overline{f}_n < 1}{m_{n,k}}/{(k!(1-\overline{f}_n))} = \lambda_k$
,
 $k = 1,2,\ldots,K$
, with
$k = 1,2,\ldots,K$
, with
 $\lambda_K=0$
, and for each
$\lambda_K=0$
, and for each
 $k \leq K$
the sequence
$k \leq K$
the sequence
 $(m_{n,k}/|1-\overline{f}_n|)_n$
is bounded.
$(m_{n,k}/|1-\overline{f}_n|)_n$
is bounded.
Then, for the BPVE with immigration
![]() $(Y_n)$
in (2),
$(Y_n)$
in (2),
![]() $Y_n\overset{\textrm{D}}{\longrightarrow} Y$
as
$Y_n\overset{\textrm{D}}{\longrightarrow} Y$
as
![]() $n\to\infty$
, where the random variable Y has compound-Poisson distribution and, for its g.f.
$n\to\infty$
, where the random variable Y has compound-Poisson distribution and, for its g.f.
![]() $f_Y$
,
$f_Y$
,
 \[ \log f_Y(s) = \begin{cases} -\sum\limits_{k=1}^{K-1}\dfrac{2^k\lambda_k}{\nu^k}\Bigg(\log\bigg(1+\dfrac{\nu}{2}(1-s)\bigg) + \sum\limits_{i=1}^{k-1}\dfrac{\nu^i}{i2^i}(s-1)^i\Bigg), & \nu > 0, \\[4mm] \sum\limits_{k=1}^{K-1}\dfrac{\lambda_k}{k}(s-1)^k, & \nu = 0. \end{cases} \]
\[ \log f_Y(s) = \begin{cases} -\sum\limits_{k=1}^{K-1}\dfrac{2^k\lambda_k}{\nu^k}\Bigg(\log\bigg(1+\dfrac{\nu}{2}(1-s)\bigg) + \sum\limits_{i=1}^{k-1}\dfrac{\nu^i}{i2^i}(s-1)^i\Bigg), & \nu > 0, \\[4mm] \sum\limits_{k=1}^{K-1}\dfrac{\lambda_k}{k}(s-1)^k, & \nu = 0. \end{cases} \]
Note that
![]() $f_Y$
is continuous in
$f_Y$
is continuous in
![]() $\nu \in [0,\infty)$
. Under further assumptions we might allow infinitely many nonzero
$\nu \in [0,\infty)$
. Under further assumptions we might allow infinitely many nonzero
![]() $\lambda$
s.
$\lambda$
s.
Theorem 3. Assume that (C1)–(C3) are satisfied, and
-
(C4ʹ)
 $\lim_{n\to\infty, \overline{f}_n < 1}{m_{n,k}}/{(k!(1-\overline{f}_n))} = \lambda_k$
,
$\lim_{n\to\infty, \overline{f}_n < 1}{m_{n,k}}/{(k!(1-\overline{f}_n))} = \lambda_k$
,
 $k=1,2,\ldots$
, such that
$k=1,2,\ldots$
, such that
 $\limsup_{n \to \infty} \lambda_n^{1/n} \leq 1$
, and
$\limsup_{n \to \infty} \lambda_n^{1/n} \leq 1$
, and
 $(m_{n,k}/|1-\overline{f}_n|)_n$
is bounded for each k.
$(m_{n,k}/|1-\overline{f}_n|)_n$
is bounded for each k.
Then, for the BPVE with immigration
![]() $(Y_n)$
in (2),
$(Y_n)$
in (2),
![]() $Y_n \overset{\textrm{D}}{\longrightarrow} Y$
as
$Y_n \overset{\textrm{D}}{\longrightarrow} Y$
as
![]() $n\to\infty$
, where the random variable Y has compound-Poisson distribution and, for its g.f.
$n\to\infty$
, where the random variable Y has compound-Poisson distribution and, for its g.f.
![]() $f_Y$
,
$f_Y$
,
 \begin{equation} \log f_Y(s) = \begin{cases} -\sum\limits_{k=1}^{\infty}\dfrac{2^k\lambda_k}{\nu^k}\Bigg(\log\bigg(1+\dfrac{\nu}{2}(1-s)\bigg) + \sum\limits_{i=1}^{k-1}\dfrac{\nu^i}{i2^i}(s-1)^i\Bigg), & \nu > 0, \\[4mm] \sum\limits_{k=1}^{\infty}\dfrac{\lambda_k}{k} (s-1)^k, & \nu = 0. \end{cases} \end{equation}
\begin{equation} \log f_Y(s) = \begin{cases} -\sum\limits_{k=1}^{\infty}\dfrac{2^k\lambda_k}{\nu^k}\Bigg(\log\bigg(1+\dfrac{\nu}{2}(1-s)\bigg) + \sum\limits_{i=1}^{k-1}\dfrac{\nu^i}{i2^i}(s-1)^i\Bigg), & \nu > 0, \\[4mm] \sum\limits_{k=1}^{\infty}\dfrac{\lambda_k}{k} (s-1)^k, & \nu = 0. \end{cases} \end{equation}
Remark 1. If
![]() $K=2$
in Theorem 2 then Y has (generalized) negative binomial distribution with parameters
$K=2$
in Theorem 2 then Y has (generalized) negative binomial distribution with parameters
![]() ${2\lambda_1}/{\nu}$
(not necessarily integer) and
${2\lambda_1}/{\nu}$
(not necessarily integer) and
![]() ${2}/({2+\nu})$
as shown in [Reference Kevei17, Theorem 5]. In particular, Theorems 2 and 3 are generalizations of [Reference Kevei17, Theorem 5].
${2}/({2+\nu})$
as shown in [Reference Kevei17, Theorem 5]. In particular, Theorems 2 and 3 are generalizations of [Reference Kevei17, Theorem 5].
If
![]() $\nu = 0$
in condition (C2), then the results in Theorems 2 and 3 follow from [Reference Kevei17, Theorem 4] when
$\nu = 0$
in condition (C2), then the results in Theorems 2 and 3 follow from [Reference Kevei17, Theorem 4] when
![]() $\overline{f}_n < 1$
for all n. Our results are new even in this special case.
$\overline{f}_n < 1$
for all n. Our results are new even in this special case.
Remark 2. Conditions (C4) and (C4ʹ) mean that the immigration is of the proper order, i.e.
![]() $\lim_{n \to \infty, \overline{f}_n < 1}{\mathbb{P}(\varepsilon_n = j)}/({1 - \overline{f}_n})$
exists for each
$\lim_{n \to \infty, \overline{f}_n < 1}{\mathbb{P}(\varepsilon_n = j)}/({1 - \overline{f}_n})$
exists for each
![]() $j \geq 1$
; see Theorem 4.
$j \geq 1$
; see Theorem 4.
Conditions (C4) and (C4ʹ) are not comparable in the sense that neither implies the other. Indeed, if (C4) holds with
![]() $K = 3$
, then it is possible that fourth moments do not exist, while in (C4ʹ) all moments have to be finite.
$K = 3$
, then it is possible that fourth moments do not exist, while in (C4ʹ) all moments have to be finite.
We can construct examples for which
![]() $\lambda_2 = 0$
,
$\lambda_2 = 0$
,
![]() $\lambda_3=1$
,
$\lambda_3=1$
,
![]() $\lambda_4 = \infty$
. In this case (C4) in Theorem 2 holds with
$\lambda_4 = \infty$
. In this case (C4) in Theorem 2 holds with
![]() $K= 2$
. On the other hand, it is easy to show that if
$K= 2$
. On the other hand, it is easy to show that if
![]() $\lambda_{n_1} = \lambda_{n_2} = 0$
for some
$\lambda_{n_1} = \lambda_{n_2} = 0$
for some
![]() $n_1 < n_2$
, then
$n_1 < n_2$
, then
![]() $\lambda_n = 0$
for
$\lambda_n = 0$
for
![]() $n_1 < n < n_2$
.
$n_1 < n < n_2$
.
The g.f.
![]() $f_Y$
of the limit has a rather complicated form. In the proof, showing the pointwise convergence of the generating functions, we prove that the accompanying laws converge in distribution to Y. Since the accompanying laws are compound-Poisson, this implies (see, e.g., [Reference Steutel and van Harn19, Proposition 2.2]) that the limit Y is compound-Poisson too. That is,
$f_Y$
of the limit has a rather complicated form. In the proof, showing the pointwise convergence of the generating functions, we prove that the accompanying laws converge in distribution to Y. Since the accompanying laws are compound-Poisson, this implies (see, e.g., [Reference Steutel and van Harn19, Proposition 2.2]) that the limit Y is compound-Poisson too. That is,
![]() $Y = \sum_{i=1}^N Z_i$
, where
$Y = \sum_{i=1}^N Z_i$
, where
![]() $Z, Z_1, Z_2, \ldots$
are independent and identically distributed nonnegative integer-valued random variables, and independently N has Poisson distribution. This is an important class of distributions, since it is exactly the class of infinitely divisible distributions on the nonnegative integers; see, e.g., [Reference Steutel and van Harn19, Theorem II.3.2]. Interestingly, from the form of the g.f.
$Z, Z_1, Z_2, \ldots$
are independent and identically distributed nonnegative integer-valued random variables, and independently N has Poisson distribution. This is an important class of distributions, since it is exactly the class of infinitely divisible distributions on the nonnegative integers; see, e.g., [Reference Steutel and van Harn19, Theorem II.3.2]. Interestingly, from the form of the g.f.
![]() $f_Y$
it is difficult to deduce that it is compound-Poisson, because the logarithm is given as a power series in
$f_Y$
it is difficult to deduce that it is compound-Poisson, because the logarithm is given as a power series in
![]() $1-s$
, while for the compound-Poisson this is a power series in s. Under some conditions on the sequence
$1-s$
, while for the compound-Poisson this is a power series in s. Under some conditions on the sequence
![]() $(\lambda_n)$
we can rewrite
$(\lambda_n)$
we can rewrite
![]() $\log f_Y$
to a series expansion in s, which allows us to understand the structure of the limit.
$\log f_Y$
to a series expansion in s, which allows us to understand the structure of the limit.
Theorem 4. Assume one of the following:
-
(i) the conditions of Theorem 2 hold; or
-
(ii) the conditions of Theorem 3 hold and
 $\limsup_{n\to \infty}\lambda_n^{1/n} \leq \frac12$
.
$\limsup_{n\to \infty}\lambda_n^{1/n} \leq \frac12$
.
Then the limiting g.f. in Theorems 2 and 3 can be written as
 \[ f_Y(s) = \exp\Bigg\{\sum_{n=1}^\infty A_n(s^n - 1)\Bigg\}, \]
\[ f_Y(s) = \exp\Bigg\{\sum_{n=1}^\infty A_n(s^n - 1)\Bigg\}, \]
where
 \begin{align*} A_n & = \begin{cases} \dfrac{\nu^n}{n (2+\nu)^n}\sum\limits_{j=1}^\infty q_j\bigg[\bigg(1 + \dfrac{2}{\nu}\bigg)^{\min(j,n)} - 1\bigg], & \nu > 0, \\[4mm] \dfrac{1}{n}\sum\limits_{j=n}^\infty q_j, & \nu = 0, \end{cases} \\ q_j & = \lim_{n\to\infty, \overline{f}_n < 1}\frac{\mathbb{P}(\varepsilon_n = j)}{1 - \overline{f}_n}, \quad j=1,2,\ldots \end{align*}
\begin{align*} A_n & = \begin{cases} \dfrac{\nu^n}{n (2+\nu)^n}\sum\limits_{j=1}^\infty q_j\bigg[\bigg(1 + \dfrac{2}{\nu}\bigg)^{\min(j,n)} - 1\bigg], & \nu > 0, \\[4mm] \dfrac{1}{n}\sum\limits_{j=n}^\infty q_j, & \nu = 0, \end{cases} \\ q_j & = \lim_{n\to\infty, \overline{f}_n < 1}\frac{\mathbb{P}(\varepsilon_n = j)}{1 - \overline{f}_n}, \quad j=1,2,\ldots \end{align*}
Remark 3. For
![]() $\nu = 0$
, the latter formula was obtained in [Reference Györfi, Ispány, Pap and Varga12, Remark 2]. In fact, the last limit exists without any extra conditions on the
$\nu = 0$
, the latter formula was obtained in [Reference Györfi, Ispány, Pap and Varga12, Remark 2]. In fact, the last limit exists without any extra conditions on the
![]() $(\lambda_n)_n$
sequence, see Lemma 8. Furthermore, it is clear that under (C4),
$(\lambda_n)_n$
sequence, see Lemma 8. Furthermore, it is clear that under (C4),
![]() $q_k = 0$
for
$q_k = 0$
for
![]() $k \geq K$
. The form of
$k \geq K$
. The form of
![]() $f_Y$
also implies that the limit has the representation
$f_Y$
also implies that the limit has the representation
![]() $Y = \sum_{n=1}^\infty n N_n$
, where
$Y = \sum_{n=1}^\infty n N_n$
, where
![]() $(N_n)$
are independent Poisson random variables, such that
$(N_n)$
are independent Poisson random variables, such that
![]() $N_n$
has parameter
$N_n$
has parameter
![]() $A_n$
.
$A_n$
.
3. Proofs
3.1. Preparation
In the proofs, we analyze the g.f. of the underlying processes. To prove distributional convergence for nonnegative integer-valued processes, it is enough to prove the pointwise convergence of the g.f., and show that the limit is a g.f. as well [Reference Feller7, p. 280].
Recall that
![]() $f_n(s) = \mathbb{E} s^{\xi_n}$
represents the offspring g.f. in generation n. For the composite g.f., introduce the notation
$f_n(s) = \mathbb{E} s^{\xi_n}$
represents the offspring g.f. in generation n. For the composite g.f., introduce the notation
![]() $f_{n,n}(s) = s$
and, for
$f_{n,n}(s) = s$
and, for
![]() $j < n$
,
$j < n$
,
![]() $f_{j,n}(s) \;:\!=\; f_{j+1} \circ \cdots \circ f_n(s)$
; and for the corresponding means
$f_{j,n}(s) \;:\!=\; f_{j+1} \circ \cdots \circ f_n(s)$
; and for the corresponding means
![]() $\overline{f}_{n,n} = 1$
and
$\overline{f}_{n,n} = 1$
and
![]() $\overline{f}_{j,n} \;:\!=\; \overline{f}_{j+1} \cdots \overline{f}_n$
,
$\overline{f}_{j,n} \;:\!=\; \overline{f}_{j+1} \cdots \overline{f}_n$
,
![]() $j <n$
. Then it is well known that
$j <n$
. Then it is well known that
![]() $\mathbb{E} s^{X_n} = f_{0,n}(s)$
and
$\mathbb{E} s^{X_n} = f_{0,n}(s)$
and
![]() $\mathbb{E} X_n = \overline{f}_{0,n}$
.
$\mathbb{E} X_n = \overline{f}_{0,n}$
.
For a g.f. f, with mean
![]() $\overline{f}$
and
$\overline{f}$
and
![]() $f^{\prime\prime}(1) < \infty$
, define the shape function as
$f^{\prime\prime}(1) < \infty$
, define the shape function as
Let
![]() $\varphi_j$
be the shape function of
$\varphi_j$
be the shape function of
![]() $f_j$
. By the definition of
$f_j$
. By the definition of
![]() $f_{j,n}$
,
$f_{j,n}$
,
Therefore, iteration gives ([Reference Kersting15, Lemma 5], [Reference Kersting and Vatutin16, Proposition 1.3])
where
 \begin{equation} \varphi_{j,n}(s)\;:\!=\;\sum_{k=j+1}^{n} \frac{\varphi_k(f_{k,n}(s))}{\overline{f}_{j,k-1}}.\end{equation}
\begin{equation} \varphi_{j,n}(s)\;:\!=\;\sum_{k=j+1}^{n} \frac{\varphi_k(f_{k,n}(s))}{\overline{f}_{j,k-1}}.\end{equation}
The latter formulas show the usefulness of the shape function. The next statement gives precise upper and lower bounds on the shape function.
Lemma 1. ([Reference Kersting15, Lemma 1], [Reference Kersting and Vatutin16, Proposition 1.4].) Assume
![]() $0<\overline{f}<\infty$
,
$0<\overline{f}<\infty$
,
![]() $f^{\prime\prime}(1)<\infty$
, and let
$f^{\prime\prime}(1)<\infty$
, and let
![]() $\varphi(s)$
be the shape function of f. Then, for
$\varphi(s)$
be the shape function of f. Then, for
![]() $0\leq s\leq 1$
,
$0\leq s\leq 1$
,
![]() $\frac{1}{2}\varphi(0)\leq \varphi(s)\leq 2\varphi(1)$
.
$\frac{1}{2}\varphi(0)\leq \varphi(s)\leq 2\varphi(1)$
.
For further properties of shape functions we refer to [Reference Kersting and Vatutin16, Chapter 1] and [Reference Kersting15].
We frequently use the following extension of [Reference Györfi, Ispány, Pap and Varga12, Lemma 5], which is a version of the Silverman–Toeplitz theorem.
Lemma 2. Let
![]() $(\overline{f}_n)_{n\in\mathbb{N}}$
be a sequence of positive real numbers satisfying (C1), and define
$(\overline{f}_n)_{n\in\mathbb{N}}$
be a sequence of positive real numbers satisfying (C1), and define
 \begin{align*} a_{n,j}^{(k)} & = (1-\overline{f}_j)\prod_{i=j+1}^{n}\overline{f}_i^k = (1 - \overline{f}_j) \overline{f}_{j,n}^k, \qquad n,j,k\in\mathbb{N}, \ j\leq n-1, \\ a_{n,n}^{(k)} & = 1 - \overline{f}_n. \end{align*}
\begin{align*} a_{n,j}^{(k)} & = (1-\overline{f}_j)\prod_{i=j+1}^{n}\overline{f}_i^k = (1 - \overline{f}_j) \overline{f}_{j,n}^k, \qquad n,j,k\in\mathbb{N}, \ j\leq n-1, \\ a_{n,n}^{(k)} & = 1 - \overline{f}_n. \end{align*}
If
![]() $(x_n)_{n\in\mathbb{N}}$
is bounded and
$(x_n)_{n\in\mathbb{N}}$
is bounded and
![]() $\lim_{n\to\infty,\overline{f}_n < 1}x_n = x \in \mathbb{R}$
, then, for all
$\lim_{n\to\infty,\overline{f}_n < 1}x_n = x \in \mathbb{R}$
, then, for all
![]() $k\in\mathbb{N}$
,
$k\in\mathbb{N}$
,
 \begin{equation} \lim_{n \to \infty} \sum_{j=1}^n a_{n,j}^{(k)} x_j = \frac{x}{k}, \qquad \lim_{n \to \infty} \sum_{j=1}^n | a_{n,j}^{(k)}| x_j = \frac{x}{k}. \end{equation}
\begin{equation} \lim_{n \to \infty} \sum_{j=1}^n a_{n,j}^{(k)} x_j = \frac{x}{k}, \qquad \lim_{n \to \infty} \sum_{j=1}^n | a_{n,j}^{(k)}| x_j = \frac{x}{k}. \end{equation}
Proof. Let us define
![]() $A = \{ j \colon \overline{f}_j > 1 \}$
,
$A = \{ j \colon \overline{f}_j > 1 \}$
,
![]() $A_n = A \cap \{ 1, \ldots, n\}$
. First we show that the following conditions (similar to those of the Silverman–Toeplitz theorem) hold:
$A_n = A \cap \{ 1, \ldots, n\}$
. First we show that the following conditions (similar to those of the Silverman–Toeplitz theorem) hold:
-
(i)
 $\lim_{n\to\infty} a_{n,j}^{(k)} = 0$
for all
$\lim_{n\to\infty} a_{n,j}^{(k)} = 0$
for all
 $j\in\mathbb{N}$
;
$j\in\mathbb{N}$
; -
(ii)
 $\lim_{n\to\infty} \sum_{j=1}^n a_{n,j}^{(k)} = {1}/{k}$
;
$\lim_{n\to\infty} \sum_{j=1}^n a_{n,j}^{(k)} = {1}/{k}$
; -
(iii)
 $\sup_{n\in \mathbb{N}} \sum_{j=1}^n | a_{n,j}^{(k)} | < \infty$
;
$\sup_{n\in \mathbb{N}} \sum_{j=1}^n | a_{n,j}^{(k)} | < \infty$
; -
(iv)
 $\lim_{n \to \infty} \sum_{j \in A_n} |a_{n,j}^{(k)} | = 0$
.
$\lim_{n \to \infty} \sum_{j \in A_n} |a_{n,j}^{(k)} | = 0$
.
It is easy to see that (i) holds, as, by (C1),
 \[ |a_{n,j}^{(k)}| = |1 - \overline{f}_j|\prod_{\ell=j+1}^n\overline{f}_\ell^k \leq |1 - \overline{f}_j|\exp\Bigg\{{-}k\sum_{\ell=j+1}^n(1 - \overline{f}_\ell)\Bigg\} \to 0. \]
\[ |a_{n,j}^{(k)}| = |1 - \overline{f}_j|\prod_{\ell=j+1}^n\overline{f}_\ell^k \leq |1 - \overline{f}_j|\exp\Bigg\{{-}k\sum_{\ell=j+1}^n(1 - \overline{f}_\ell)\Bigg\} \to 0. \]
Here and later on, any nonspecified limit relation is meant as
![]() $n \to \infty$
. Since
$n \to \infty$
. Since
 \[ 0 \leq \overline{f}_{0,n} \leq \exp\Bigg\{{-}\sum_{j=1}^n(1-\overline{f}_j)\Bigg\} \to 0, \]
\[ 0 \leq \overline{f}_{0,n} \leq \exp\Bigg\{{-}\sum_{j=1}^n(1-\overline{f}_j)\Bigg\} \to 0, \]
we have
 \[ \sum_{j=1}^n a_{n,j}^{(1)} = \sum_{j=1}^n (1-\overline{f}_j) \overline{f}_{j,n} = \sum_{j=1}^n (\overline{f}_{j,n} - \overline{f}_{j-1,n}) = 1 - \overline{f}_{0,n} \to 1, \]
\[ \sum_{j=1}^n a_{n,j}^{(1)} = \sum_{j=1}^n (1-\overline{f}_j) \overline{f}_{j,n} = \sum_{j=1}^n (\overline{f}_{j,n} - \overline{f}_{j-1,n}) = 1 - \overline{f}_{0,n} \to 1, \]
which is (ii) for
![]() $k = 1$
. Furthermore,
$k = 1$
. Furthermore,
 \[ \sum_{j=1}^n | a_{n,j}^{(1)} | = \sum_{j=1}^n |1-\overline{f}_j| \cdot \overline{f}_{j,n} = \sum_{j=1}^n \left[ (1-\overline{f}_j) + 2 (1 - \overline{f}_j)_- \right] \overline{f}_{j,n} < \infty, \]
\[ \sum_{j=1}^n | a_{n,j}^{(1)} | = \sum_{j=1}^n |1-\overline{f}_j| \cdot \overline{f}_{j,n} = \sum_{j=1}^n \left[ (1-\overline{f}_j) + 2 (1 - \overline{f}_j)_- \right] \overline{f}_{j,n} < \infty, \]
i.e. (iii) holds for
![]() $k = 1$
. Note that
$k = 1$
. Note that
![]() $\sup_{j,n} \overline{f}_{j,n} < \infty$
by (C1). To see (iv), we have
$\sup_{j,n} \overline{f}_{j,n} < \infty$
by (C1). To see (iv), we have
 \[ \sum_{j \in A_n} |a_{n,j}^{(k)} | = \sum_{j=1}^n (\overline{f}_j - 1 )_+ \overline{f}_{j,n}^k \to 0, \]
\[ \sum_{j \in A_n} |a_{n,j}^{(k)} | = \sum_{j=1}^n (\overline{f}_j - 1 )_+ \overline{f}_{j,n}^k \to 0, \]
since
![]() $\lim_{n \to \infty} \overline{f}_{j,n} = 0$
, and
$\lim_{n \to \infty} \overline{f}_{j,n} = 0$
, and
![]() $\big((\overline{f}_j - 1 )_+ \sup_{\ell,n} \overline{f}_{\ell,n}^k\big)_j$
is an integrable majorant, so Lebesgue’s dominated convergence theorem applies.
$\big((\overline{f}_j - 1 )_+ \sup_{\ell,n} \overline{f}_{\ell,n}^k\big)_j$
is an integrable majorant, so Lebesgue’s dominated convergence theorem applies.
Before proving (ii) and (iii) for
![]() $k \geq 2$
we show (7) for
$k \geq 2$
we show (7) for
![]() $k = 1$
. Let
$k = 1$
. Let
![]() $(x_n)_{n\in \mathbb{N}}$
be a sequence with the required properties. Then
$(x_n)_{n\in \mathbb{N}}$
be a sequence with the required properties. Then
 \[ \sum_{j=1}^n a_{n,j}^{(1)} x_j - x = \sum_{j=1}^n a_{n,j}^{(1)}(x_j - x) + x\Bigg(\sum_{j=1}^n a_{n,j}^{(1)} - 1 \Bigg), \]
\[ \sum_{j=1}^n a_{n,j}^{(1)} x_j - x = \sum_{j=1}^n a_{n,j}^{(1)}(x_j - x) + x\Bigg(\sum_{j=1}^n a_{n,j}^{(1)} - 1 \Bigg), \]
where the second term tends to 0 by (ii). For the first term we have
 \[ \begin{split} \Bigg|\sum_{j=1}^n a_{n,j}^{(1)}(x_j -x)\Bigg| & = \Bigg|\sum_{j \in A_n}a_{n,j}^{(1)}(x_j -x) + \sum_{j \not \in A_n}a_{n,j}^{(1)}(x_j -x)\Bigg| \\ & \leq 2\sup_k|x_k| \cdot \sum_{j \in A_n}|a_{n,j}^{(1)}| + \sum_{j \not \in A_n}|a_{n,j}^{(1)}(x_j - x)|, \end{split} \]
\[ \begin{split} \Bigg|\sum_{j=1}^n a_{n,j}^{(1)}(x_j -x)\Bigg| & = \Bigg|\sum_{j \in A_n}a_{n,j}^{(1)}(x_j -x) + \sum_{j \not \in A_n}a_{n,j}^{(1)}(x_j -x)\Bigg| \\ & \leq 2\sup_k|x_k| \cdot \sum_{j \in A_n}|a_{n,j}^{(1)}| + \sum_{j \not \in A_n}|a_{n,j}^{(1)}(x_j - x)|, \end{split} \]
where the first term tends to 0 by (iv), and the second tends to 0 by (i) and (iii). Thus, the first equation in (7) holds for
![]() $k =1$
. Furthermore, since
$k =1$
. Furthermore, since
![]() $a_{j,n}^{(k)} \leq 0$
if and only if
$a_{j,n}^{(k)} \leq 0$
if and only if
![]() $j \in A_n$
, conditions (i)–(iv) remain true for
$j \in A_n$
, conditions (i)–(iv) remain true for
![]() $|a_{n,j}^{(k)}|$
, and thus
$|a_{n,j}^{(k)}|$
, and thus
 \begin{equation} \lim_{n\to \infty} \sum_{j=1}^n |a_{n,j}^{(1)} | x_j = x. \end{equation}
\begin{equation} \lim_{n\to \infty} \sum_{j=1}^n |a_{n,j}^{(1)} | x_j = x. \end{equation}
Next, we prove (ii) and (iii) for arbitrary
![]() $k\geq 2$
. By the binomial theorem,
$k\geq 2$
. By the binomial theorem,
 \begin{equation} 1 - \overline{f}_{0,n}^k = k\sum_{j=1}^n a_{n,j}^{(k)} + \sum_{i=2}^k({-}1)^{i+1}\binom{k}{i}\sum_{j=1}^n(1-\overline{f}_j)^{i-1}a_{n,j}^{(k)}. \end{equation}
\begin{equation} 1 - \overline{f}_{0,n}^k = k\sum_{j=1}^n a_{n,j}^{(k)} + \sum_{i=2}^k({-}1)^{i+1}\binom{k}{i}\sum_{j=1}^n(1-\overline{f}_j)^{i-1}a_{n,j}^{(k)}. \end{equation}
Moreover, for
![]() $i \geq 2$
,
$i \geq 2$
,
 \[ \sum_{j=1}^n|(1-\overline{f}_j)^{i-1}a_{n,j}^{(k)}| = \sum_{j=1}^n|1-\overline{f}_j|^i\overline{f}_{j,n}^k \leq (\sup_{\ell,n}\overline{f}_{\ell,n})^{k-1}\sum_{j=1}^n|a_{n,j}^{(1)}| |1 - \overline{f}_j|^{i-1} \to 0 \]
\[ \sum_{j=1}^n|(1-\overline{f}_j)^{i-1}a_{n,j}^{(k)}| = \sum_{j=1}^n|1-\overline{f}_j|^i\overline{f}_{j,n}^k \leq (\sup_{\ell,n}\overline{f}_{\ell,n})^{k-1}\sum_{j=1}^n|a_{n,j}^{(1)}| |1 - \overline{f}_j|^{i-1} \to 0 \]
by (8). Thus, all the terms in the second sum on the right-hand side of (9) tend to 0. Since
![]() $\overline{f}_{0,n} \to 0$
, (ii) follows. Then (iii) follows as for
$\overline{f}_{0,n} \to 0$
, (ii) follows. Then (iii) follows as for
![]() $k= 1$
. This completes the proof of (ii) and (iii) for
$k= 1$
. This completes the proof of (ii) and (iii) for
![]() $k \geq 2$
. Then (7) for
$k \geq 2$
. Then (7) for
![]() $k \geq 2$
follows exactly as for
$k \geq 2$
follows exactly as for
![]() $k = 1$
.
$k = 1$
.
Lemma 3. Let
![]() $\varphi_n$
be the shape function of
$\varphi_n$
be the shape function of
![]() $f_n$
. Then, under the conditions of Theorem 1 with
$f_n$
. Then, under the conditions of Theorem 1 with
![]() $\nu > 0$
,
$\nu > 0$
,
and the sequence
![]() $\sup_{s\in[0,1]}{|\varphi_n(1)-\varphi_n(s)|}/{|1-\overline{f}_n|}$
is bounded.
$\sup_{s\in[0,1]}{|\varphi_n(1)-\varphi_n(s)|}/{|1-\overline{f}_n|}$
is bounded.
Proof. To ease the notation we suppress the lower index n. By the Taylor expansion,
for some
![]() $ t\in(s,1)$
. Thus, recalling (4), the shape function can be written in the form
$ t\in(s,1)$
. Thus, recalling (4), the shape function can be written in the form
Therefore,
Using the assumptions and the monotonicity of fʹʹʹ, uniformly in
![]() $s \in (0,1]$
,
$s \in (0,1]$
,
thus, convergence on
![]() $\{n\colon\overline{f}_n < 1 \}$
follows.
$\{n\colon\overline{f}_n < 1 \}$
follows.
The boundedness also follows from (10), since if
![]() $\overline{f}_n > 1$
then
$\overline{f}_n > 1$
then
and
![]() $f^{\prime\prime\prime}_n(1)/|1 - \overline{f}_n|$
is bounded by assumption (C3).
$f^{\prime\prime\prime}_n(1)/|1 - \overline{f}_n|$
is bounded by assumption (C3).
3.2. Proof of Theorem 1
Lemma 4. Under the conditions of Theorem 1, for
![]() $s \in [0,1)$
,
$s \in [0,1)$
,
Proof. Recalling (5) and (6), we have to show that
 \[ \overline{f}_{0,n}\varphi_{0,n}(s) = \sum_{j=1}^n\overline{f}_{j-1,n}\varphi_j(f_{j,n}(s)) \to \frac{\nu}{2}. \]
\[ \overline{f}_{0,n}\varphi_{0,n}(s) = \sum_{j=1}^n\overline{f}_{j-1,n}\varphi_j(f_{j,n}(s)) \to \frac{\nu}{2}. \]
First, let
![]() $\nu=0$
. Using Lemmas 1 and 2,
$\nu=0$
. Using Lemmas 1 and 2,
 \[ \overline{f}_{0,n} \varphi_{0,n}(s) \leq \sum_{j=1}^n \overline{f}_{j,n} \frac{f_j^{\prime\prime}(1)}{\overline{f}_j} = \sum_{j=1}^n |a_{n,j}^{(1)} | \frac{f_j^{\prime\prime}(1)}{\overline{f}_j |1-\overline{f}_j|} \to 0. \]
\[ \overline{f}_{0,n} \varphi_{0,n}(s) \leq \sum_{j=1}^n \overline{f}_{j,n} \frac{f_j^{\prime\prime}(1)}{\overline{f}_j} = \sum_{j=1}^n |a_{n,j}^{(1)} | \frac{f_j^{\prime\prime}(1)}{\overline{f}_j |1-\overline{f}_j|} \to 0. \]
If
![]() $\overline{f}_j = 1$
then by (C2) necessarily
$\overline{f}_j = 1$
then by (C2) necessarily
![]() $f_j^{\prime\prime}(1) = 0$
, and
$f_j^{\prime\prime}(1) = 0$
, and
![]() $0/0$
in these types of sums are meant as 0.
$0/0$
in these types of sums are meant as 0.
For
![]() $\nu\in(0,\infty)$
write
$\nu\in(0,\infty)$
write
 \begin{equation} \sum_{j=1}^n \overline{f}_{j-1,n} \varphi_j(f_{j,n}(s)) = \sum_{j=1}^n \overline{f}_{j-1,n} \varphi_j(1) - \sum_{j=1}^n \overline{f}_{j-1,n} (\varphi_j(1) - \varphi_j(f_{j,n}(s))). \end{equation}
\begin{equation} \sum_{j=1}^n \overline{f}_{j-1,n} \varphi_j(f_{j,n}(s)) = \sum_{j=1}^n \overline{f}_{j-1,n} \varphi_j(1) - \sum_{j=1}^n \overline{f}_{j-1,n} (\varphi_j(1) - \varphi_j(f_{j,n}(s))). \end{equation}
By Lemma 2, for the first term we have
 \begin{equation} \sum_{j=1}^n \overline{f}_{j-1,n} \varphi_j(1) = \frac{1}{2} \sum_{j=1}^n a_{n,j}^{(1)} \frac{1}{\overline{f}_j} \frac{f_j^{\prime\prime}(1)}{1- \overline{f}_j} \to \frac{\nu}{2}. \end{equation}
\begin{equation} \sum_{j=1}^n \overline{f}_{j-1,n} \varphi_j(1) = \frac{1}{2} \sum_{j=1}^n a_{n,j}^{(1)} \frac{1}{\overline{f}_j} \frac{f_j^{\prime\prime}(1)}{1- \overline{f}_j} \to \frac{\nu}{2}. \end{equation}
For the second term in (11),
 \[ \Bigg| \sum_{j=1}^n \overline{f}_{j-1,n} (\varphi_j(1) - \varphi_j(f_{j,n}(s))) \Bigg| \leq \sum_{j=1}^{n}a_{n,j}^{(1)}\overline{f}_j\sup_{s\in[0,1]}\frac{|\varphi_j(1)-\varphi_j(s)|}{|1-\overline{f}_j|} \to 0 \]
\[ \Bigg| \sum_{j=1}^n \overline{f}_{j-1,n} (\varphi_j(1) - \varphi_j(f_{j,n}(s))) \Bigg| \leq \sum_{j=1}^{n}a_{n,j}^{(1)}\overline{f}_j\sup_{s\in[0,1]}\frac{|\varphi_j(1)-\varphi_j(s)|}{|1-\overline{f}_j|} \to 0 \]
according to Lemmas 2 and 3. Combining with (11) and (12), the statement follows.
Proof of Theorem 1. We prove the convergence of the conditional g.f. For
![]() $s \in (0,1)$
we have, by the previous lemma,
$s \in (0,1)$
we have, by the previous lemma,
where the limit is the g.f. of the geometric distribution with parameter
![]() ${2}/({2+\nu})$
.
${2}/({2+\nu})$
.
3.3. Proofs of Theorems 2 and 3
We need a strange version of the Riemann approximation, where the points in the partition are not necessarily increasing. It follows immediately from the uniform continuity.
Lemma 5. Assume that
![]() $x_{n,j} \in [0,1]$
,
$x_{n,j} \in [0,1]$
,
![]() $j=0, \ldots, n$
,
$j=0, \ldots, n$
,
![]() $n \in \mathbb{N}$
, such that
$n \in \mathbb{N}$
, such that
![]() $x_{n,0} = 0$
,
$x_{n,0} = 0$
,
![]() $x_{n,n} = 1$
,
$x_{n,n} = 1$
,
![]() $\lim_{n\to\infty}\sup_{j}|x_{n,j} - x_{n,j-1}| = 0$
, and
$\lim_{n\to\infty}\sup_{j}|x_{n,j} - x_{n,j-1}| = 0$
, and
![]() $\sup_n\sum_{j=1}^n|x_{n,j} - x_{n,j-1}| < \infty$
. If f is continuous on [0, 1] then
$\sup_n\sum_{j=1}^n|x_{n,j} - x_{n,j-1}| < \infty$
. If f is continuous on [0, 1] then
 \[ \lim_{n\to\infty}\sum_{j=1}^n f(u_{n,j})(x_{n,j} - x_{n,j-1}) = \int_0^1 f(x) \, \textrm{d}x, \]
\[ \lim_{n\to\infty}\sum_{j=1}^n f(u_{n,j})(x_{n,j} - x_{n,j-1}) = \int_0^1 f(x) \, \textrm{d}x, \]
with
![]() $u_{n,j} \in [\min (x_{n,j-1}, x_{n,j}), \max(x_{n,j-1}, x_{n,j})]$
.
$u_{n,j} \in [\min (x_{n,j-1}, x_{n,j}), \max(x_{n,j-1}, x_{n,j})]$
.
We also need a simple lemma on an alternating sum involving binomial coefficients.
Lemma 6. For
![]() $x\in\mathbb{R}$
,
$x\in\mathbb{R}$
,
 \[ \sum_{i=1}^{k-1}\binom{k-1}{i}({-}1)^{i}\frac{(1+x)^i-1}{i} = \sum_{i=1}^{k-1}({-}1)^{i}\frac{x^i}{i}. \]
\[ \sum_{i=1}^{k-1}\binom{k-1}{i}({-}1)^{i}\frac{(1+x)^i-1}{i} = \sum_{i=1}^{k-1}({-}1)^{i}\frac{x^i}{i}. \]
Proof. Both sides are polynomials of x, and equality holds for
![]() $x = 0$
, therefore it is enough to show that the derivatives are equal. Differentiating the left-hand side we obtain
$x = 0$
, therefore it is enough to show that the derivatives are equal. Differentiating the left-hand side we obtain
 \[ \sum_{i=1}^{k-1}\binom{k-1}{i}({-}1)^i(1+x)^{i-1} = \frac{1}{1+x}[(1 - (1+x))^{k-1} - 1]. \]
\[ \sum_{i=1}^{k-1}\binom{k-1}{i}({-}1)^i(1+x)^{i-1} = \frac{1}{1+x}[(1 - (1+x))^{k-1} - 1]. \]
Differentiating the right-hand side and multiplying by
![]() $(1+x)$
, the statement follows.
$(1+x)$
, the statement follows.
The next statement is an easy consequence of the Taylor expansion of the g.f.
Lemma 7. ([Reference Györfi, Ispány, Pap and Varga12, Lemma 6].) Let
![]() $\varepsilon$
be a nonnegative integer-valued random variable with factorial moments
$\varepsilon$
be a nonnegative integer-valued random variable with factorial moments
![]() $m_{k} \;:\!=\; \mathbb{E}[\varepsilon(\varepsilon-1)\cdots(\varepsilon-k+1)]$
,
$m_{k} \;:\!=\; \mathbb{E}[\varepsilon(\varepsilon-1)\cdots(\varepsilon-k+1)]$
,
![]() $k\in \mathbb{N}$
,
$k\in \mathbb{N}$
,
![]() $m_{0} \;:\!=\; 1$
, and with g.f.
$m_{0} \;:\!=\; 1$
, and with g.f.
![]() $h(s) = \mathbb{E}s^{\varepsilon}$
,
$h(s) = \mathbb{E}s^{\varepsilon}$
,
![]() $s\in[-1,1]$
. If
$s\in[-1,1]$
. If
![]() $m_{\ell}<\infty$
for some
$m_{\ell}<\infty$
for some
![]() $\ell \in \mathbb{N}$
with
$\ell \in \mathbb{N}$
with
![]() $|s|\leq 1$
, then
$|s|\leq 1$
, then
 \[ h(s) = \sum_{k=0}^{\ell-1}\frac{m_{k}}{k!}(s-1)^k + R_{\ell}(s), \qquad |R_{\ell}(s)| \leq \frac{m_{\ell}}{\ell!}|s-1|^\ell. \]
\[ h(s) = \sum_{k=0}^{\ell-1}\frac{m_{k}}{k!}(s-1)^k + R_{\ell}(s), \qquad |R_{\ell}(s)| \leq \frac{m_{\ell}}{\ell!}|s-1|^\ell. \]
Proof of Theorem 2. Recall that
![]() $f_n(s)=\mathbb{E}s^{\xi_n}$
, and let
$f_n(s)=\mathbb{E}s^{\xi_n}$
, and let
![]() $g_n(s)=\mathbb{E}s^{Y_n}$
and
$g_n(s)=\mathbb{E}s^{Y_n}$
and
![]() $h_n(s)=\mathbb{E} s^{\varepsilon_n}$
. Then the branching property gives (see, e.g., [Reference González, Kersting, Minuesa and del Puerto9, Proposition 1])
$h_n(s)=\mathbb{E} s^{\varepsilon_n}$
. Then the branching property gives (see, e.g., [Reference González, Kersting, Minuesa and del Puerto9, Proposition 1])
![]() $g_n(s)=\prod_{j=1}^{n}h_j(f_{j,n}(s))$
. We prove the convergence of the g.f., i.e.
$g_n(s)=\prod_{j=1}^{n}h_j(f_{j,n}(s))$
. We prove the convergence of the g.f., i.e.
![]() $\lim_{n \to \infty } g_n(s) = f_Y(s)$
,
$\lim_{n \to \infty } g_n(s) = f_Y(s)$
,
![]() $s \in [0,1]$
. Fix
$s \in [0,1]$
. Fix
![]() $s \in [0,1)$
, and introduce
$s \in [0,1)$
, and introduce
![]() $\widehat{g}_n(s)=\prod_{j=1}^{n}\textrm{e}^{h_j(f_{j,n}(s))-1}$
. Note that
$\widehat{g}_n(s)=\prod_{j=1}^{n}\textrm{e}^{h_j(f_{j,n}(s))-1}$
. Note that
![]() $\widehat g_n$
is a kind of accompanying law, its distribution is compound-Poisson, and therefore its limit is compound-Poisson too [Reference Steutel and van Harn19, Proposition 2.2]. By the convexity of the g.f.,
$\widehat g_n$
is a kind of accompanying law, its distribution is compound-Poisson, and therefore its limit is compound-Poisson too [Reference Steutel and van Harn19, Proposition 2.2]. By the convexity of the g.f.,
If
![]() $|a_k|, |b_k|< 1$
,
$|a_k|, |b_k|< 1$
,
![]() $k=1,\ldots, n$
, then
$k=1,\ldots, n$
, then
 \begin{equation*} \Bigg|\prod_{k=1}^{n}a_k - \prod_{k=1}^{n}b_k\Bigg| \leq \sum_{k=1}^{n}| a_k-b_k|. \end{equation*}
\begin{equation*} \Bigg|\prod_{k=1}^{n}a_k - \prod_{k=1}^{n}b_k\Bigg| \leq \sum_{k=1}^{n}| a_k-b_k|. \end{equation*}
Consequently, using the latter inequality, the inequalities
![]() $|\textrm{e}^u-1-u|\leq u^2$
for
$|\textrm{e}^u-1-u|\leq u^2$
for
![]() $|u| \leq 1$
and
$|u| \leq 1$
and
![]() $0\leq 1-h_j(s)\leq m_{j,1}(1-s)$
, and (13), we have
$0\leq 1-h_j(s)\leq m_{j,1}(1-s)$
, and (13), we have
 \begin{align} |g_n(s)-\widehat{g}_n(s)| & \leq \sum_{j=1}^{n}|\textrm{e}^{h_j(f_{j,n}(s))-1}-h_j(f_{j,n}(s))| \nonumber \\ & \leq \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1)^2\leq \sum_{j=1}^{n}\frac{m_{j,1}^2}{|1-\overline{f}_j|}|a_{n,j}^{(2)}|\to 0, \end{align}
\begin{align} |g_n(s)-\widehat{g}_n(s)| & \leq \sum_{j=1}^{n}|\textrm{e}^{h_j(f_{j,n}(s))-1}-h_j(f_{j,n}(s))| \nonumber \\ & \leq \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1)^2\leq \sum_{j=1}^{n}\frac{m_{j,1}^2}{|1-\overline{f}_j|}|a_{n,j}^{(2)}|\to 0, \end{align}
where we used Lemma 2, since
Therefore, we need to show that
 \begin{equation} \lim_{n\to \infty} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) = \log f_Y(s). \end{equation}
\begin{equation} \lim_{n\to \infty} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) = \log f_Y(s). \end{equation}
By Lemma 7,
 \begin{equation} h_j(s)= \sum_{k=0}^{K-1} \frac{m_{j,k}}{k!}(s-1)^k + R_{j,K}(s), \end{equation}
\begin{equation} h_j(s)= \sum_{k=0}^{K-1} \frac{m_{j,k}}{k!}(s-1)^k + R_{j,K}(s), \end{equation}
where
![]() $|R_{j,K}(s)| \leq ({m_{j,K}}/{K!})(1-s)^K$
, and thus
$|R_{j,K}(s)| \leq ({m_{j,K}}/{K!})(1-s)^K$
, and thus
 \begin{align} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) & = \sum_{j=1}^{n}\Bigg[\sum_{k=1}^{K-1}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k + R_{j,K}(f_{j,n}(s))\Bigg] \nonumber \\ & = \sum_{k=1}^{K-1}{({-}1)^k}\sum_{j=1}^{n}\frac{m_{j,k}}{k!(1 - \overline{f}_j)}a_{n,j}^{(k)} \bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k + \sum_{j=1}^{n}R_{j,K}(f_{j,n}(s)). \end{align}
\begin{align} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) & = \sum_{j=1}^{n}\Bigg[\sum_{k=1}^{K-1}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k + R_{j,K}(f_{j,n}(s))\Bigg] \nonumber \\ & = \sum_{k=1}^{K-1}{({-}1)^k}\sum_{j=1}^{n}\frac{m_{j,k}}{k!(1 - \overline{f}_j)}a_{n,j}^{(k)} \bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k + \sum_{j=1}^{n}R_{j,K}(f_{j,n}(s)). \end{align}
 \begin{align} \Bigg|\sum_{j=1}^{n} R_{j,K}(f_{j,n}(s))\Bigg| & \leq \sum_{j=1}^{n}\frac{m_{j,K}}{K!}|f_{j,n}(s)-1|^K \nonumber \\ & \leq \sum_{j=1}^{n}\frac{m_{j,K}}{K!}\overline{f}_{j,n}^K(1-s)^K = (1-s)^K\sum_{j=1}^{n}\frac{m_{j,K}}{K!|1-\overline{f}_j|}|a_{n,j}^{(K)}| \to 0. \end{align}
\begin{align} \Bigg|\sum_{j=1}^{n} R_{j,K}(f_{j,n}(s))\Bigg| & \leq \sum_{j=1}^{n}\frac{m_{j,K}}{K!}|f_{j,n}(s)-1|^K \nonumber \\ & \leq \sum_{j=1}^{n}\frac{m_{j,K}}{K!}\overline{f}_{j,n}^K(1-s)^K = (1-s)^K\sum_{j=1}^{n}\frac{m_{j,K}}{K!|1-\overline{f}_j|}|a_{n,j}^{(K)}| \to 0. \end{align}
Up to this point, everything works for
![]() $\nu \geq 0$
. Now assume that
$\nu \geq 0$
. Now assume that
![]() $\nu > 0$
. Then, by Lemmas 2 and 3,
$\nu > 0$
. Then, by Lemmas 2 and 3,
 \begin{equation} \Bigg|\sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(1)-\varphi_i(f_{i,n}(s))}{1-\overline{f}_i}\Bigg| \leq \sup_{k\geq1}\overline{f}_k\sum_{i=1}^n|a_{n,i}^{(1)}| \sup_{t\in[0,1]}\frac{|\varphi_i(1)-\varphi_i(t)|}{|1-\overline{f}_i|} \to 0, \end{equation}
\begin{equation} \Bigg|\sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(1)-\varphi_i(f_{i,n}(s))}{1-\overline{f}_i}\Bigg| \leq \sup_{k\geq1}\overline{f}_k\sum_{i=1}^n|a_{n,i}^{(1)}| \sup_{t\in[0,1]}\frac{|\varphi_i(1)-\varphi_i(t)|}{|1-\overline{f}_i|} \to 0, \end{equation}
and similarly
 \begin{equation} \Bigg|\sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(1)}{1-\overline{f}_i} - \frac{\nu}{2}\sum_{i=j+1}^{n}a_{n,i}^{(1)}\Bigg| \leq \sum_{i=1}^{n}|a_{n,i}^{(1)}|\bigg|\frac{1}{\overline{f}_i} \frac{f_i^{\prime\prime}(1)}{2(1-\overline{f}_i)}-\frac{\nu}{2}\bigg| \to 0. \end{equation}
\begin{equation} \Bigg|\sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(1)}{1-\overline{f}_i} - \frac{\nu}{2}\sum_{i=j+1}^{n}a_{n,i}^{(1)}\Bigg| \leq \sum_{i=1}^{n}|a_{n,i}^{(1)}|\bigg|\frac{1}{\overline{f}_i} \frac{f_i^{\prime\prime}(1)}{2(1-\overline{f}_i)}-\frac{\nu}{2}\bigg| \to 0. \end{equation}
Putting
 \begin{equation} \varepsilon_{j,n} = \sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(f_{i,n}(s))}{1-\overline{f}_i} - \frac{\nu}{2}(1 - \overline{f}_{j,n}), \end{equation}
\begin{equation} \varepsilon_{j,n} = \sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(f_{i,n}(s))}{1-\overline{f}_i} - \frac{\nu}{2}(1 - \overline{f}_{j,n}), \end{equation}
 \begin{equation} \frac{\overline{f}_{j,n}}{1-f_{j,n}(s)} = \frac{1}{1 - s} + \sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(f_{i,n}(s))}{1-\overline{f}_i} = \frac{1}{1-s} + \frac{\nu}{2}(1 - \overline{f}_{j,n}) + \varepsilon_{j,n}. \end{equation}
\begin{equation} \frac{\overline{f}_{j,n}}{1-f_{j,n}(s)} = \frac{1}{1 - s} + \sum_{i=j+1}^{n}a_{n,i}^{(1)}\overline{f}_i\frac{\varphi_i(f_{i,n}(s))}{1-\overline{f}_i} = \frac{1}{1-s} + \frac{\nu}{2}(1 - \overline{f}_{j,n}) + \varepsilon_{j,n}. \end{equation}
Noting that
![]() $\sum_{i=j+1}^{n}a_{n,i}^{(1)} = 1-\overline{f}_{j,n}$
, (19), (20), and the triangle inequality imply that, for
$\sum_{i=j+1}^{n}a_{n,i}^{(1)} = 1-\overline{f}_{j,n}$
, (19), (20), and the triangle inequality imply that, for
![]() $\varepsilon_{j,n}$
in (21),
$\varepsilon_{j,n}$
in (21),
The latter further implies that
and that for n large enough, by the mean value theorem and (22),
Thus, by (24),
 \begin{align} \Bigg|\sum_{j=1}^{n}a_{n,j}^{(k)} & \bigg[\frac{m_{j,k}}{k!(1 - \overline{f}_j)}\bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k - \lambda_k\bigg(\frac{1}{1-s} + \frac{\nu}{2}{(1 - \overline{f}_{j,n})}\bigg)^{-k}\bigg]\Bigg| \nonumber \\ & \leq \sum_{j=1}^{n}|a_{n,j}^{(k)}|\Bigg[ \bigg|\frac{m_{j,k}}{k!(1 - \overline{f}_j)} - \lambda_k\bigg| \bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k \nonumber \\ & \qquad\qquad\qquad + \lambda_k\bigg|\bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k - \bigg(\frac{1}{1-s} + \frac{\nu}{2}{(1 - \overline{f}_{j,n})}\bigg)^{-k}\bigg|\Bigg] \nonumber \\ & \leq \sum_{j=1}^{n}|a_{n,j}^{(k)}|\bigg|\frac{m_{j,k}}{k!(1 - \overline{f}_j)} - \lambda_k\bigg| + \lambda_k\sum_{j=1}^{n}|a_{n,j}^{(k)}|k\max_{j\leq n}\varepsilon_{j,n} \to 0, \end{align}
\begin{align} \Bigg|\sum_{j=1}^{n}a_{n,j}^{(k)} & \bigg[\frac{m_{j,k}}{k!(1 - \overline{f}_j)}\bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k - \lambda_k\bigg(\frac{1}{1-s} + \frac{\nu}{2}{(1 - \overline{f}_{j,n})}\bigg)^{-k}\bigg]\Bigg| \nonumber \\ & \leq \sum_{j=1}^{n}|a_{n,j}^{(k)}|\Bigg[ \bigg|\frac{m_{j,k}}{k!(1 - \overline{f}_j)} - \lambda_k\bigg| \bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k \nonumber \\ & \qquad\qquad\qquad + \lambda_k\bigg|\bigg(\frac{1 - f_{j,n}(s)}{\overline{f}_{j,n}}\bigg)^k - \bigg(\frac{1}{1-s} + \frac{\nu}{2}{(1 - \overline{f}_{j,n})}\bigg)^{-k}\bigg|\Bigg] \nonumber \\ & \leq \sum_{j=1}^{n}|a_{n,j}^{(k)}|\bigg|\frac{m_{j,k}}{k!(1 - \overline{f}_j)} - \lambda_k\bigg| + \lambda_k\sum_{j=1}^{n}|a_{n,j}^{(k)}|k\max_{j\leq n}\varepsilon_{j,n} \to 0, \end{align}
where the second inequality holds for n large enough.
Furthermore, by Lemma 5,
 \begin{equation} \lim_{n\to\infty}\sum_{j=1}^{n}a_{n,j}^{(k)}\bigg(\frac{1}{1-s}+\frac{\nu}{2}(1-\overline{f}_{j,n})\bigg)^{-k} = \int_{0}^{1}\frac{y^{k-1}}{({1}/({1-s})+({\nu}/{2})(1-y))^k}\,\textrm{d}y, \end{equation}
\begin{equation} \lim_{n\to\infty}\sum_{j=1}^{n}a_{n,j}^{(k)}\bigg(\frac{1}{1-s}+\frac{\nu}{2}(1-\overline{f}_{j,n})\bigg)^{-k} = \int_{0}^{1}\frac{y^{k-1}}{({1}/({1-s})+({\nu}/{2})(1-y))^k}\,\textrm{d}y, \end{equation}
since the left-hand side is a Riemann approximation of the right-hand side corresponding to the partition
![]() $\{\overline{f}_{j,n}\}_{j=-1}^n$
, with
$\{\overline{f}_{j,n}\}_{j=-1}^n$
, with
![]() $\overline{f}_{-1,n} \;:\!=\; 0$
and
$\overline{f}_{-1,n} \;:\!=\; 0$
and
![]() $\overline{f}_{j,n} - \overline{f}_{j-1,n} = a_{n,j}^{(1)}\to 0$
uniformly in j according to Lemma 2, while
$\overline{f}_{j,n} - \overline{f}_{j-1,n} = a_{n,j}^{(1)}\to 0$
uniformly in j according to Lemma 2, while
![]() $\overline{f}_{0,n} \to 0$
by (C1). Changing variables
$\overline{f}_{0,n} \to 0$
by (C1). Changing variables
![]() $u=\nu (1-s)(1-y)+2$
and using the binomial theorem,
$u=\nu (1-s)(1-y)+2$
and using the binomial theorem,
 \begin{align} \int_{0}^{1} & \frac{y^{k-1}}{({1}/({1-s})+({\nu}/{2})(1-y))^k}\,\textrm{d}y \nonumber \\ & = 2^k(1-s)^k\int_{0}^{1}\frac{y^{k-1}}{(2+\nu(1-s)(1-y))^k}\,\textrm{d}y \nonumber \\ & = \frac{2^k}{\nu^k}\int_{2}^{\nu(1-s)+2}\frac{(2+\nu(1-s)-u)^{k-1}}{u^k}\,\textrm{d}u \nonumber \\ & = \frac{2^k}{\nu^k}\int_2^{\nu(1-s)+2}\frac{1}{u^k} \sum_{i=0}^{k-1}\bigg[\binom{k-1}{i}(2+\nu(1-s))^i({-}u)^{k-1-i}\bigg]\,\textrm{d}u \nonumber \\ & = \frac{2^k}{\nu^k}\sum_{i=0}^{k-1}\bigg[\binom{k-1}{i}(2+\nu(1-s))^i ({-}1)^{k-1-i}\int_2^{\nu(1-s)+2}u^{-(i+1)}\,\textrm{d}u\bigg] \nonumber \\ & = ({-}1)^{k+1}\frac{2^k}{\nu^k}\bigg(\log\bigg(1+\frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}\binom{k-1}{i}({-}1)^{i}\frac{(1+({\nu}/{2})(1-s))^{i}-1}{i}\bigg) \nonumber \\ & = ({-}1)^{k+1}\frac{2^k}{\nu^k}\Bigg( \log\bigg(1+\frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i\Bigg), \end{align}
\begin{align} \int_{0}^{1} & \frac{y^{k-1}}{({1}/({1-s})+({\nu}/{2})(1-y))^k}\,\textrm{d}y \nonumber \\ & = 2^k(1-s)^k\int_{0}^{1}\frac{y^{k-1}}{(2+\nu(1-s)(1-y))^k}\,\textrm{d}y \nonumber \\ & = \frac{2^k}{\nu^k}\int_{2}^{\nu(1-s)+2}\frac{(2+\nu(1-s)-u)^{k-1}}{u^k}\,\textrm{d}u \nonumber \\ & = \frac{2^k}{\nu^k}\int_2^{\nu(1-s)+2}\frac{1}{u^k} \sum_{i=0}^{k-1}\bigg[\binom{k-1}{i}(2+\nu(1-s))^i({-}u)^{k-1-i}\bigg]\,\textrm{d}u \nonumber \\ & = \frac{2^k}{\nu^k}\sum_{i=0}^{k-1}\bigg[\binom{k-1}{i}(2+\nu(1-s))^i ({-}1)^{k-1-i}\int_2^{\nu(1-s)+2}u^{-(i+1)}\,\textrm{d}u\bigg] \nonumber \\ & = ({-}1)^{k+1}\frac{2^k}{\nu^k}\bigg(\log\bigg(1+\frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}\binom{k-1}{i}({-}1)^{i}\frac{(1+({\nu}/{2})(1-s))^{i}-1}{i}\bigg) \nonumber \\ & = ({-}1)^{k+1}\frac{2^k}{\nu^k}\Bigg( \log\bigg(1+\frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i\Bigg), \end{align}
where the last equality follows from Lemma 6. Substituting back into (17), by (18), (25), (26), and (27) we obtain (15).
To finish the proof we need to handle the
![]() $\nu = 0$
case. Then the calculations are easier. We can still define
$\nu = 0$
case. Then the calculations are easier. We can still define
![]() $\varepsilon_{j,n}$
as in (21), and (20) remains true. Applying Lemma 1, we see that (23) and (24) hold true as well, therefore (25) follows with
$\varepsilon_{j,n}$
as in (21), and (20) remains true. Applying Lemma 1, we see that (23) and (24) hold true as well, therefore (25) follows with
![]() $\nu = 0$
everywhere. There is no need for the Riemann approximation, (15) follows from Lemma 2.
$\nu = 0$
everywhere. There is no need for the Riemann approximation, (15) follows from Lemma 2.
Proof of Theorem 3. Here we consider only the
![]() $\nu > 0$
case. For
$\nu > 0$
case. For
![]() $\nu = 0$
the calculations are easier, and follow similarly to the previous proof.
$\nu = 0$
the calculations are easier, and follow similarly to the previous proof.
Similarly to the proof of Theorem 2, (14) holds, so it is enough to prove that
 \begin{equation*} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) \to \log f_Y(s). \end{equation*}
\begin{equation*} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) \to \log f_Y(s). \end{equation*}
Fix
![]() $s\in(0,1)$
. By Taylor’s theorem, for some
$s\in(0,1)$
. By Taylor’s theorem, for some
![]() $\xi \in (0, \nu(1-s)/2)$
,
$\xi \in (0, \nu(1-s)/2)$
,
 \[ \log\bigg(1+\frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i = \frac{\nu^k(1-s)^k}{2^k}\frac{1}{(1 + \xi)^k}\frac{1}{k}, \]
\[ \log\bigg(1+\frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i = \frac{\nu^k(1-s)^k}{2^k}\frac{1}{(1 + \xi)^k}\frac{1}{k}, \]
so
 \[ \frac{2^k}{\nu^{k}}\Bigg|\log\bigg(1+\frac{\nu}{2} (1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i\Bigg| \leq \frac{(1-s)^k}{k}. \]
\[ \frac{2^k}{\nu^{k}}\Bigg|\log\bigg(1+\frac{\nu}{2} (1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i\Bigg| \leq \frac{(1-s)^k}{k}. \]
Therefore, for any
![]() $\varepsilon > 0$
there exists
$\varepsilon > 0$
there exists
![]() $\ell$
large enough such that
$\ell$
large enough such that
 \begin{equation} \Bigg|\sum_{k=\ell}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1 + \frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i\Bigg)\Bigg| \leq \sum_{k=\ell}^\infty\frac{\lambda_k(1-s)^k}{k} < \varepsilon. \end{equation}
\begin{equation} \Bigg|\sum_{k=\ell}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1 + \frac{\nu}{2}(1-s)\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}(1-s)^i\Bigg)\Bigg| \leq \sum_{k=\ell}^\infty\frac{\lambda_k(1-s)^k}{k} < \varepsilon. \end{equation}
By Lemma 7, (16) holds with
![]() $K = \ell$
and therefore
$K = \ell$
and therefore
 \[ \begin{split} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) & = \sum_{j=1}^{n}\Bigg[\sum_{k=1}^{\ell-1}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k + R_{j,\ell}(f_{j,n}(s))\Bigg] \\ & = \sum_{k=1}^{\ell-1}\sum_{j=1}^{n}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k + \sum_{j=1}^{n}R_{j,\ell}(f_{j,n}(s)). \end{split} \]
\[ \begin{split} \sum_{j=1}^{n}(h_j(f_{j,n}(s))-1) & = \sum_{j=1}^{n}\Bigg[\sum_{k=1}^{\ell-1}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k + R_{j,\ell}(f_{j,n}(s))\Bigg] \\ & = \sum_{k=1}^{\ell-1}\sum_{j=1}^{n}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k + \sum_{j=1}^{n}R_{j,\ell}(f_{j,n}(s)). \end{split} \]
Moreover, by (13) and Lemma 2,
 \begin{equation} \Bigg|\sum_{j=1}^{n}R_{j,\ell}(f_{j,n}(s))\Bigg| \leq \sum_{j=1}^{n}\frac{m_{j,\ell}}{\ell!}|f_{j,n}(s)-1|^\ell \leq \sum_{j=1}^{n}\frac{m_{j,\ell}}{\ell!}\overline{f}_{j,n}^\ell(1-s)^\ell \to \frac{(1-s)^\ell}{\ell}\lambda_\ell \leq \varepsilon. \end{equation}
\begin{equation} \Bigg|\sum_{j=1}^{n}R_{j,\ell}(f_{j,n}(s))\Bigg| \leq \sum_{j=1}^{n}\frac{m_{j,\ell}}{\ell!}|f_{j,n}(s)-1|^\ell \leq \sum_{j=1}^{n}\frac{m_{j,\ell}}{\ell!}\overline{f}_{j,n}^\ell(1-s)^\ell \to \frac{(1-s)^\ell}{\ell}\lambda_\ell \leq \varepsilon. \end{equation}
Summarizing,
 \begin{align*} \Bigg|\sum_{j=1}^n(h_j(f_{j,n}(s)) & - 1) - \log f_Y(s)\Bigg| \\ & \leq \Bigg|\sum_{k=1}^{\ell-1}\sum_{j=1}^{n}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k \\ & \qquad + \sum_{k=1}^{\ell-1}\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1+\frac{\nu}{2}(1-s)\bigg) - \sum_{i=1}^{k-1}({-}1)^{i+1}\frac{\nu^i}{i2^i}(1-s)^i\Bigg)\Bigg| \\ & \quad + \Bigg|\sum_{k=\ell}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1+\frac{\nu}{2}(1-s)\bigg)-\sum_{i=1}^{k-1}({-}1)^{i+1}\frac{\nu^i}{i2^i}(1-s)^i\Bigg)\Bigg| \\ & \quad + \Bigg|\sum_{j=1}^{n}R_{j,\ell}(f_{j,n}(s))\Bigg|, \end{align*}
\begin{align*} \Bigg|\sum_{j=1}^n(h_j(f_{j,n}(s)) & - 1) - \log f_Y(s)\Bigg| \\ & \leq \Bigg|\sum_{k=1}^{\ell-1}\sum_{j=1}^{n}\frac{m_{j,k}}{k!}(f_{j,n}(s)-1)^k \\ & \qquad + \sum_{k=1}^{\ell-1}\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1+\frac{\nu}{2}(1-s)\bigg) - \sum_{i=1}^{k-1}({-}1)^{i+1}\frac{\nu^i}{i2^i}(1-s)^i\Bigg)\Bigg| \\ & \quad + \Bigg|\sum_{k=\ell}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1+\frac{\nu}{2}(1-s)\bigg)-\sum_{i=1}^{k-1}({-}1)^{i+1}\frac{\nu^i}{i2^i}(1-s)^i\Bigg)\Bigg| \\ & \quad + \Bigg|\sum_{j=1}^{n}R_{j,\ell}(f_{j,n}(s))\Bigg|, \end{align*}
where the first term on the right-hand side converges to 0 by the previous result, while the second and third terms are small for n large by (28) and (29). As
![]() $\varepsilon > 0$
is arbitrary, the proof is complete.
$\varepsilon > 0$
is arbitrary, the proof is complete.
3.4. Proof of Theorem 4
Before the proof, we need two auxiliary lemmas.
Lemma 8. If condition (C4) of Theorem 2 or (C4ʹ) of Theorem 3 hold, then
exists for each
![]() $i = 1,2,\ldots$
$i = 1,2,\ldots$
Proof. Without loss of generality we assume that
![]() $\overline{f}_n < 1$
for each n. Otherwise, simply consider everything on the subsequence
$\overline{f}_n < 1$
for each n. Otherwise, simply consider everything on the subsequence
![]() $\{n\colon\overline{f}_n < 1 \}$
.
$\{n\colon\overline{f}_n < 1 \}$
.
Let
![]() $h_n[i] = \mathbb{P}(\varepsilon_n = i)$
. If (C4) holds, there are only finitely many
$h_n[i] = \mathbb{P}(\varepsilon_n = i)$
. If (C4) holds, there are only finitely many
![]() $\lambda$
s, and the statement follows easily by backward induction. However, if (C4ʹ) holds, a more involved argument is needed, which works in both cases.
$\lambda$
s, and the statement follows easily by backward induction. However, if (C4ʹ) holds, a more involved argument is needed, which works in both cases.
The kth moment of a random variable can be expressed in terms of its factorial moments as
 \[ \mu_{n,k} \;:\!=\; \mathbb{E} \varepsilon_n^k = \sum_{i=1}^k \genfrac\{\}{0pt}{0}{k}{i} m_{n,i}, \]
\[ \mu_{n,k} \;:\!=\; \mathbb{E} \varepsilon_n^k = \sum_{i=1}^k \genfrac\{\}{0pt}{0}{k}{i} m_{n,i}, \]
where
 $$\genfrac\{\}{0pt}{0}{k}{i} = \frac{1}{i!}\sum_{j=0}^i({-}1)^j\binom{i}{j}(i-j)^k$$
$$\genfrac\{\}{0pt}{0}{k}{i} = \frac{1}{i!}\sum_{j=0}^i({-}1)^j\binom{i}{j}(i-j)^k$$
denotes the Stirling number of the second kind; on Stirling numbers, see [Reference Graham, Knuth and Patashnik10, Section 6.1]. Therefore,
 \begin{equation} \sum_{i=1}^\infty\frac{i^k h_n[i]}{1-\overline{f}_n} = \frac{\mu_{n,k}}{1-\overline{f}_n} = \sum_{i=1}^k\genfrac\{\}{0pt}{0}{k}{i}\frac{m_{n,i}}{1-\overline{f}_n} \to \sum_{i=1}^k\genfrac\{\}{0pt}{0}{k}{i}i!\lambda_i \;=\!:\; \mu_k. \end{equation}
\begin{equation} \sum_{i=1}^\infty\frac{i^k h_n[i]}{1-\overline{f}_n} = \frac{\mu_{n,k}}{1-\overline{f}_n} = \sum_{i=1}^k\genfrac\{\}{0pt}{0}{k}{i}\frac{m_{n,i}}{1-\overline{f}_n} \to \sum_{i=1}^k\genfrac\{\}{0pt}{0}{k}{i}i!\lambda_i \;=\!:\; \mu_k. \end{equation}
Hence, the sequence
![]() $(h_n[i]/(1- \overline f_n))_{n\in\mathbb{N}}$
is bounded in n for all i. Therefore, any subsequence contains a further subsequence
$(h_n[i]/(1- \overline f_n))_{n\in\mathbb{N}}$
is bounded in n for all i. Therefore, any subsequence contains a further subsequence
![]() $(n_\ell)$
such that
$(n_\ell)$
such that
To prove the statement we have to show that the sequence
![]() $(q_i)$
is unique, it does not depend on the subsequence. Note that the sequence
$(q_i)$
is unique, it does not depend on the subsequence. Note that the sequence
![]() $(q_i)_{i\in\mathbb{N}}$
is not necessarily a probability distribution.
$(q_i)_{i\in\mathbb{N}}$
is not necessarily a probability distribution.
By Fatou’s lemma and (30),
Let
![]() $\varepsilon > 0$
and
$\varepsilon > 0$
and
![]() $k \in \mathbb{N}$
be arbitrary. Write
$k \in \mathbb{N}$
be arbitrary. Write
![]() $n_\ell = n$
, and put
$n_\ell = n$
, and put
![]() $K \;:\!=\; \lfloor{\mu_{k+1}}/{\varepsilon}\rfloor + 1$
, with
$K \;:\!=\; \lfloor{\mu_{k+1}}/{\varepsilon}\rfloor + 1$
, with
![]() $\lfloor\cdot\rfloor$
representing the lower integer part. Then
$\lfloor\cdot\rfloor$
representing the lower integer part. Then
and hence, by (30) and the definition of K,
Therefore, by (31),
 \[ \mu_{k} = \lim_{n\to\infty}\sum_{i=1}^\infty\frac{h_n[i]}{1 - \overline f_n}i^{k} \leq \limsup_{n\to\infty}\sum_{i=1}^K\frac{h_n[i]}{1 - \overline f_n}i^k + \varepsilon \leq \sum_{i=1}^\infty q_i i^k + \varepsilon. \]
\[ \mu_{k} = \lim_{n\to\infty}\sum_{i=1}^\infty\frac{h_n[i]}{1 - \overline f_n}i^{k} \leq \limsup_{n\to\infty}\sum_{i=1}^K\frac{h_n[i]}{1 - \overline f_n}i^k + \varepsilon \leq \sum_{i=1}^\infty q_i i^k + \varepsilon. \]
Since
![]() $\varepsilon > 0$
is arbitrary, by (32),
$\varepsilon > 0$
is arbitrary, by (32),
Using the Stieltjes moment problem we show that the sequence
![]() $(\mu_k)$
uniquely determines
$(\mu_k)$
uniquely determines
![]() $(q_i)$
. In order to do that, it is enough to show that Carleman’s condition [Reference Simon18, Theorem 5.6.6] is fulfilled, i.e.
$(q_i)$
. In order to do that, it is enough to show that Carleman’s condition [Reference Simon18, Theorem 5.6.6] is fulfilled, i.e.
![]() $\mu_k$
is not too large. Since
$\mu_k$
is not too large. Since
![]() $\limsup_{n\to\infty}\lambda_n^{1/n} \leq 1$
, for n large,
$\limsup_{n\to\infty}\lambda_n^{1/n} \leq 1$
, for n large,
![]() $\lambda_n \leq 2^n$
. Furthermore, by trivial upper bounds,
$\lambda_n \leq 2^n$
. Furthermore, by trivial upper bounds,
 \[ \genfrac\{\}{0pt}{0}{k}{i}i! = \sum_{\ell=0}^i({-}1)^\ell\binom{i}{\ell}(i - \ell)^k \leq i^k 2^i, \]
\[ \genfrac\{\}{0pt}{0}{k}{i}i! = \sum_{\ell=0}^i({-}1)^\ell\binom{i}{\ell}(i - \ell)^k \leq i^k 2^i, \]
and thus, by (30), for some
![]() $C >0$
,
$C >0$
,
 \[ \mu_k = \sum_{i=0}^k\genfrac\{\}{0pt}{0}{k}{i}i!\lambda_i \leq C + \sum_{i=0}^ki^k4^i \leq C(4k)^k \leq k^{2k} \]
\[ \mu_k = \sum_{i=0}^k\genfrac\{\}{0pt}{0}{k}{i}i!\lambda_i \leq C + \sum_{i=0}^ki^k4^i \leq C(4k)^k \leq k^{2k} \]
for k large enough, showing that Carleman’s condition holds. Hence the sequence
![]() $(q_i)_{i\in\mathbb{N}}$
is indeed unique, and the proof is complete.
$(q_i)_{i\in\mathbb{N}}$
is indeed unique, and the proof is complete.
Lemma 9. For any
![]() $L \geq 1$
,
$L \geq 1$
,
![]() $n \geq 1$
, and
$n \geq 1$
, and
![]() $x \in \mathbb{R}$
,
$x \in \mathbb{R}$
,
 \[ \sum_{j=1}^L\sum_{\ell = 1}^j({-}1)^{\ell+j}\binom{L+n}{j+n}\binom{j-\ell + n - 1}{n-1}x^\ell = (1+x)^L - 1. \]
\[ \sum_{j=1}^L\sum_{\ell = 1}^j({-}1)^{\ell+j}\binom{L+n}{j+n}\binom{j-\ell + n - 1}{n-1}x^\ell = (1+x)^L - 1. \]
Proof. Changing the order of summation, it is enough to prove that, for
![]() $L\geq 1$
,
$L\geq 1$
,
![]() $n \geq 1$
, and
$n \geq 1$
, and
![]() $1 \leq \ell \leq L$
,
$1 \leq \ell \leq L$
,
 \begin{equation*} \sum_{j=\ell}^L({-}1)^{j+\ell}\binom{L+n}{j+n}\binom{j-\ell+n-1}{n-1} = \binom{L}{\ell}. \end{equation*}
\begin{equation*} \sum_{j=\ell}^L({-}1)^{j+\ell}\binom{L+n}{j+n}\binom{j-\ell+n-1}{n-1} = \binom{L}{\ell}. \end{equation*}
We prove this by induction on L. It holds for
![]() $L = 1$
, and assuming for
$L = 1$
, and assuming for
![]() $L \geq 1$
, for
$L \geq 1$
, for
![]() $L+1$
we have, by the induction hypothesis for
$L+1$
we have, by the induction hypothesis for
![]() $(L,\ell, n)$
and
$(L,\ell, n)$
and
![]() $(L, \ell-1, n)$
,
$(L, \ell-1, n)$
,
 \begin{align*} \sum_{j=\ell}^{L+1}({-}1)^{j+\ell} & \binom{L+1+n}{j+n}\binom{j-\ell+n-1}{n-1} \\ & = \binom{L}{\ell} + \sum_{j=\ell}^{L+1}({-}1)^{j+\ell}\binom{L+n}{j+n-1}\binom{j-\ell+n-1}{n-1} \\ & = \binom{L}{\ell} + \sum_{j=\ell-1}^{L}({-}1)^{j+\ell-1}\binom{L+n}{j+n}\binom{j-(\ell-1)+n-1}{n-1} \\ & = \binom{L}{\ell} + \binom{L}{\ell-1} = \binom{L+1}{\ell}, \end{align*}
\begin{align*} \sum_{j=\ell}^{L+1}({-}1)^{j+\ell} & \binom{L+1+n}{j+n}\binom{j-\ell+n-1}{n-1} \\ & = \binom{L}{\ell} + \sum_{j=\ell}^{L+1}({-}1)^{j+\ell}\binom{L+n}{j+n-1}\binom{j-\ell+n-1}{n-1} \\ & = \binom{L}{\ell} + \sum_{j=\ell-1}^{L}({-}1)^{j+\ell-1}\binom{L+n}{j+n}\binom{j-(\ell-1)+n-1}{n-1} \\ & = \binom{L}{\ell} + \binom{L}{\ell-1} = \binom{L+1}{\ell}, \end{align*}
as claimed.
Proof of Theorem 4. In order to handle assumptions (i) and (ii) together, under (i) we use the notation
![]() $\lambda_k = 0$
for
$\lambda_k = 0$
for
![]() $k \geq K$
. Then the limiting g.f.
$k \geq K$
. Then the limiting g.f.
![]() $f_Y$
is given in (3).
$f_Y$
is given in (3).
First, assume that
![]() $\nu > 0$
. Substituting the Taylor series of the logarithm,
$\nu > 0$
. Substituting the Taylor series of the logarithm,
into (3), expanding
![]() $(1-s)^i$
, and gathering together the powers of s, we have
$(1-s)^i$
, and gathering together the powers of s, we have
 \begin{align} f_Y(s) & = \exp\!\Bigg\{{-}\!\sum_{k=1}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\!\log\bigg(1+\frac{\nu}{2}\bigg) - \sum_{n=1}^\infty\frac{1}{n}\bigg(\frac{\nu}{2 + \nu}\bigg)^n s^n + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}\sum_{j=0}^i\binom{i}{j}({-}s)^j\Bigg)\Bigg\} \nonumber \\ & = \exp\Bigg\{{-}\sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1+\frac{\nu}{2}\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^{i}}{i2^{i}}\Bigg) \nonumber \\ & \qquad\qquad + \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=1}^\infty s^n \Bigg(n^{-1}\bigg(\frac{\nu}{2+\nu}\bigg)^{n} - \sum_{i=n}^{k-1}({-}1)^{i+n}\frac{\nu^i}{i 2^i}\binom{i}{n}\Bigg)\Bigg\}, \end{align}
\begin{align} f_Y(s) & = \exp\!\Bigg\{{-}\!\sum_{k=1}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\!\log\bigg(1+\frac{\nu}{2}\bigg) - \sum_{n=1}^\infty\frac{1}{n}\bigg(\frac{\nu}{2 + \nu}\bigg)^n s^n + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^i}{i2^i}\sum_{j=0}^i\binom{i}{j}({-}s)^j\Bigg)\Bigg\} \nonumber \\ & = \exp\Bigg\{{-}\sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k} \Bigg(\log\bigg(1+\frac{\nu}{2}\bigg) + \sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^{i}}{i2^{i}}\Bigg) \nonumber \\ & \qquad\qquad + \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=1}^\infty s^n \Bigg(n^{-1}\bigg(\frac{\nu}{2+\nu}\bigg)^{n} - \sum_{i=n}^{k-1}({-}1)^{i+n}\frac{\nu^i}{i 2^i}\binom{i}{n}\Bigg)\Bigg\}, \end{align}
where the empty sum is defined to be 0. We claim that the order of summation in (34) with respect to k and n can be interchanged. Indeed, this is clear under (i), since the sum in k is in fact finite.
Assume (ii). Then Taylor’s theorem applied to the function
![]() $(1+x)^{-n}$
with
$(1+x)^{-n}$
with
![]() $n \leq k -1$
gives
$n \leq k -1$
gives
 \[ (1 + x)^{-n} = n\sum_{\ell=n}^{k-1}({-}1)^{\ell+n}\binom{\ell}{n}\frac{x^{\ell-n}}{\ell} + ({-}1)^{k-n}\binom{k-1}{k-n}(1 + \xi)^{-k} x^{k-n}, \]
\[ (1 + x)^{-n} = n\sum_{\ell=n}^{k-1}({-}1)^{\ell+n}\binom{\ell}{n}\frac{x^{\ell-n}}{\ell} + ({-}1)^{k-n}\binom{k-1}{k-n}(1 + \xi)^{-k} x^{k-n}, \]
with
![]() $\xi \in (0,x)$
. Therefore,
$\xi \in (0,x)$
. Therefore,
 \begin{equation} \Bigg|\sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{x^{i-n}}{i} - n^{-1}(1 + x)^{-n}\Bigg| \leq n^{-1}\binom{k-1}{k-n}x^{k-n}, \end{equation}
\begin{equation} \Bigg|\sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{x^{i-n}}{i} - n^{-1}(1 + x)^{-n}\Bigg| \leq n^{-1}\binom{k-1}{k-n}x^{k-n}, \end{equation}
thus, with
![]() $x = \nu / 2$
,
$x = \nu / 2$
,
 \begin{align*} \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=1}^{k-1}s^n \Bigg|\sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{\nu^{i}}{2^i i} - n^{-1}\bigg(\frac{\nu}{2+\nu}\bigg)^{n}\Bigg| & \leq \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=1}^{k-1}s^n \frac{\nu^n}{2^n}n^{-1}\binom{k-1}{k-n}\frac{\nu^{k-n}}{2^{k-n}} \\ & = \sum_{k=1}^\infty\lambda_k\sum_{n=1}^{k-1}s^n n^{-1}\binom{k-1}{k-n} \\ & \leq \sum_{k=1}^\infty\lambda_k(1+s)^k, \end{align*}
\begin{align*} \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=1}^{k-1}s^n \Bigg|\sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{\nu^{i}}{2^i i} - n^{-1}\bigg(\frac{\nu}{2+\nu}\bigg)^{n}\Bigg| & \leq \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=1}^{k-1}s^n \frac{\nu^n}{2^n}n^{-1}\binom{k-1}{k-n}\frac{\nu^{k-n}}{2^{k-n}} \\ & = \sum_{k=1}^\infty\lambda_k\sum_{n=1}^{k-1}s^n n^{-1}\binom{k-1}{k-n} \\ & \leq \sum_{k=1}^\infty\lambda_k(1+s)^k, \end{align*}
which is finite for
![]() $s \in (0,1)$
if
$s \in (0,1)$
if
![]() $\limsup \lambda_n^{1/n} \leq \frac12$
. The other part is easy to handle, as
$\limsup \lambda_n^{1/n} \leq \frac12$
. The other part is easy to handle, as
 \[ \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=k}^\infty s^n n^{-1}\bigg(\frac{\nu}{2 + \nu}\bigg)^n \leq \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}s^k\bigg(\frac{\nu}{2 + \nu}\bigg)^k = \sum_{k=1}^\infty\frac{2^k\lambda_k}{(2 + \nu)^k}s^k, \]
\[ \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}\sum_{n=k}^\infty s^n n^{-1}\bigg(\frac{\nu}{2 + \nu}\bigg)^n \leq \sum_{k=1}^\infty\frac{2^k\lambda_k}{\nu^k}s^k\bigg(\frac{\nu}{2 + \nu}\bigg)^k = \sum_{k=1}^\infty\frac{2^k\lambda_k}{(2 + \nu)^k}s^k, \]
which is summable.
Summarizing, in both cases the order of summation in (34) can be interchanged, and doing so we obtain
![]() $f_Y(s) = \exp\big\{{-}A_0 + \sum_{n=1}^\infty A_n s^n\big\}$
, where
$f_Y(s) = \exp\big\{{-}A_0 + \sum_{n=1}^\infty A_n s^n\big\}$
, where
 \begin{equation} \begin{split} A_0 & = \sum_{k=1}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^{i}}{i2^{i}} + \log\bigg(1+\frac{\nu}{2}\bigg)\Bigg), \\ A_n & = \sum_{k=1}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\bigg(\frac{\nu}{2+\nu}\bigg)^n n^{-1} - \sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{\nu^{i}}{i2^{i}}\Bigg). \end{split} \end{equation}
\begin{equation} \begin{split} A_0 & = \sum_{k=1}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\sum_{i=1}^{k-1}({-}1)^{i}\frac{\nu^{i}}{i2^{i}} + \log\bigg(1+\frac{\nu}{2}\bigg)\Bigg), \\ A_n & = \sum_{k=1}^{\infty}\frac{2^k\lambda_k}{\nu^k} \Bigg(\bigg(\frac{\nu}{2+\nu}\bigg)^n n^{-1} - \sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{\nu^{i}}{i2^{i}}\Bigg). \end{split} \end{equation}
Recall the notation from the proof of Lemma 8. By (30), using the inversion formula for Stirling numbers of the first and second kind (see, e.g., [Reference Graham, Knuth and Patashnik10, Exercise 12, p. 310]), we have
 \[ k! \lambda_k = \sum_{i=0}^k ({-}1)^{k+i} \genfrac[]{0pt}{0}{k}{i} \mu_k, \]
\[ k! \lambda_k = \sum_{i=0}^k ({-}1)^{k+i} \genfrac[]{0pt}{0}{k}{i} \mu_k, \]
where![]() represents the Stirling number of the first kind. Substituting (33), and using
represents the Stirling number of the first kind. Substituting (33), and using
 \[ \sum_{i=0}^k ({-}1)^{k+i} \genfrac[]{0pt}{0}{k}{i} j^k = j (j-1) \cdots (j-k+1) \]
\[ \sum_{i=0}^k ({-}1)^{k+i} \genfrac[]{0pt}{0}{k}{i} j^k = j (j-1) \cdots (j-k+1) \]
(see, e.g., [Reference Graham, Knuth and Patashnik10, p. 263, (6.13)]), we obtain the formula
 \begin{equation} \lambda_k = \sum_{j=k}^\infty \binom{j}{k} q_j. \end{equation}
\begin{equation} \lambda_k = \sum_{j=k}^\infty \binom{j}{k} q_j. \end{equation}
We also see that
![]() $\lambda_k = 0$
implies
$\lambda_k = 0$
implies
![]() $q_j = 0$
for all
$q_j = 0$
for all
![]() $j \geq k$
. Substituting (37) back into (36) we claim that the order of summation with respect to k and j can be interchanged. This is again clear under (i), while under (ii), by (35),
$j \geq k$
. Substituting (37) back into (36) we claim that the order of summation with respect to k and j can be interchanged. This is again clear under (i), while under (ii), by (35),
 \begin{align*} \sum_{k=n+1}^\infty\sum_{j=k}^\infty\frac{2^k}{\nu^k}q_j\binom{j}{k}\Bigg|\sum_{i=n}^{k-1}({-}1)^{i+n} & \binom{i}{n} \frac{\nu^i}{i 2^i}- n^{-1} \frac{\nu^n}{(2+\nu)^n} \Bigg| \\ & \leq \sum_{k=n+1}^\infty\sum_{j=k}^\infty\frac{2^k}{\nu^k}q_j\binom{j}{k}\frac{\nu^n}{2^n}n^{-1} \binom{k-1}{k-n}\frac{\nu^{k-n}}{2^{k-n}} \\ & = \sum_{k=n+1}^\infty\lambda_k n^{-1}\binom{k-1}{k-n} < \infty, \end{align*}
\begin{align*} \sum_{k=n+1}^\infty\sum_{j=k}^\infty\frac{2^k}{\nu^k}q_j\binom{j}{k}\Bigg|\sum_{i=n}^{k-1}({-}1)^{i+n} & \binom{i}{n} \frac{\nu^i}{i 2^i}- n^{-1} \frac{\nu^n}{(2+\nu)^n} \Bigg| \\ & \leq \sum_{k=n+1}^\infty\sum_{j=k}^\infty\frac{2^k}{\nu^k}q_j\binom{j}{k}\frac{\nu^n}{2^n}n^{-1} \binom{k-1}{k-n}\frac{\nu^{k-n}}{2^{k-n}} \\ & = \sum_{k=n+1}^\infty\lambda_k n^{-1}\binom{k-1}{k-n} < \infty, \end{align*}
since
Thus, the order of summation is indeed interchangeable, and we obtain
 \begin{align} A_n & = \sum_{j=1}^\infty q_j\Bigg\{\bigg[\bigg(1 + \frac{2}{\nu}\bigg)^j - 1\bigg] \bigg(\frac{\nu}{2 + \nu}\bigg)^n n^{-1} - \sum_{k=n+1}^j\frac{2^k}{\nu^k}\binom{j}{k}\sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{\nu^i}{i 2^i}\Bigg\} \nonumber \\ & \;=\!:\; \sum_{j=1}^\infty q_j B(n,j). \end{align}
\begin{align} A_n & = \sum_{j=1}^\infty q_j\Bigg\{\bigg[\bigg(1 + \frac{2}{\nu}\bigg)^j - 1\bigg] \bigg(\frac{\nu}{2 + \nu}\bigg)^n n^{-1} - \sum_{k=n+1}^j\frac{2^k}{\nu^k}\binom{j}{k}\sum_{i=n}^{k-1}({-}1)^{i+n}\binom{i}{n}\frac{\nu^i}{i 2^i}\Bigg\} \nonumber \\ & \;=\!:\; \sum_{j=1}^\infty q_j B(n,j). \end{align}
We claim that
This is clear for
![]() $j \leq n$
. Writing
$j \leq n$
. Writing
![]() $\ell = k -i$
in the summation and using Lemma 9 with
$\ell = k -i$
in the summation and using Lemma 9 with
![]() $L = j-n$
we obtain
$L = j-n$
we obtain
 \begin{align*} \sum_{k=n+1}^j\sum_{i=n}^{k-1}({-}1)^i\binom{j}{k}\binom{i-1}{n-1}x^{k-i} & = \sum_{k=n+1}^j\sum_{\ell=1}^{k-n}({-}1)^{k+\ell}\binom{j}{k}\binom{k-\ell-1}{n-1}x^\ell \\ & = ({-}1)^n[(1+x)^{j-n}-1]. \end{align*}
\begin{align*} \sum_{k=n+1}^j\sum_{i=n}^{k-1}({-}1)^i\binom{j}{k}\binom{i-1}{n-1}x^{k-i} & = \sum_{k=n+1}^j\sum_{\ell=1}^{k-n}({-}1)^{k+\ell}\binom{j}{k}\binom{k-\ell-1}{n-1}x^\ell \\ & = ({-}1)^n[(1+x)^{j-n}-1]. \end{align*}
Using that
![]() $n \binom{i}{n} = i \binom{i-1}{n-1}$
, and substituting back into (38) with
$n \binom{i}{n} = i \binom{i-1}{n-1}$
, and substituting back into (38) with
![]() $x= 2/\nu$
, we have
$x= 2/\nu$
, we have
which after simplification gives (39).
Now let
![]() $\nu = 0$
. In this case the calculations are again simpler. Expanding
$\nu = 0$
. In this case the calculations are again simpler. Expanding
![]() $(s-1)^i$
and changing the order of summation,
$(s-1)^i$
and changing the order of summation,
Substituting (37) and changing the order of summation again we get
 \begin{equation} A_n = \sum_{j=n}^\infty q_j\sum_{k=n}^j\binom{k}{n}\binom{j}{k}({-}1)^{k+n}\frac{1}{k}. \end{equation}
\begin{equation} A_n = \sum_{j=n}^\infty q_j\sum_{k=n}^j\binom{k}{n}\binom{j}{k}({-}1)^{k+n}\frac{1}{k}. \end{equation}
The changes of the order of summation can be justified as in the previous case. For the coefficient of
![]() $q_j$
we have
$q_j$
we have
 \[ \sum_{k=n}^j\binom{k}{n}\binom{j}{k}({-}1)^{k+n}\frac{1}{k} = \binom{j}{n}\sum_{k=n}^j\frac{1}{k}\binom{j-n}{k-n}({-}1)^{k+n} = \frac{1}{n}, \]
\[ \sum_{k=n}^j\binom{k}{n}\binom{j}{k}({-}1)^{k+n}\frac{1}{k} = \binom{j}{n}\sum_{k=n}^j\frac{1}{k}\binom{j-n}{k-n}({-}1)^{k+n} = \frac{1}{n}, \]
where we used that for
![]() $j \geq n$
,
$j \geq n$
,
 \[ \sum_{k=0}^{j-n}({-}1)^k\frac{j}{k+n}\binom{j-n}{k} = \binom{j-1}{n-1}^{-1}. \]
\[ \sum_{k=0}^{j-n}({-}1)^k\frac{j}{k+n}\binom{j-n}{k} = \binom{j-1}{n-1}^{-1}. \]
The latter formula follows by induction on j. Substituting back into (40), the proof is complete.
Acknowledgement
We are grateful to Mátyás Barczy for discussions on the topic. We thank the anonymous referees for useful comments and remarks, and in particular for suggesting allowing supercritical generations, which led to more general results.
Funding information
This research was supported by the Ministry of Culture and Innovation of Hungary from the National Research, Development and Innovation Fund, project no. TKP2021-NVA-09. Kevei’s research was partially supported by the János Bolyai Research Scholarship of the Hungarian Academy of Sciences.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.