Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T17:53:34.660Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounding the stochastic performance of continuum structure functions. II

Published online by Cambridge University Press:  14 July 2016

Laurence A. Baxter  and
Chul Kim
Laurence A. Baxter*
Affiliation:
State University of New York at Stony Brook
Chul Kim
Affiliation:
State University of New York at Stony Brook
*
∗Postal address: Department of Applied Mathematics and Statistics, State University of New York at Stony Brook, Stony Brook, NY 11794, USA.
Get access Rights & Permissions [Opens in a new window]

Abstract

A continuum structure function γ is a non-decreasing mapping from the unit hypercube to the unit interval. Block and Savits (1984) use the sets 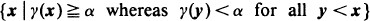and 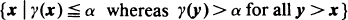to determine bounds on the distribution of γ (X) when X is a vector of associated random variables. It is shown that, if γ admits of a modular decomposition, improved bounds may be obtained.

Keywords

MODULAR DECOMPOSITIONASSOCIATED RANDOM VARIABLE
Type
Research Papers
Information
Journal of Applied Probability , Volume 24 , Issue 3 , September 1987 , pp. 609 - 618
Copyright
Copyright © Applied Probability Trust 1987 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

∗∗

Present address: Agency for Defense Development, P.O. Box 35, Daejeon, Korea.

Research supported by the National Science Foundation under grant ECS-8306871 and by the Air Force Office of Scientific Research, AFSC, USAF, under grant AFOSR-84-0243. The US Government is authorised to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright notation thereon.

References

Barlow, R. E. and Proschan, F. (1975) Statistical Theory of Reliability and Life Testing. Holt, Rinehart and Winston, New York.Google Scholar
Baxter, L. A. (1984) Continuum structures I. J. Appl. Prob. 21, 802–815.CrossRefGoogle Scholar
Baxter, L. A. (1986) Continuum structures II. Math. Proc. Camb. Phil. Soc. 99, 331–338.Google Scholar
Baxter, L. A. and Kim, C. (1986) Bounding the stochastic performance of continuum structure functions I. J. Appl. Prob. 23, 660–669.CrossRefGoogle Scholar
Block, H. W. and Savits, T. H. (1984) Continuous multistate structure functions. Operat. Res. 32, 703–714.Google Scholar
Butler, D. (1982) Bounding the reliability of multistate systems. Operat. Res. 30, 530–544.CrossRefGoogle Scholar
Funnemark, E. and Natvig, B. (1985) Bounds for the availabilities in a fixed time interval for multistate monotone systems. Adv. Appl. Prob. 17, 638–665.CrossRefGoogle Scholar
Royden, H. L. (1968) Real Analysis, 2nd edn. Macmillan, New York.Google Scholar