1. Introduction
Let
![]() $U\;:\!= (U_t)_{t \geq 0} $
be a one-dimensional Ornstein–Uhlenbeck (OU for short) process defined on a filtered probability space
$U\;:\!= (U_t)_{t \geq 0} $
be a one-dimensional Ornstein–Uhlenbeck (OU for short) process defined on a filtered probability space
![]() $(\Omega, (\mathcal{F})_{t \geq 0}, \mathcal{F}, \mathbb{P})$
as the unique solution to the following stochastic differential equation (SDE):
$(\Omega, (\mathcal{F})_{t \geq 0}, \mathcal{F}, \mathbb{P})$
as the unique solution to the following stochastic differential equation (SDE):
where
![]() $(B_t)_{t \geq 0}$
is a standard Brownian motion (BM) starting at 0 and
$(B_t)_{t \geq 0}$
is a standard Brownian motion (BM) starting at 0 and
![]() $k \in \mathbb{R}$
is a constant. The OU process is a Gauss–Markov process with transition density function given by
$k \in \mathbb{R}$
is a constant. The OU process is a Gauss–Markov process with transition density function given by
where
![]() $\phi(z)= {\mathrm{e}}^{-{{z^2}/{2}}}/\sqrt{2 \pi}$
,
$\phi(z)= {\mathrm{e}}^{-{{z^2}/{2}}}/\sqrt{2 \pi}$
,
![]() $z \in \mathbb{R}$
, is the probability density function of the standard normal distribution and
$z \in \mathbb{R}$
, is the probability density function of the standard normal distribution and
where
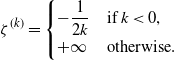 \begin{align*} \zeta^{(k)} = \begin{cases}- \dfrac{1}{2k} & \text{if $ k < 0$,}\\+\infty & \text{otherwise.}\end{cases}\end{align*}
\begin{align*} \zeta^{(k)} = \begin{cases}- \dfrac{1}{2k} & \text{if $ k < 0$,}\\+\infty & \text{otherwise.}\end{cases}\end{align*}
It is well known by the Dambis–Dubins–Schwarz theorem (see e.g. [Reference Revuz and Yor32, Theorem V.1.6]) that the OU process can be written in terms of a time-changed BM
![]() $(W_t)_{t \geq 0}$
as
$(W_t)_{t \geq 0}$
as
Let
![]() $f \in \mathcal{C}([0,\infty), \mathbb{R})$
be such that
$f \in \mathcal{C}([0,\infty), \mathbb{R})$
be such that
![]() $f(0) \neq 0$
, with
$f(0) \neq 0$
, with
![]() $\mathcal{C}(I, K)$
denoting the space of continuous functions from I into K for some intervals I and
$\mathcal{C}(I, K)$
denoting the space of continuous functions from I into K for some intervals I and
![]() $K \subseteq \mathbb{R}$
. We are interested in the first passage time (FPT) of the OU to f given by
$K \subseteq \mathbb{R}$
. We are interested in the first passage time (FPT) of the OU to f given by
with
![]() $\inf\{ \emptyset \} = \infty$
. The main goal of this paper is to derive, via different methods, an explicit analytical expression linking the distribution of
$\inf\{ \emptyset \} = \infty$
. The main goal of this paper is to derive, via different methods, an explicit analytical expression linking the distribution of
![]() $T_{k}^f$
to that of
$T_{k}^f$
to that of
![]() $T_{k}^{S^{\alpha,\beta}_k f}$
. Here, the two-parameter family of curves
$T_{k}^{S^{\alpha,\beta}_k f}$
. Here, the two-parameter family of curves
![]() $\bigl\{ S^{\alpha,\beta}_kf ;\, \alpha \neq 0, \beta \in \mathbb{R} \bigr\}$
is defined by
$\bigl\{ S^{\alpha,\beta}_kf ;\, \alpha \neq 0, \beta \in \mathbb{R} \bigr\}$
is defined by
where
 \begin{align*} \zeta_{k,\alpha, \beta} = \begin{cases}s\biggl({-} \dfrac{1}{\alpha \beta}\biggr) & \text{if $\alpha \beta <0$, $k \geq 0$,}\\s\biggl({-} \dfrac{1}{\alpha \beta + 2 k \alpha^2 }\biggr) &\text{if}\; 0<\dfrac{2k}{\alpha \beta + 2k \alpha^2}<1,\; k<0,\\ + \infty & \text{otherwise.}\end{cases}\end{align*}
\begin{align*} \zeta_{k,\alpha, \beta} = \begin{cases}s\biggl({-} \dfrac{1}{\alpha \beta}\biggr) & \text{if $\alpha \beta <0$, $k \geq 0$,}\\s\biggl({-} \dfrac{1}{\alpha \beta + 2 k \alpha^2 }\biggr) &\text{if}\; 0<\dfrac{2k}{\alpha \beta + 2k \alpha^2}<1,\; k<0,\\ + \infty & \text{otherwise.}\end{cases}\end{align*}
By doing so, we generalise the results obtained for a BM in [Reference Alili and Patie2], which can be immediately recovered from ours by letting
![]() $k\to 0$
, i.e.
$k\to 0$
, i.e.
![]() $T^f_0, S^{\alpha,\beta}_0$
, and
$T^f_0, S^{\alpha,\beta}_0$
, and
![]() $\zeta_{0,\alpha,\beta}$
. To simplify the notation and for consistency with [Reference Alili and Patie2], we drop the subscript 0 when referring to the BM.
$\zeta_{0,\alpha,\beta}$
. To simplify the notation and for consistency with [Reference Alili and Patie2], we drop the subscript 0 when referring to the BM.
To the best of our knowledge, explicit results for the FPT of the OU to f only exist for constants [Reference Alili, Patie and Pedersen3, Reference Ricciardi, Sacerdote and Sato34] or hyperbolic-type boundaries [Reference Buonocore, Nobile and Ricciardi13, Reference Daniels14]. Further results for the boundary crossing problem of Gauss–Markov processes to moving boundaries have been obtained in, for example, [Reference Buonocore, Caputo, Nobile and Pirozzi12], [Reference D’Onofrio and Pirozzi16], [Reference Durbin17], and [Reference Pirozzi30]. We also refer to [Reference Bluman7] and [Reference Sacerdote37] for applications of Lie symmetries to FPT problems. Our main result, stated in Theorem 3.1, allows us to map those results for the law of the FPT of
![]() $T_{k}^f$
to that of
$T_{k}^f$
to that of
![]() $T_{k}^{S^{\alpha,\beta}_k f} $
for the OU process. Such problems are of great interest, as the OU process has been used in many applications to model objects such as interest rates in finance or the evolution of the neuronal membrane voltages in neuroscience; see e.g. [Reference Alili, Patie and Pedersen3] and citations therein. The results for the process
$T_{k}^{S^{\alpha,\beta}_k f} $
for the OU process. Such problems are of great interest, as the OU process has been used in many applications to model objects such as interest rates in finance or the evolution of the neuronal membrane voltages in neuroscience; see e.g. [Reference Alili, Patie and Pedersen3] and citations therein. The results for the process
![]() $U^\mu\;:\!= (U_t^\mu)_{t\geq 0}$
defined for each
$U^\mu\;:\!= (U_t^\mu)_{t\geq 0}$
defined for each
![]() $t>0$
by
$t>0$
by
![]() $U_t^\mu\;:\!= U_t+\mu(1-{\mathrm{e}}^{-kt})$
, known as an OU process with drift
$U_t^\mu\;:\!= U_t+\mu(1-{\mathrm{e}}^{-kt})$
, known as an OU process with drift
![]() $\mu$
(see [Reference Alili, Patie and Pedersen3, Remark 2.5]), can be directly obtained from our results (for an OU without drift) after some transformations, as discussed in Remark 3.1.
$\mu$
(see [Reference Alili, Patie and Pedersen3, Remark 2.5]), can be directly obtained from our results (for an OU without drift) after some transformations, as discussed in Remark 3.1.
The paper is organised as follows. In Section 2.1 we introduce some notation and provide the key results for the
![]() $S^{\alpha,\beta}$
operator for the BM. The OU functional setting is presented in Section 2.2. In Section 2.3 we recall the different constructions of OU bridges and their properties. In particular, the process
$S^{\alpha,\beta}$
operator for the BM. The OU functional setting is presented in Section 2.2. In Section 2.3 we recall the different constructions of OU bridges and their properties. In particular, the process
![]() $\bigl({S}_k^{1,-1/r(T)}U_t, 0< t \leq T \bigr)$
has the same law as an OU bridge of length T from 0 to 0, for some
$\bigl({S}_k^{1,-1/r(T)}U_t, 0< t \leq T \bigr)$
has the same law as an OU bridge of length T from 0 to 0, for some
![]() $T>0$
. Section 3 is devoted to the statement of Theorem 3.1, which contains the main result of the paper, and two examples of its application. In Section 4 we discuss the properties of the
$T>0$
. Section 3 is devoted to the statement of Theorem 3.1, which contains the main result of the paper, and two examples of its application. In Section 4 we discuss the properties of the
![]() ${S}^{\alpha,\beta}_kf$
transformation with its connection to a certain nonlinear differential equation (Lemma 4.1), while in Section 5 we prove Theorem 3.1 in three different ways. In the first proof we use the relationship between the FPT of an OU and that of a BM. In the second proof we use a generalisation of the Gauss–Markov processes introduced in [Reference Alili and Patie2, Section 3.2] and find an analogue version of that proof in our case. In the third proof we use the Lie algebra to find the symmetries of the Fokker–Planck equation or the Kolmogorov forward differential equation
${S}^{\alpha,\beta}_kf$
transformation with its connection to a certain nonlinear differential equation (Lemma 4.1), while in Section 5 we prove Theorem 3.1 in three different ways. In the first proof we use the relationship between the FPT of an OU and that of a BM. In the second proof we use a generalisation of the Gauss–Markov processes introduced in [Reference Alili and Patie2, Section 3.2] and find an analogue version of that proof in our case. In the third proof we use the Lie algebra to find the symmetries of the Fokker–Planck equation or the Kolmogorov forward differential equation
Then, in Section 5.3, we use these symmetries to construct the function
![]() $h^{\alpha,\beta}_k$
of equation (5.8), derive our transformation
$h^{\alpha,\beta}_k$
of equation (5.8), derive our transformation
![]() $S^{\alpha,\beta}_kf$
and relate the FPT distribution of
$S^{\alpha,\beta}_kf$
and relate the FPT distribution of
![]() $T_{k}^f$
to that of
$T_{k}^f$
to that of
![]() $ T_{k}^{S^{\alpha,\beta}f}$
. In Section 6 we discuss the asymptotic distribution of
$ T_{k}^{S^{\alpha,\beta}f}$
. In Section 6 we discuss the asymptotic distribution of
![]() $T_{k}^{S^{\alpha, \beta}_kf}$
and the transience of the transformed curves
$T_{k}^{S^{\alpha, \beta}_kf}$
and the transience of the transformed curves
![]() $S^{\alpha,\beta}_kf$
. We provide the analogue of the Kolmogorov–Erdős–Petrovski transience test [Reference Erdős18] in the OU case and show its connection to the asymptotic behaviour of the FPT. Lastly, in Section 7, we use the method of images to obtain new classes of boundaries yielding explicit FPT distributions and use our
$S^{\alpha,\beta}_kf$
. We provide the analogue of the Kolmogorov–Erdős–Petrovski transience test [Reference Erdős18] in the OU case and show its connection to the asymptotic behaviour of the FPT. Lastly, in Section 7, we use the method of images to obtain new classes of boundaries yielding explicit FPT distributions and use our
![]() ${S}^{\alpha,\beta}_kf$
transformation (1.2) to produce new examples. A limitation of this method is that it only works for boundaries with certain properties given in Lemma 7.1.
${S}^{\alpha,\beta}_kf$
transformation (1.2) to produce new examples. A limitation of this method is that it only works for boundaries with certain properties given in Lemma 7.1.
As the authors were finalising the paper, they discovered that the
![]() $S^{\alpha,\beta}_k$
transformation, a variant of the boundary crossing identity (3.1) in Theorem 3.1 and the Lie symmetries (5.9), had previously appeared in [Reference Muravey27] (our (1.2) can be obtained by setting
$S^{\alpha,\beta}_k$
transformation, a variant of the boundary crossing identity (3.1) in Theorem 3.1 and the Lie symmetries (5.9), had previously appeared in [Reference Muravey27] (our (1.2) can be obtained by setting
![]() $A=k^2$
and
$A=k^2$
and
![]() $B=0$
in equation (39) therein), using the Lie approach. When comparing the results, they found misprints in one of their Lie symmetries and boundary crossing identity, as discussed in Section 5.3.
$B=0$
in equation (39) therein), using the Lie approach. When comparing the results, they found misprints in one of their Lie symmetries and boundary crossing identity, as discussed in Section 5.3.
2. Notation and preliminaries
We first introduce some functional spaces, transformations, and related results for the BM, as in [Reference Alili and Patie2], in Section 2.1, and then define the corresponding functional objects for the OU in Section 2.2. We end this section by providing different representations of OU bridges and highlighting their connection to our functional transformations.
2.1. Brownian motion setting
We start by introducing a nonlinear operator
![]() $\tau$
defined on the space of functions whose reciprocals are square-integrable in some (possibly infinite) interval of
$\tau$
defined on the space of functions whose reciprocals are square-integrable in some (possibly infinite) interval of
![]() $\mathbb{R}^+=[0,\infty)$
by
$\mathbb{R}^+=[0,\infty)$
by
and use it to define
where
![]() $a,b\in\mathbb{R}^+$
. In [Reference Alili and Patie2], the authors derived the following relationship between the laws of the FPTs of
$a,b\in\mathbb{R}^+$
. In [Reference Alili and Patie2], the authors derived the following relationship between the laws of the FPTs of
![]() $T^f$
and
$T^f$
and
![]() $T^{S^{\alpha,\beta} f}$
,
$T^{S^{\alpha,\beta} f}$
,
for
![]() $t<\zeta_{0, \alpha, \beta}$
, where
$t<\zeta_{0, \alpha, \beta}$
, where
![]() $S^{\alpha,\beta}$
is the two-parameter family of transformations
$S^{\alpha,\beta}$
is the two-parameter family of transformations
![]() $S^{\alpha,\beta}\colon A_{\infty}\to A_{\infty}$
given by
$S^{\alpha,\beta}\colon A_{\infty}\to A_{\infty}$
given by
Equation (2.1) extends a previous result by the same authors for a relationship between the laws of the FPT of
![]() $T^f$
and
$T^f$
and
![]() $T^{S^{1,\beta} f}$
, with the one-parameter family of transformations
$T^{S^{1,\beta} f}$
, with the one-parameter family of transformations
![]() $\{S^{1,\beta} f, \beta \in \mathbb{R}\}$
obtained using the construction of Brownian bridges; see [Reference Alili and Patie1]. The connection to Brownian bridges naturally appears as
$\{S^{1,\beta} f, \beta \in \mathbb{R}\}$
obtained using the construction of Brownian bridges; see [Reference Alili and Patie1]. The connection to Brownian bridges naturally appears as
![]() $(S^{1,-1/T}(B)_t , 0 \leq t < T )$
is a Brownian bridge of length T from 0 to 0; see [Reference Borodin and Salminen10, page 64]. Besides deriving (2.1) in [Reference Alili and Patie2], the authors also showed that the transformation
$(S^{1,-1/T}(B)_t , 0 \leq t < T )$
is a Brownian bridge of length T from 0 to 0; see [Reference Borodin and Salminen10, page 64]. Besides deriving (2.1) in [Reference Alili and Patie2], the authors also showed that the transformation
![]() $S^{\alpha,\beta}$
can be obtained as
$S^{\alpha,\beta}$
can be obtained as
where
![]() $\circ$
denotes the composition operator. Here
$\circ$
denotes the composition operator. Here
![]() $\Sigma\colon A_{\infty} \to A_{\infty}$
is the involution operator, i.e.
$\Sigma\colon A_{\infty} \to A_{\infty}$
is the involution operator, i.e.
![]() $\Sigma \circ \Sigma = \mathrm{Id}$
, specified by
$\Sigma \circ \Sigma = \mathrm{Id}$
, specified by
where
![]() $\rho$
is the inversion operator acting on the space of continuous monotone functions, i.e.
$\rho$
is the inversion operator acting on the space of continuous monotone functions, i.e.
![]() $ \rho f \circ f(t) = t$
. For
$ \rho f \circ f(t) = t$
. For
![]() $\alpha \in \mathbb{R}^*=\mathbb{R}\backslash\{0\}$
,
$\alpha \in \mathbb{R}^*=\mathbb{R}\backslash\{0\}$
,
![]() $\beta \in \mathbb{R}$
,
$\beta \in \mathbb{R}$
,
![]() $\Pi^{\alpha,\beta}\colon A_{\infty}\to A_{\infty}$
is the family of nonlinear operators given by
$\Pi^{\alpha,\beta}\colon A_{\infty}\to A_{\infty}$
is the family of nonlinear operators given by
As explained at the beginning of Section 2 of [Reference Alili and Patie2] and Appendix 8 of [Reference Revuz and Yor32], the operators (2.4) are closely related to the Sturm–Liouville equation
where
![]() $\mu$
denotes a positive Radon measure on
$\mu$
denotes a positive Radon measure on
![]() $\mathbb{R}^+$
and
$\mathbb{R}^+$
and
![]() $\phi^{\prime\prime}$
is the second derivative in the sense of distributions. In fact, if
$\phi^{\prime\prime}$
is the second derivative in the sense of distributions. In fact, if
![]() $\phi$
solves (2.5), then the vectorial space
$\phi$
solves (2.5), then the vectorial space
![]() $\{\Pi^{\alpha,\beta} \phi ;\, \alpha\neq 0, \beta \in \mathbb{R}\}$
is the set of other solutions to the same equation. Moreover, all positive solutions are convex and described by the set
$\{\Pi^{\alpha,\beta} \phi ;\, \alpha\neq 0, \beta \in \mathbb{R}\}$
is the set of other solutions to the same equation. Moreover, all positive solutions are convex and described by the set
![]() $\{\Pi^{\alpha,\beta} \varphi ;\, \alpha>0, \beta \geq 0\}$
, where
$\{\Pi^{\alpha,\beta} \varphi ;\, \alpha>0, \beta \geq 0\}$
, where
![]() $\varphi$
is the unique, positive, decreasing solution such that
$\varphi$
is the unique, positive, decreasing solution such that
![]() $\varphi(0)=1$
.
$\varphi(0)=1$
.
Moreover, it was noted in [Reference Alili and Patie2] that
![]() $S^{\alpha, \beta} \circ S^{\alpha^{\prime}, \beta^{\prime}} = S^{\alpha \alpha^{\prime}, \alpha \beta^{\prime} + {{\beta}/{\alpha^{\prime}}}}$
, for all couples
$S^{\alpha, \beta} \circ S^{\alpha^{\prime}, \beta^{\prime}} = S^{\alpha \alpha^{\prime}, \alpha \beta^{\prime} + {{\beta}/{\alpha^{\prime}}}}$
, for all couples
![]() $(\alpha, \beta)$
and
$(\alpha, \beta)$
and
![]() $(\alpha^{\prime}, \beta^{\prime}) \in \mathbb{R}^{*} \times \mathbb{R}$
, and that
$(\alpha^{\prime}, \beta^{\prime}) \in \mathbb{R}^{*} \times \mathbb{R}$
, and that
![]() $(S^{1, \beta})_{\beta \geq 0}$
is a semi-group, while
$(S^{1, \beta})_{\beta \geq 0}$
is a semi-group, while
![]() $(S^{1, \beta})_{\beta \in \mathbb{R}}$
and
$(S^{1, \beta})_{\beta \in \mathbb{R}}$
and
![]() $(S^{{{\mathrm{e}}^\alpha}, 0})_{\alpha \in \mathbb{R}}$
are groups.
$(S^{{{\mathrm{e}}^\alpha}, 0})_{\alpha \in \mathbb{R}}$
are groups.
2.2. Ornstein–Uhlenbeck setting
We shall now define the operators of interest on the space of functions
where
![]() $a,b \in \mathbb{R}^+$
, and
$a,b \in \mathbb{R}^+$
, and
with
![]() $\textrm{sgn}(k)$
being the sign of k and
$\textrm{sgn}(k)$
being the sign of k and
![]() $\mathbb{1}_A$
denoting the indicator function of the set A. Note that
$\mathbb{1}_A$
denoting the indicator function of the set A. Note that
![]() $A_{k,\infty}$
is the set of continuous functions that are of constant sign on some non-empty interval
$A_{k,\infty}$
is the set of continuous functions that are of constant sign on some non-empty interval
![]() $[0, l], \; l>0$
. Let the isomorphic nonlinear operators
$[0, l], \; l>0$
. Let the isomorphic nonlinear operators
![]() $\Lambda_k$
and
$\Lambda_k$
and
![]() $\Sigma_k$
be defined, on
$\Sigma_k$
be defined, on
![]() $A_{k,\infty}$
, by
$A_{k,\infty}$
, by
and
respectively. Note that the inverse of
![]() $\Lambda_k$
is
$\Lambda_k$
is
![]() $\Lambda_k^{-1}f(t)= {\mathrm{e}}^{-kt} f(r(t))$
. Here
$\Lambda_k^{-1}f(t)= {\mathrm{e}}^{-kt} f(r(t))$
. Here
![]() $\Lambda_k$
maps the curves from the OU setting to the corresponding curves in the BM setting, with limits
$\Lambda_k$
maps the curves from the OU setting to the corresponding curves in the BM setting, with limits
![]() $\lim_{k \to 0}\Lambda_k = \mathrm{Id}$
and
$\lim_{k \to 0}\Lambda_k = \mathrm{Id}$
and
![]() $\lim_{k\to 0} \Sigma_k = \Sigma$
. From (2.8) we can immediately see that
$\lim_{k\to 0} \Sigma_k = \Sigma$
. From (2.8) we can immediately see that
![]() $\Sigma_k$
can also be represented as
$\Sigma_k$
can also be represented as
Inspired by (2.3) in the BM setting, for
![]() $\alpha \in \mathbb{R}^*$
and
$\alpha \in \mathbb{R}^*$
and
![]() $\beta \in \mathbb{R}$
, define
$\beta \in \mathbb{R}$
, define
![]() ${S}_k^{\alpha, \beta}\colon A_{k,\infty}\to A_{k,\infty}$
by
${S}_k^{\alpha, \beta}\colon A_{k,\infty}\to A_{k,\infty}$
by
Alternatively,
![]() $S^{\alpha, \beta}_k$
can also be obtained as
$S^{\alpha, \beta}_k$
can also be obtained as
![]() $\Lambda_k^{-1}\circ S^{\alpha,\beta}\circ \Lambda_k$
, as shown in the proof of Lemma 4.1. This result provides us with an intuitive interpretation of this family of transformations. First we map the boundary f for the OU process to its corresponding boundary for the standard BM using the
$\Lambda_k^{-1}\circ S^{\alpha,\beta}\circ \Lambda_k$
, as shown in the proof of Lemma 4.1. This result provides us with an intuitive interpretation of this family of transformations. First we map the boundary f for the OU process to its corresponding boundary for the standard BM using the
![]() $\Lambda_{k}$
transformation. Then we use
$\Lambda_{k}$
transformation. Then we use
![]() $S^{\alpha,\beta}$
on this curve for the standard BM, and finally we revert it back to the OU problem via
$S^{\alpha,\beta}$
on this curve for the standard BM, and finally we revert it back to the OU problem via
![]() $\Lambda^{-1}_k$
, as illustrated in Figure 1.
$\Lambda^{-1}_k$
, as illustrated in Figure 1.
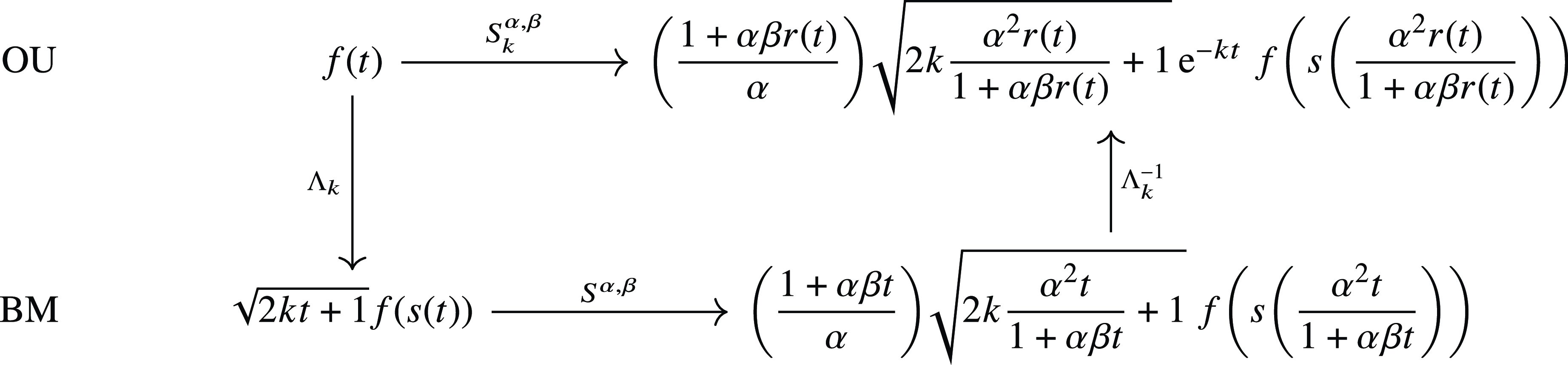
Figure 1. Flow chart of
![]() $S^{\alpha,\beta}_k$
.
$S^{\alpha,\beta}_k$
.
2.3. Ornstein–Uhlenbeck bridges
As mentioned in the Introduction,
![]() $S^{\alpha,\beta}_k$
for specific values of
$S^{\alpha,\beta}_k$
for specific values of
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
relates to a representation of the standard OU bridge. We shall now define this process and then recall its different representations, using the detailed analysis of both Wiener and OU bridges provided in [Reference Barczy and Kern5] and [Reference Borodin and Salminen10].
$\beta$
relates to a representation of the standard OU bridge. We shall now define this process and then recall its different representations, using the detailed analysis of both Wiener and OU bridges provided in [Reference Barczy and Kern5] and [Reference Borodin and Salminen10].
Definition 2.1. An OU bridge
![]() $U^{\mathrm{br}} = \{U^{\mathrm{br}}_{t}, t \in [0,T] \}$
from a to b, of length T, is characterised by the following properties:
$U^{\mathrm{br}} = \{U^{\mathrm{br}}_{t}, t \in [0,T] \}$
from a to b, of length T, is characterised by the following properties:
-
(i)
 $U^{\mathrm{br}}_{0}=a$
and
$U^{\mathrm{br}}_{0}=a$
and
 $U^{\mathrm{br}}_{T}=b$
(each with probability 1);
$U^{\mathrm{br}}_{T}=b$
(each with probability 1); -
(ii)
 $U^{\mathrm{br}}$
is a Gaussian process;
$U^{\mathrm{br}}$
is a Gaussian process; -
(iii)
 $\mathbb{E}[U^{\mathrm{br}}_{t}] = a \dfrac{\sinh{(k(T-t))}}{\sinh{(kt)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}}$
;
$\mathbb{E}[U^{\mathrm{br}}_{t}] = a \dfrac{\sinh{(k(T-t))}}{\sinh{(kt)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}}$
; -
(iv)
 $\text{Cov}(U^{\mathrm{br}}_{s}, U^{\mathrm{br}}_{t}) = \dfrac{\sinh{(ks)} \sinh{(k(T-t))}}{k \sinh{(kT)}},\quad 0 \leq s \leq t < T$
;
$\text{Cov}(U^{\mathrm{br}}_{s}, U^{\mathrm{br}}_{t}) = \dfrac{\sinh{(ks)} \sinh{(k(T-t))}}{k \sinh{(kT)}},\quad 0 \leq s \leq t < T$
; -
(v) the paths of
 $U^{\mathrm{br}}$
are almost surely continuous.
$U^{\mathrm{br}}$
are almost surely continuous.
In what follows, we present three different representations of OU bridges. First, consider the following linear SDE:
with initial condition
![]() $U^{\mathrm{br}}_{0} = a$
. This has a unique strong solution given by
$U^{\mathrm{br}}_{0} = a$
. This has a unique strong solution given by
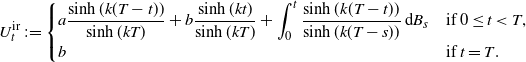 \begin{align*}U_{t}^{\mathrm{ir}} \;:\!= \begin{cases} a \dfrac{\sinh{(k(T-t))}}{\sinh{(kT)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}} + \displaystyle\int_{0}^{t} \dfrac{\sinh{(k(T-t))}}{\sinh{(k(T-s))}} \,{\mathrm{d}} B_s & \text{if $ 0 \leq t < T$,}\\b & \text{if $ t = T$.}\end{cases}\end{align*}
\begin{align*}U_{t}^{\mathrm{ir}} \;:\!= \begin{cases} a \dfrac{\sinh{(k(T-t))}}{\sinh{(kT)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}} + \displaystyle\int_{0}^{t} \dfrac{\sinh{(k(T-t))}}{\sinh{(k(T-s))}} \,{\mathrm{d}} B_s & \text{if $ 0 \leq t < T$,}\\b & \text{if $ t = T$.}\end{cases}\end{align*}
This is referred to as the integral representation (ir) of the OU bridge. The following anticipative (av) and the space–time (st) versions can be obtained by using the different representations of the Wiener bridge,
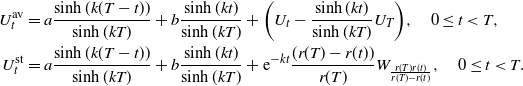 \begin{align*}U_{t}^{\mathrm{av}} & = a \dfrac{\sinh{(k(T-t))}}{\sinh{(kT)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}} +\biggl(U_t - \dfrac{\sinh{(kt)}}{\sinh{(kT)}} U_T \biggr), \quad 0 \leq t < T,\\*U_{t}^{\mathrm{st}} & = a \dfrac{\sinh{(k(T-t))}}{\sinh{(kT)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}} + {\mathrm{e}}^{-kt} \dfrac{(r(T) - r(t))}{r(T)} W_{\frac{r(T) r(t)}{ r(T) - r(t)}}, \quad 0 \leq t < T.\end{align*}
\begin{align*}U_{t}^{\mathrm{av}} & = a \dfrac{\sinh{(k(T-t))}}{\sinh{(kT)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}} +\biggl(U_t - \dfrac{\sinh{(kt)}}{\sinh{(kT)}} U_T \biggr), \quad 0 \leq t < T,\\*U_{t}^{\mathrm{st}} & = a \dfrac{\sinh{(k(T-t))}}{\sinh{(kT)}} + b \dfrac{\sinh{(kt)}}{\sinh{(kT)}} + {\mathrm{e}}^{-kt} \dfrac{(r(T) - r(t))}{r(T)} W_{\frac{r(T) r(t)}{ r(T) - r(t)}}, \quad 0 \leq t < T.\end{align*}
Now, by setting
![]() $a=b=0$
, we see that
$a=b=0$
, we see that
![]() $U_t^{\mathrm{st}} = {S}^{1,-1/r(T)}_k U_t$
. One thing to notice is that the anticipative and space–time versions are only weak solutions to (2.11), since the former requires information about the random variable
$U_t^{\mathrm{st}} = {S}^{1,-1/r(T)}_k U_t$
. One thing to notice is that the anticipative and space–time versions are only weak solutions to (2.11), since the former requires information about the random variable
![]() $U_T$
and the latter is adapted to a different filtration; see [Reference Barczy and Kern5, Section 1]. Of course,
$U_T$
and the latter is adapted to a different filtration; see [Reference Barczy and Kern5, Section 1]. Of course,
![]() $U^{\mathrm{br}}$
can be thought of as
$U^{\mathrm{br}}$
can be thought of as
![]() $(U_t, t \leq T)$
conditioned on
$(U_t, t \leq T)$
conditioned on
![]() $U_T = b$
. For conditioned processes and Markovian bridges, see [Reference Fitzsimmons, Pitman and Yor19] and [Reference Revuz and Yor32].
$U_T = b$
. For conditioned processes and Markovian bridges, see [Reference Fitzsimmons, Pitman and Yor19] and [Reference Revuz and Yor32].
3. Main result and examples
We are now ready to state the main result of this paper, which relates the distributions of the family of stopping times
to that of
![]() $T_{k}^{f}$
. We assume that
$T_{k}^{f}$
. We assume that
![]() $f \in \mathcal{C}^1((0, \infty), \mathbb{R}^+)$
, that is, it belongs to the space of continuously differentiable functions from
$f \in \mathcal{C}^1((0, \infty), \mathbb{R}^+)$
, that is, it belongs to the space of continuously differentiable functions from
![]() $(0,\infty)$
into
$(0,\infty)$
into
![]() $\mathbb{R}^+$
. This assumption is linked to Strassen’s result for the BM in [Reference Strassen39] and is crucial in ensuring that the distribution of
$\mathbb{R}^+$
. This assumption is linked to Strassen’s result for the BM in [Reference Strassen39] and is crucial in ensuring that the distribution of
![]() $T_{k}^f$
has a continuous density with respect to the Lebesgue measure on
$T_{k}^f$
has a continuous density with respect to the Lebesgue measure on
![]() $(0, \infty)$
.
$(0, \infty)$
.
Theorem 3.1. Let
![]() $f \in C^1([0,\infty), \mathbb{R})$
be such that
$f \in C^1([0,\infty), \mathbb{R})$
be such that
![]() $f(0)\neq0$
. Let
$f(0)\neq0$
. Let
![]() $\alpha\in\mathbb{R}^*, \beta \in \mathbb{R}$
. Then, for
$\alpha\in\mathbb{R}^*, \beta \in \mathbb{R}$
. Then, for
![]() $t < \zeta_{k,\alpha, \beta}$
, we have the following relationship:
$t < \zeta_{k,\alpha, \beta}$
, we have the following relationship:
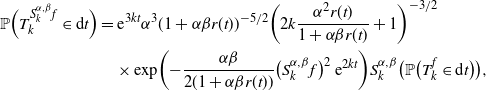 \begin{align} \mathbb{P}\Bigl( T^{{S}^{\alpha,\beta}_k f}_k \in {\mathrm{d}} t \Bigr) & = {\mathrm{e}}^{3kt} \alpha^3 (1+ \alpha \beta r(t))^{-5/2} \biggl( 2k \dfrac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \biggr)^{-3/2}\notag \\ &\quad \times \mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S^{\alpha,\beta}_k f\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) S^{\alpha,\beta}_k\bigl( \mathbb{P}\bigl( T^{ f}_k \in {\mathrm{d}} t \bigr)\bigr),\end{align}
\begin{align} \mathbb{P}\Bigl( T^{{S}^{\alpha,\beta}_k f}_k \in {\mathrm{d}} t \Bigr) & = {\mathrm{e}}^{3kt} \alpha^3 (1+ \alpha \beta r(t))^{-5/2} \biggl( 2k \dfrac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \biggr)^{-3/2}\notag \\ &\quad \times \mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S^{\alpha,\beta}_k f\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) S^{\alpha,\beta}_k\bigl( \mathbb{P}\bigl( T^{ f}_k \in {\mathrm{d}} t \bigr)\bigr),\end{align}
where
![]() $S^{\alpha,\beta}_k$
is given by (1.2).
$S^{\alpha,\beta}_k$
is given by (1.2).
Remark 3.1. As mentioned in the Introduction, focusing on the driftless OU is not restrictive. For
![]() $f\colon [0,\infty) \to \mathbb{R}$
define
$f\colon [0,\infty) \to \mathbb{R}$
define
![]() $f^*(t) \;:\!= f(t) - \mu(1 - {\mathrm{e}}^{-kt})$
,
$f^*(t) \;:\!= f(t) - \mu(1 - {\mathrm{e}}^{-kt})$
,
![]() $t \geq 0$
. Then the FPT of
$t \geq 0$
. Then the FPT of
![]() $U^{\mu}$
hitting the curve f is equal to the FPT of U hitting the curve
$U^{\mu}$
hitting the curve f is equal to the FPT of U hitting the curve
![]() $f^*$
.
$f^*$
.
Example 3.1. Theorem 3.1 of [Reference Alili, Patie and Pedersen3] gives an expression for the FPT density of an OU process starting at 0 hitting a constant threshold
![]() $f(t)=a>0$
. Writing
$f(t)=a>0$
. Writing
![]() $p_k^a(t)\,{\mathrm{d}} t = \mathbb{P}( T_{k}^{a} \in {\mathrm{d}} t )$
, we have
$p_k^a(t)\,{\mathrm{d}} t = \mathbb{P}( T_{k}^{a} \in {\mathrm{d}} t )$
, we have
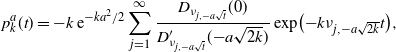 \begin{align*} p_k^a(t) = -k \,{\mathrm{e}}^{-ka^2/2} \sum_{j=1}^{\infty} \dfrac{D_{\nu_{j,-a \sqrt{t}}}(0)}{D^{\prime}_{\nu_{j, -a \sqrt{t}}} ({-}a \sqrt{2k})} \exp\bigl({-}k \nu_{j, -a \sqrt{2k} }t\bigr), \end{align*}
\begin{align*} p_k^a(t) = -k \,{\mathrm{e}}^{-ka^2/2} \sum_{j=1}^{\infty} \dfrac{D_{\nu_{j,-a \sqrt{t}}}(0)}{D^{\prime}_{\nu_{j, -a \sqrt{t}}} ({-}a \sqrt{2k})} \exp\bigl({-}k \nu_{j, -a \sqrt{2k} }t\bigr), \end{align*}
where
![]() $D_\nu (\cdot)$
is the parabolic cylinder function with index
$D_\nu (\cdot)$
is the parabolic cylinder function with index
![]() $\nu \in \mathbb{R}$
,
$\nu \in \mathbb{R}$
,
![]() $\nu_{j,b}$
is the ordered sequence of positive zeros of
$\nu_{j,b}$
is the ordered sequence of positive zeros of
![]() $D_{\nu}(b)$
,
$D_{\nu}(b)$
,
and
Here,
![]() $D_\nu (z) = 2^{-\nu/2} \,{\mathrm{e}}^{-z^2/4} H_{\nu}(z/\sqrt{2})$
, where
$D_\nu (z) = 2^{-\nu/2} \,{\mathrm{e}}^{-z^2/4} H_{\nu}(z/\sqrt{2})$
, where
![]() $H_{\nu}(\cdot)$
is the Hermite function, as found in [Reference Lebedev and Silverman24, page 285]. Now, we use
$H_{\nu}(\cdot)$
is the Hermite function, as found in [Reference Lebedev and Silverman24, page 285]. Now, we use
![]() $S^{\alpha,\beta}_k$
to get the following family of curves:
$S^{\alpha,\beta}_k$
to get the following family of curves:
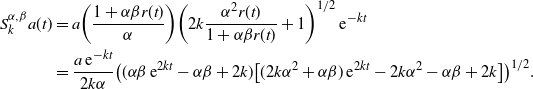 \begin{align*}S^{\alpha,\beta}_k a(t) & = a \biggl(\dfrac{1+ \alpha \beta r(t)}{\alpha} \biggr)\biggl(2k \dfrac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \biggr)^{1/2} \,{\mathrm{e}}^{-kt} \\ & = \dfrac{a \,{\mathrm{e}}^{-kt}}{2k \alpha} \bigl( (\alpha \beta \,{\mathrm{e}}^{2kt} - \alpha \beta + 2k)\bigl[(2k\alpha^2+\alpha \beta) \,{\mathrm{e}}^{2kt} - 2k \alpha^2 -\alpha \beta +2k\bigr] \bigr)^{1/2}.\end{align*}
\begin{align*}S^{\alpha,\beta}_k a(t) & = a \biggl(\dfrac{1+ \alpha \beta r(t)}{\alpha} \biggr)\biggl(2k \dfrac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \biggr)^{1/2} \,{\mathrm{e}}^{-kt} \\ & = \dfrac{a \,{\mathrm{e}}^{-kt}}{2k \alpha} \bigl( (\alpha \beta \,{\mathrm{e}}^{2kt} - \alpha \beta + 2k)\bigl[(2k\alpha^2+\alpha \beta) \,{\mathrm{e}}^{2kt} - 2k \alpha^2 -\alpha \beta +2k\bigr] \bigr)^{1/2}.\end{align*}
Such curves for
![]() $\beta=1, \; k=1/2, \; a=1$
and different values of
$\beta=1, \; k=1/2, \; a=1$
and different values of
![]() $\alpha$
are plotted in Figure 2. By our Theorem 3.1, we can write
$\alpha$
are plotted in Figure 2. By our Theorem 3.1, we can write
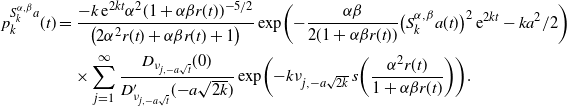 \begin{align}\nonumber p_k^{S^{\alpha,\beta}_k a}(t) & = \dfrac{-k \,{\mathrm{e}}^{2kt} \alpha^2(1+ \alpha \beta r(t))^{-5/2}}{\big(2\alpha^2r(t)+ \alpha\beta r(t) + 1\big)} \exp\biggl({-} \dfrac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S^{\alpha,\beta}_k a(t)\bigr)^2 \,{\mathrm{e}}^{2kt} - ka^2/2\biggr)\\ &\quad \times \sum_{j=1}^{\infty} \dfrac{D_{\nu_{j,-a \sqrt{t}}}(0)}{D^{\prime}_{\nu_{j, -a \sqrt{t}}} ({-}a \sqrt{2k})} \exp\biggl({-}k \nu_{j, -a \sqrt{2k} } \; s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr).\end{align}
\begin{align}\nonumber p_k^{S^{\alpha,\beta}_k a}(t) & = \dfrac{-k \,{\mathrm{e}}^{2kt} \alpha^2(1+ \alpha \beta r(t))^{-5/2}}{\big(2\alpha^2r(t)+ \alpha\beta r(t) + 1\big)} \exp\biggl({-} \dfrac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S^{\alpha,\beta}_k a(t)\bigr)^2 \,{\mathrm{e}}^{2kt} - ka^2/2\biggr)\\ &\quad \times \sum_{j=1}^{\infty} \dfrac{D_{\nu_{j,-a \sqrt{t}}}(0)}{D^{\prime}_{\nu_{j, -a \sqrt{t}}} ({-}a \sqrt{2k})} \exp\biggl({-}k \nu_{j, -a \sqrt{2k} } \; s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr).\end{align}
Note that the considered values of
![]() $\alpha,\beta$
and k satisfy case (ii) of Theorem 6.1, yielding transient curves and thus FPT distributions that are improper. In the special case of
$\alpha,\beta$
and k satisfy case (ii) of Theorem 6.1, yielding transient curves and thus FPT distributions that are improper. In the special case of
![]() $\alpha \beta = 2k,$
we get the family of curves
$\alpha \beta = 2k,$
we get the family of curves
with FPT density given by
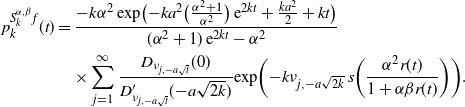 \begin{align*} p_k^{S^{\alpha,\beta}_k f}(t)& = \dfrac{-k \alpha^2 \,\mathrm{{exp}}\bigl({-k a^2 \bigl(\frac{\alpha^2 +1}{\alpha^2} \bigr) \,{\mathrm{e}}^{2kt}+ \frac{k a^2}{2}+kt}\bigr)}{(\alpha^2 +1)\,{\mathrm{e}}^{2kt}-\alpha^2} \\ &\quad \times \sum_{j=1}^{\infty} \dfrac{D_{\nu_{j,-a \sqrt{t}}}(0)}{D^{\prime}_{\nu_{j, -a \sqrt{t}}} ({-}a \sqrt{2k})} \mathrm{{exp}}\biggl({-k \nu_{j, -a \sqrt{2k} } \; s\biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)}\biggr).\end{align*}
\begin{align*} p_k^{S^{\alpha,\beta}_k f}(t)& = \dfrac{-k \alpha^2 \,\mathrm{{exp}}\bigl({-k a^2 \bigl(\frac{\alpha^2 +1}{\alpha^2} \bigr) \,{\mathrm{e}}^{2kt}+ \frac{k a^2}{2}+kt}\bigr)}{(\alpha^2 +1)\,{\mathrm{e}}^{2kt}-\alpha^2} \\ &\quad \times \sum_{j=1}^{\infty} \dfrac{D_{\nu_{j,-a \sqrt{t}}}(0)}{D^{\prime}_{\nu_{j, -a \sqrt{t}}} ({-}a \sqrt{2k})} \mathrm{{exp}}\biggl({-k \nu_{j, -a \sqrt{2k} } \; s\biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)}\biggr).\end{align*}
An alternative expression for (3.2) can be obtained by using Theorem 3.1 with the semi-explicit expression for
![]() $p_k^a$
provided in [Reference Ricciardi, Sacerdote and Sato34].
$p_k^a$
provided in [Reference Ricciardi, Sacerdote and Sato34].
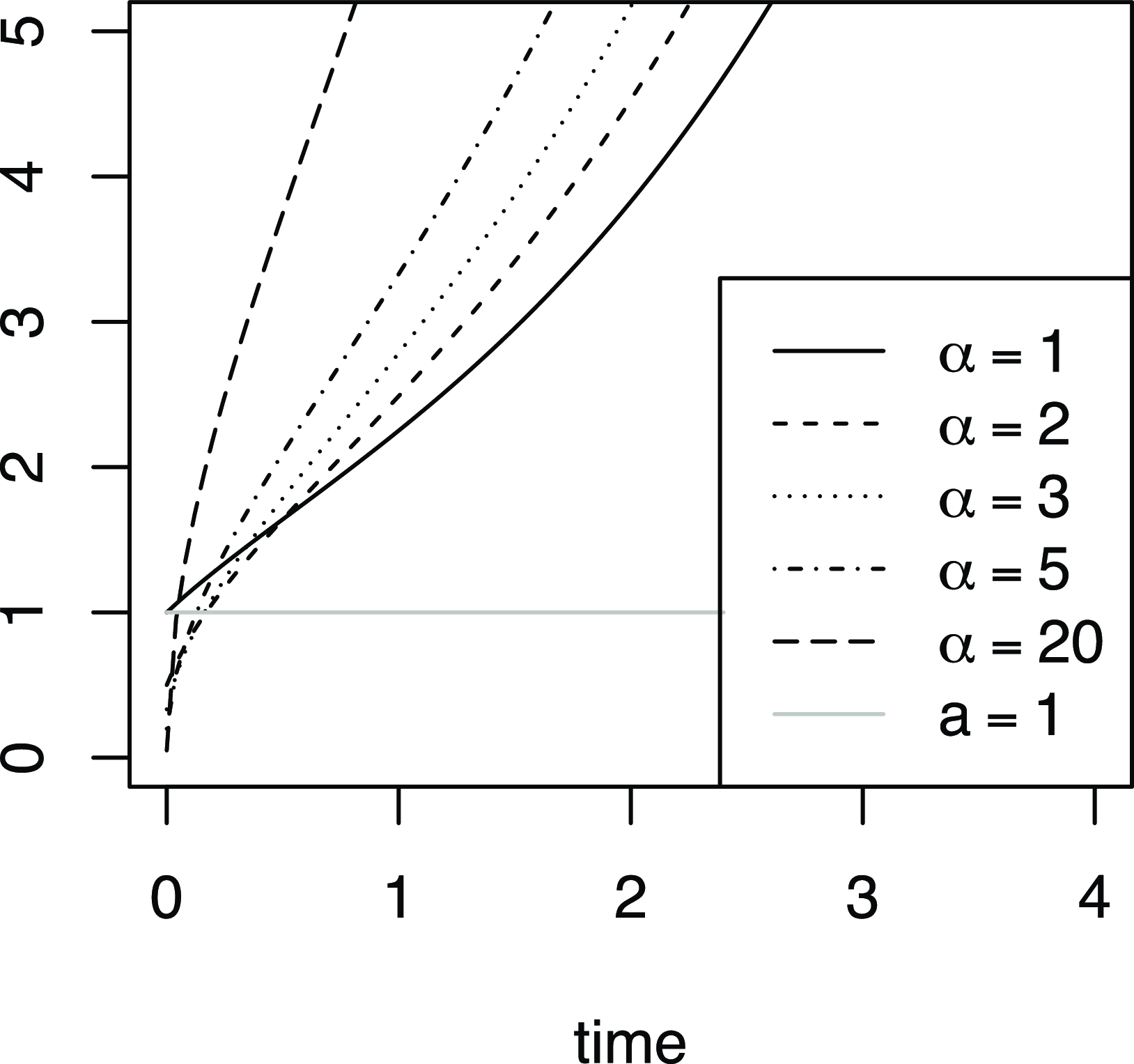
Figure 2.
![]() ${S}^{\alpha,1}_{1/2} a$
for
${S}^{\alpha,1}_{1/2} a$
for
![]() $a=$
1,
$a=$
1,
![]() $\beta=1$
,
$\beta=1$
,
![]() $ k=1/2$
, and different values of
$ k=1/2$
, and different values of
![]() $\alpha$
, in particular
$\alpha$
, in particular
![]() $\alpha=1$
(solid line),
$\alpha=1$
(solid line),
![]() $\alpha=2$
(short-dashed line),
$\alpha=2$
(short-dashed line),
![]() $\alpha=3$
(dotted line),
$\alpha=3$
(dotted line),
![]() $\alpha=5$
(dot-dashed line),
$\alpha=5$
(dot-dashed line),
![]() $\alpha=20$
(long-dashed line).
$\alpha=20$
(long-dashed line).
Example 3.2. By Theorem 2.1 of [Reference Groeneboom20], the law of the first time when a BM hits a parabolic curve of the form
![]() $f_{a,b}(t)= a + bt^2$
, for
$f_{a,b}(t)= a + bt^2$
, for
![]() $a,b>0$
, is given by
$a,b>0$
, is given by
where
![]() $h_{b,a}\colon \mathbb{R}^{+} \to \mathbb{R}^{+}$
is characterised by the Laplace transform
$h_{b,a}\colon \mathbb{R}^{+} \to \mathbb{R}^{+}$
is characterised by the Laplace transform
and Ai denotes the Airy function of the first kind, as introduced in [Reference Lebedev and Silverman24, page 136]. By the scaling property of the BM, we have
where
![]() $\stackrel{d}{=}$
denotes equality in distribution, and so we can use the series expansion given in [Reference Alili and Patie1, example 4.1.2] for the density of
$\stackrel{d}{=}$
denotes equality in distribution, and so we can use the series expansion given in [Reference Alili and Patie1, example 4.1.2] for the density of
![]() $T^{f_{1,ba^3}}$
to get
$T^{f_{1,ba^3}}$
to get
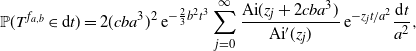 \begin{equation} \mathbb{P}( T^{f_{a,b}} \in {\mathrm{d}} t ) = 2 (c ba^3 )^2 \,{\mathrm{e}}^{- \frac{2}{3} b^2 t^3} \sum_{j=0}^{\infty} \dfrac{\mathrm{Ai} (z_j + 2c ba^3 )}{\mathrm{Ai}^{\prime}(z_j )} \,{\mathrm{e}}^{-z_j t/a^2} \dfrac{{\mathrm{d}} t}{a^2},\end{equation}
\begin{equation} \mathbb{P}( T^{f_{a,b}} \in {\mathrm{d}} t ) = 2 (c ba^3 )^2 \,{\mathrm{e}}^{- \frac{2}{3} b^2 t^3} \sum_{j=0}^{\infty} \dfrac{\mathrm{Ai} (z_j + 2c ba^3 )}{\mathrm{Ai}^{\prime}(z_j )} \,{\mathrm{e}}^{-z_j t/a^2} \dfrac{{\mathrm{d}} t}{a^2},\end{equation}
where
![]() $(z_j)_{j \geq 0}$
is the decreasing sequence of negative zeros of the function
$(z_j)_{j \geq 0}$
is the decreasing sequence of negative zeros of the function
![]() $\mathrm{Ai}(\cdot)$
and
$\mathrm{Ai}(\cdot)$
and
![]() $c=(2 ba^3)^{-1/3}$
. Now, the FPT problem for this curve is equivalent to the FPT problem of the OU hitting the curve
$c=(2 ba^3)^{-1/3}$
. Now, the FPT problem for this curve is equivalent to the FPT problem of the OU hitting the curve
![]() $g(t) \;:\!= \Lambda_{k}^{-1}f_{a,b}(t) = {\mathrm{e}}^{-kt} (a + b r^2(t))$
, with its FPT law given by
$g(t) \;:\!= \Lambda_{k}^{-1}f_{a,b}(t) = {\mathrm{e}}^{-kt} (a + b r^2(t))$
, with its FPT law given by
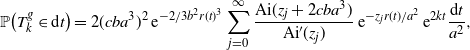 \begin{align*}\mathbb{P} \bigl(T_{k}^g \in {\mathrm{d}} t \bigr) = 2 (c ba^3 )^2 \,{\mathrm{e}}^{-2/3 b^2 r(t)^3} \sum_{j=0}^{\infty} \dfrac{\mathrm{Ai} (z_j + 2c ba^3 )}{\mathrm{Ai}^{\prime} (z_j )} \,{\mathrm{e}}^{-z_j r(t)/a^2} \,{\mathrm{e}}^{2kt} \dfrac{{\mathrm{d}} t}{a^2},\end{align*}
\begin{align*}\mathbb{P} \bigl(T_{k}^g \in {\mathrm{d}} t \bigr) = 2 (c ba^3 )^2 \,{\mathrm{e}}^{-2/3 b^2 r(t)^3} \sum_{j=0}^{\infty} \dfrac{\mathrm{Ai} (z_j + 2c ba^3 )}{\mathrm{Ai}^{\prime} (z_j )} \,{\mathrm{e}}^{-z_j r(t)/a^2} \,{\mathrm{e}}^{2kt} \dfrac{{\mathrm{d}} t}{a^2},\end{align*}
which is obtained using (3.3) and (5.1). Applying the transformation
![]() $S^{\alpha,\beta}_k$
to g, we get the family of curves
$S^{\alpha,\beta}_k$
to g, we get the family of curves
Recalling the notation
![]() $p_k^g(t)\,{\mathrm{d}} t = \mathbb{P}\bigl( T_{k}^{g} \in {\mathrm{d}} t \bigr)$
, applying Theorem 3.1 and simplifying, we obtain
$p_k^g(t)\,{\mathrm{d}} t = \mathbb{P}\bigl( T_{k}^{g} \in {\mathrm{d}} t \bigr)$
, applying Theorem 3.1 and simplifying, we obtain
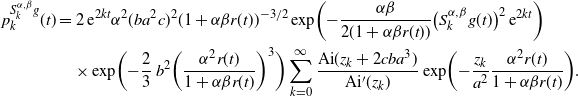 \begin{align*} p_k^{S^{\alpha,\beta}_k g}(t) & = 2\,{\mathrm{e}}^{2kt} \alpha^2 (ba^2 c )^2(1+ \alpha \beta r(t))^{-3/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S_{k}^{\alpha,\beta}g(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) \\ &\quad \times \mathrm{{exp}}\biggl({-\frac23 \; b^2 \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)^3}\biggr) \sum_{k=0}^{\infty} \dfrac{\mathrm{Ai}(z_k + 2c ba^3)}{\mathrm{Ai}^{\prime}(z_k)} \,\mathrm{{exp}}\biggl({- \frac{z_k}{a^2} \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} }\biggr).\end{align*}
\begin{align*} p_k^{S^{\alpha,\beta}_k g}(t) & = 2\,{\mathrm{e}}^{2kt} \alpha^2 (ba^2 c )^2(1+ \alpha \beta r(t))^{-3/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S_{k}^{\alpha,\beta}g(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) \\ &\quad \times \mathrm{{exp}}\biggl({-\frac23 \; b^2 \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)^3}\biggr) \sum_{k=0}^{\infty} \dfrac{\mathrm{Ai}(z_k + 2c ba^3)}{\mathrm{Ai}^{\prime}(z_k)} \,\mathrm{{exp}}\biggl({- \frac{z_k}{a^2} \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} }\biggr).\end{align*}
4. Properties of the transformations
We now state a result that gives an insight into our
![]() $S^{\alpha,\beta}_k$
transformation.
$S^{\alpha,\beta}_k$
transformation.
Lemma 4.1.
-
(1) Let
 $(\alpha, \beta)$
and
$(\alpha, \beta)$
and
 $(\alpha^{\prime}, \beta^{\prime}) \in \mathbb{R}^{*} \times \mathbb{R}$
and
$(\alpha^{\prime}, \beta^{\prime}) \in \mathbb{R}^{*} \times \mathbb{R}$
and
 $A_{k,\infty}$
be defined as in (2.6). The mapping
$A_{k,\infty}$
be defined as in (2.6). The mapping
 $S^{\alpha,\beta}_k\colon A_{k,\infty} \to A_{k,\infty}$
defined by (2.10) admits representation (1.2) and satisfies (4.1)In particular,
$S^{\alpha,\beta}_k\colon A_{k,\infty} \to A_{k,\infty}$
defined by (2.10) admits representation (1.2) and satisfies (4.1)In particular, \begin{equation} S^{\alpha, \beta}_k \circ S^{\alpha^{\prime}, \beta^{\prime}}_{k} = S^{\alpha \alpha^{\prime}, \alpha \beta^{\prime} + {{\beta}/{\alpha^{\prime}}}}_{k}.\end{equation}
\begin{equation} S^{\alpha, \beta}_k \circ S^{\alpha^{\prime}, \beta^{\prime}}_{k} = S^{\alpha \alpha^{\prime}, \alpha \beta^{\prime} + {{\beta}/{\alpha^{\prime}}}}_{k}.\end{equation}
 $\bigl(S^{1,\beta}_{k}\bigr)_{\beta\in\mathbb{R}}$
and
$\bigl(S^{1,\beta}_{k}\bigr)_{\beta\in\mathbb{R}}$
and
 $\bigl( S^{{\mathrm{e}}^\alpha,0}_{k}\bigr)_{\alpha\in\mathbb{R}}$
are groups. Furthermore, for
$\bigl( S^{{\mathrm{e}}^\alpha,0}_{k}\bigr)_{\alpha\in\mathbb{R}}$
are groups. Furthermore, for
 $a,b>0$
and
$a,b>0$
and
 $A_{k}(a,b)$
defined as in (2.7), if
$A_{k}(a,b)$
defined as in (2.7), if
 $f \in A_{k}(a,b)$
, then
$f \in A_{k}(a,b)$
, then
 $S^{\alpha, \beta}_{k}f \in A_{k} \bigl(a_{\alpha, \beta}, b_{\alpha, \beta}^f \bigr)$
, where we set and for
$S^{\alpha, \beta}_{k}f \in A_{k} \bigl(a_{\alpha, \beta}, b_{\alpha, \beta}^f \bigr)$
, where we set and for \begin{align*} a_{\alpha, \beta} = \begin{cases} \dfrac{a}{\alpha^2 - \alpha \beta a} & \text{if $ \alpha^2 - \alpha \beta a>0$, $ k \geq 0 $,}\\ \dfrac{a}{\alpha^2 - (\alpha \beta + 2k \alpha^2)a} & \text{if $ 0<\dfrac{2k a}{(\alpha \beta + 2k \alpha^2)a - \alpha^2}<1$, $ k<0 $,}\\ + \infty & \text{otherwise,}\end{cases}\end{align*}
\begin{align*} a_{\alpha, \beta} = \begin{cases} \dfrac{a}{\alpha^2 - \alpha \beta a} & \text{if $ \alpha^2 - \alpha \beta a>0$, $ k \geq 0 $,}\\ \dfrac{a}{\alpha^2 - (\alpha \beta + 2k \alpha^2)a} & \text{if $ 0<\dfrac{2k a}{(\alpha \beta + 2k \alpha^2)a - \alpha^2}<1$, $ k<0 $,}\\ + \infty & \text{otherwise,}\end{cases}\end{align*}
 $f \in A_{k,\infty}$
we wrote Observe that
$f \in A_{k,\infty}$
we wrote Observe that \begin{align*} b_{\alpha, \beta}^f = \begin{cases}b & \text{if $\alpha^2 - \alpha \beta b >0$, $ k\geq0$,} \\\dfrac{b}{1-2kb} & \text{if $ 0<\dfrac{2k b}{(\alpha \beta + 2k \alpha^2)b - \alpha^2}<1$, $ k<0$,} \\ \rho \circ \tau f\biggl(s\biggl(\dfrac{\alpha}{\beta}\biggr)\biggr) & \text{otherwise.}\end{cases}\end{align*}
\begin{align*} b_{\alpha, \beta}^f = \begin{cases}b & \text{if $\alpha^2 - \alpha \beta b >0$, $ k\geq0$,} \\\dfrac{b}{1-2kb} & \text{if $ 0<\dfrac{2k b}{(\alpha \beta + 2k \alpha^2)b - \alpha^2}<1$, $ k<0$,} \\ \rho \circ \tau f\biggl(s\biggl(\dfrac{\alpha}{\beta}\biggr)\biggr) & \text{otherwise.}\end{cases}\end{align*}
 $a_{\alpha, \beta} \to r(\zeta_{k,\alpha, \beta})$
as
$a_{\alpha, \beta} \to r(\zeta_{k,\alpha, \beta})$
as
 $a \to \infty$
.
$a \to \infty$
.
-
(2) Let
 $\mu$
be a positive Radon measure on
$\mu$
be a positive Radon measure on
 $\mathbb{R}^{+}$
. Then there exists a unique positive and differentiable function
$\mathbb{R}^{+}$
. Then there exists a unique positive and differentiable function
 $\mathfrak{f}$
with
$\mathfrak{f}$
with
 $\mathfrak{f}(0)=1$
and
$\mathfrak{f}(0)=1$
and
 $\mathfrak{f}^{\prime}+ k \mathfrak{f} + {{k}/{((2k \tau \mathfrak{f}+1)\mathfrak{f})}}> 0$
, which satisfies the following nonlinear differential equation (4.2)where f ′′ is the second derivative in the sense of distributions. Moreover,
$\mathfrak{f}^{\prime}+ k \mathfrak{f} + {{k}/{((2k \tau \mathfrak{f}+1)\mathfrak{f})}}> 0$
, which satisfies the following nonlinear differential equation (4.2)where f ′′ is the second derivative in the sense of distributions. Moreover, \begin{equation} f^3 f^{\prime\prime} - k^2 f^4= \dfrac{-\mu(s(\tau f)) + k^2}{(2 k (\tau f)+1)^2},\end{equation}
spans the set of positive solutions of (4.2).
\begin{equation} f^3 f^{\prime\prime} - k^2 f^4= \dfrac{-\mu(s(\tau f)) + k^2}{(2 k (\tau f)+1)^2},\end{equation}
spans the set of positive solutions of (4.2). \begin{align*} \bigl\{S^{\alpha,\beta}_k \mathfrak{f};\, \alpha>0, \beta \in \mathbb{R} \bigr\} \end{align*}
\begin{align*} \bigl\{S^{\alpha,\beta}_k \mathfrak{f};\, \alpha>0, \beta \in \mathbb{R} \bigr\} \end{align*}
Before proving Lemma 4.1, we start by discussing some of the properties of
![]() $\Sigma_{k}$
and
$\Sigma_{k}$
and
![]() $\Pi^{\alpha,\beta} $
.
$\Pi^{\alpha,\beta} $
.
Proposition 4.1. For any
![]() $a,b>0$
and
$a,b>0$
and
![]() $f \in A_{k,\infty}$
, we have the following assertions.
$f \in A_{k,\infty}$
, we have the following assertions.
-
(1)
 $\Sigma_{k}$
is an involution operator, i.e.
$\Sigma_{k}$
is an involution operator, i.e.
 $\Sigma_{k} \circ \Sigma_{k} = \mathrm{Id}$
on
$\Sigma_{k} \circ \Sigma_{k} = \mathrm{Id}$
on
 $A_{k,\infty}$
.
$A_{k,\infty}$
. -
(2)
 $\tau f (t) = r(\rho \circ \tau \circ \Sigma_{k} f(r(t)))$
.
$\tau f (t) = r(\rho \circ \tau \circ \Sigma_{k} f(r(t)))$
. -
(3)
 $\Sigma_{k}(A_{k}(a,b)) = A_{k}(b, a)$
.
$\Sigma_{k}(A_{k}(a,b)) = A_{k}(b, a)$
. -
(4)
 $\Pi^{\alpha,\beta} \Lambda_{k} = \Lambda_{k} \Pi^{\alpha,\beta} $
.
$\Pi^{\alpha,\beta} \Lambda_{k} = \Lambda_{k} \Pi^{\alpha,\beta} $
.
Proof. (1) The involution property follows from (2.8) and the fact that
![]() $\Sigma$
is an involution.
$\Sigma$
is an involution.
(2) By using (2.9), we obtain
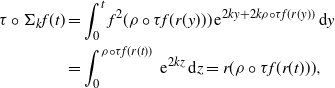 \begin{align*} \tau \circ \Sigma_{k}f(t) & = \int_{0}^{t} f^2(\rho \circ \tau f(r(y))) \,{\mathrm{e}}^{2ky + 2k \rho \circ \tau f(r(y))} \,{\mathrm{d}} y \\ & = \int_{0}^{\rho \circ \tau f(r(t))} \,{\mathrm{e}}^{2kz} \,{\mathrm{d}} z = r(\rho \circ \tau f(r(t))),\end{align*}
\begin{align*} \tau \circ \Sigma_{k}f(t) & = \int_{0}^{t} f^2(\rho \circ \tau f(r(y))) \,{\mathrm{e}}^{2ky + 2k \rho \circ \tau f(r(y))} \,{\mathrm{d}} y \\ & = \int_{0}^{\rho \circ \tau f(r(t))} \,{\mathrm{e}}^{2kz} \,{\mathrm{d}} z = r(\rho \circ \tau f(r(t))),\end{align*}
where we used a change of variables in the second equality. The assertion follows using the fact that
![]() $\Sigma_{k}$
is an involution.
$\Sigma_{k}$
is an involution.
(3) First, consider
![]() $k<0$
and take
$k<0$
and take
![]() $f \in A_{k}(a,b)$
. Observe that
$f \in A_{k}(a,b)$
. Observe that
![]() $\rho \circ \tau f(b/(1-2kb)) = -s({-}a)$
. Now, by part (2),
$\rho \circ \tau f(b/(1-2kb)) = -s({-}a)$
. Now, by part (2),
![]() $\tau \circ \Sigma_{k}f({-}s({-}b)) = r(\rho \circ \tau f(b/(1-2kb)) = a/(1-2ka)$
and so
$\tau \circ \Sigma_{k}f({-}s({-}b)) = r(\rho \circ \tau f(b/(1-2kb)) = a/(1-2ka)$
and so
![]() $\Sigma_{k}f \in A_{k}(b,a)$
. Similarly, the result holds for
$\Sigma_{k}f \in A_{k}(b,a)$
. Similarly, the result holds for
![]() $k>0$
.
$k>0$
.
(4) Here,
which follows by a change of variable. The identity can easily be derived now.
Proof of Lemma 4.1. (1) Starting from the definition of
![]() $S_k^{\alpha,\beta}$
in (2.10) and using the decomposition of
$S_k^{\alpha,\beta}$
in (2.10) and using the decomposition of
![]() $\Sigma_k$
in (2.8), identity (4) from Proposition 4.1 and the decomposition of
$\Sigma_k$
in (2.8), identity (4) from Proposition 4.1 and the decomposition of
![]() $S^{\alpha,\beta}$
given in (2.3), we can write
$S^{\alpha,\beta}$
given in (2.3), we can write
Now, if we use the functional definitions of the operators, we get the representation (1.2), as illustrated earlier in Figure 1. Next, property (4.1) follows from the similar group property of the family of operators
![]() $(S^{\alpha, \beta})_{(\alpha , \beta) \in \mathbb{R}^* \times \mathbb{R}}$
, as stated in Section 2.1; see also [Reference Alili and Patie2, Proposition 2.3]. Lastly, using the identity
$(S^{\alpha, \beta})_{(\alpha , \beta) \in \mathbb{R}^* \times \mathbb{R}}$
, as stated in Section 2.1; see also [Reference Alili and Patie2, Proposition 2.3]. Lastly, using the identity
which follows readily by a change of variables, we find that if
![]() $f \in A_{k}(a,b)$
, then
$f \in A_{k}(a,b)$
, then
![]() $S_{k}^{\alpha, \beta}f \in A_{k}\bigl(a_{\alpha, \beta}, b_{\alpha, \beta}^f\bigr)$
.
$S_{k}^{\alpha, \beta}f \in A_{k}\bigl(a_{\alpha, \beta}, b_{\alpha, \beta}^f\bigr)$
.
(2) As discussed in Section 2.2, if
![]() $\phi$
solves the Sturm–Liouville equation (2.5), then the vectorial space
$\phi$
solves the Sturm–Liouville equation (2.5), then the vectorial space
![]() $\{\Pi^{\alpha,\beta} \phi ;\, \alpha, \beta \in \mathbb{R}\}$
is the set of solutions to the same equation. Moreover, all positive solutions are convex and are described by the set
$\{\Pi^{\alpha,\beta} \phi ;\, \alpha, \beta \in \mathbb{R}\}$
is the set of solutions to the same equation. Moreover, all positive solutions are convex and are described by the set
![]() $\{\Pi^{\alpha,\beta} \varphi ;\, \alpha>0, \beta \geq 0\}$
, where
$\{\Pi^{\alpha,\beta} \varphi ;\, \alpha>0, \beta \geq 0\}$
, where
![]() $\varphi$
is the unique, positive, decreasing solution such that
$\varphi$
is the unique, positive, decreasing solution such that
![]() $\varphi(0)=1$
. Now, we need to show that the image of (4.2) by
$\varphi(0)=1$
. Now, we need to show that the image of (4.2) by
![]() $\Sigma_{k}$
is (2.5) and vice versa. Let
$\Sigma_{k}$
is (2.5) and vice versa. Let
![]() $\phi(t) = \Sigma_{k}f(t)$
. Then, we obtain
$\phi(t) = \Sigma_{k}f(t)$
. Then, we obtain
![]() $\phi(s(\tau f(t))) f(t) = {\mathrm{e}}^{-k s(\tau f(t)) - kt}$
. Differentiating each side once, we get
$\phi(s(\tau f(t))) f(t) = {\mathrm{e}}^{-k s(\tau f(t)) - kt}$
. Differentiating each side once, we get
Differentiating again, we obtain
So if
![]() $\phi$
satisfies (2.5), we get (4.2) and vice versa. Now, by letting
$\phi$
satisfies (2.5), we get (4.2) and vice versa. Now, by letting
![]() $\mathfrak{f} = \Sigma_{k} \varphi$
, we see that it satisfies the required properties.
$\mathfrak{f} = \Sigma_{k} \varphi$
, we see that it satisfies the required properties.
5. Proofs of Theorem 3.1
We provide three different proofs of Theorem 3.1. The first method is a direct approach that uses results from [Reference Alili and Patie2]. The second approach uses a generalisation of the so-called Gauss–Markov processes and gives an insight into some of the results given in Lemma 4.1. The third proof relies on the Lie group techniques applied to the Fokker–Planck equation (1.3). We also mention that, similarly to the BM case, it is sufficient to consider only the case where
![]() $\alpha>0$
. This is because, by the symmetry of the BM and the OU process starting at 0 without drift, hitting negative- or positive-valued thresholds for the first time has the same probability. Hence, for any
$\alpha>0$
. This is because, by the symmetry of the BM and the OU process starting at 0 without drift, hitting negative- or positive-valued thresholds for the first time has the same probability. Hence, for any
![]() $(\alpha,\beta) \in \mathbb{R}^{*} \times \mathbb{R}$
, we have
$(\alpha,\beta) \in \mathbb{R}^{*} \times \mathbb{R}$
, we have
5.1. First proof of Theorem 3.1
First proof of Theorem 3.1. We aim to use (2.1), which connects the FPT distribution of
![]() $ S^{\alpha,\beta} f$
to that of f. We can connect the FPTs of OU and BM in the following manner:
$ S^{\alpha,\beta} f$
to that of f. We can connect the FPTs of OU and BM in the following manner:
Note that
Writing
![]() $p_k^{f}(t) \,{\mathrm{d}} t = \mathbb{P}\bigl( T_{k}^{ f} \in {\mathrm{d}} t \bigr)$
and
$p_k^{f}(t) \,{\mathrm{d}} t = \mathbb{P}\bigl( T_{k}^{ f} \in {\mathrm{d}} t \bigr)$
and
![]() $p^{f}(t) \,{\mathrm{d}} t = \mathbb{P}( T^{f} \in {\mathrm{d}} t )$
, we get
$p^{f}(t) \,{\mathrm{d}} t = \mathbb{P}( T^{f} \in {\mathrm{d}} t )$
, we get
Now, using (2.1) and (2.2), we can rewrite the right-hand side as follows:
 \begin{align} & p^{S^{\alpha,\beta} \Lambda_{k} f}(r(t))\notag \\ & \quad = \alpha^3 (1+ \alpha \beta r(t))^{-5/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} (S^{\alpha,\beta} \Lambda_{k} f(r(t)))^2}\biggr) S^{\alpha,\beta} \bigl( p^{\Lambda_{k} f}(r(t))\bigr) \notag \\ & \quad = \alpha^2 (1+ \alpha \beta r(t))^{-3/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} (S^{\alpha,\beta} \Lambda_{k} f(r(t)))^2}\biggr) p^{\Lambda_{k} f} \biggl(\dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr).\end{align}
\begin{align} & p^{S^{\alpha,\beta} \Lambda_{k} f}(r(t))\notag \\ & \quad = \alpha^3 (1+ \alpha \beta r(t))^{-5/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} (S^{\alpha,\beta} \Lambda_{k} f(r(t)))^2}\biggr) S^{\alpha,\beta} \bigl( p^{\Lambda_{k} f}(r(t))\bigr) \notag \\ & \quad = \alpha^2 (1+ \alpha \beta r(t))^{-3/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} (S^{\alpha,\beta} \Lambda_{k} f(r(t)))^2}\biggr) p^{\Lambda_{k} f} \biggl(\dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr).\end{align}
By using (5.1), we get
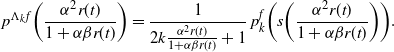 \begin{equation} p^{\Lambda_{k} f} \biggl(\dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) = \dfrac{1}{2k \frac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1} \; p_k^{f} \biggl( s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr).\end{equation}
\begin{equation} p^{\Lambda_{k} f} \biggl(\dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) = \dfrac{1}{2k \frac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1} \; p_k^{f} \biggl( s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr).\end{equation}
Notice that
![]() $S^{\alpha,\beta} \Lambda_{k} f(r(t)) = {\mathrm{e}}^{kt} S_{k}^{\alpha,\beta}f(t) $
. Now, plugging (5.4) into (5.3) and then into (5.2), we get
$S^{\alpha,\beta} \Lambda_{k} f(r(t)) = {\mathrm{e}}^{kt} S_{k}^{\alpha,\beta}f(t) $
. Now, plugging (5.4) into (5.3) and then into (5.2), we get
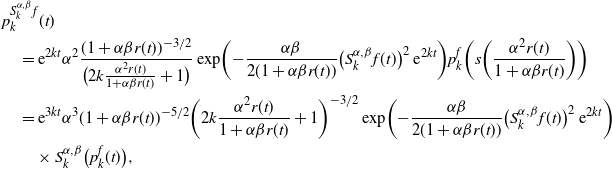 \begin{align*} & p_k^{ S_{k}^{\alpha,\beta}f}(t) \\ &\quad = {\mathrm{e}}^{2kt} \alpha^2 \dfrac{(1+ \alpha \beta r(t))^{-3/2}}{\bigl(2k \frac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \bigr)} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S_{k}^{\alpha,\beta}f(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) p_k^{f} \biggl( s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr)\\&\quad = {\mathrm{e}}^{3kt} \alpha^3 (1+ \alpha \beta r(t))^{-5/2} \biggl(2k \dfrac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \biggr)^{-3/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S_{k}^{\alpha,\beta}f(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) \\ & \quad\quad \times S_{k}^{\alpha,\beta} \bigl(p_k^{f}(t) \bigr),\end{align*}
\begin{align*} & p_k^{ S_{k}^{\alpha,\beta}f}(t) \\ &\quad = {\mathrm{e}}^{2kt} \alpha^2 \dfrac{(1+ \alpha \beta r(t))^{-3/2}}{\bigl(2k \frac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \bigr)} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S_{k}^{\alpha,\beta}f(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) p_k^{f} \biggl( s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr)\\&\quad = {\mathrm{e}}^{3kt} \alpha^3 (1+ \alpha \beta r(t))^{-5/2} \biggl(2k \dfrac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \biggr)^{-3/2} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(S_{k}^{\alpha,\beta}f(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) \\ & \quad\quad \times S_{k}^{\alpha,\beta} \bigl(p_k^{f}(t) \bigr),\end{align*}
where we used (1.2) to obtain the last equation.
5.2. Second proof of Theorem 3.1
We take
![]() $\phi \in A_{k}(a,b) \cap AC([0,b))$
, where AC([0,b)) is the space of absolutely continuous functions on [0,b). We introduce the process
$\phi \in A_{k}(a,b) \cap AC([0,b))$
, where AC([0,b)) is the space of absolutely continuous functions on [0,b). We introduce the process
![]() $X\;:\!= (X_t)_{0 \leq t <b}$
to be the generalised Gauss–Markov process of OU type with parameters
$X\;:\!= (X_t)_{0 \leq t <b}$
to be the generalised Gauss–Markov process of OU type with parameters
![]() $(\phi,k)$
, which is defined as the unique strong solution to the following SDE
$(\phi,k)$
, which is defined as the unique strong solution to the following SDE
with
![]() $X_0=x \in \mathbb{R}$
, that is,
$X_0=x \in \mathbb{R}$
, that is,
We also let
denote the family of probability measures corresponding to the process X. We assume throughout that
![]() $\phi(0) = 1$
. Notice that when
$\phi(0) = 1$
. Notice that when
![]() $\phi(t) = {\mathrm{e}}^{-kt}$
, we get
$\phi(t) = {\mathrm{e}}^{-kt}$
, we get
![]() $X_t = W_{r(t)}$
, where
$X_t = W_{r(t)}$
, where
![]() $(W_t, t \geq 0)$
is another BM.
$(W_t, t \geq 0)$
is another BM.
Lemma 5.1. For any
![]() $y \in \mathbb{R}$
, set
$y \in \mathbb{R}$
, set
Then, for any
![]() $f \in A_k(a,b)$
, setting
$f \in A_k(a,b)$
, setting
![]() $\phi = \Sigma_{k}f$
, the identity
$\phi = \Sigma_{k}f$
, the identity
holds almost surely.
Proof. Using (1.1), we have a.s.
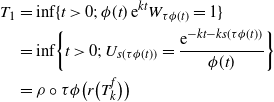 \begin{align*}T_{1} & = \inf \{t >0 ; \;\phi(t) \,{\mathrm{e}}^{kt} W_{\tau \phi(t)} = 1 \}\\ &= \inf \biggl\{t>0 ; \; U_{s(\tau \phi(t))}= \dfrac{{\mathrm{e}}^{-kt - k s(\tau \phi(t))}}{\phi(t)} \biggr\} \\ &=\rho \circ \tau \phi \bigl(r\bigl(T_{k}^{f}\bigr)\bigr)\end{align*}
\begin{align*}T_{1} & = \inf \{t >0 ; \;\phi(t) \,{\mathrm{e}}^{kt} W_{\tau \phi(t)} = 1 \}\\ &= \inf \biggl\{t>0 ; \; U_{s(\tau \phi(t))}= \dfrac{{\mathrm{e}}^{-kt - k s(\tau \phi(t))}}{\phi(t)} \biggr\} \\ &=\rho \circ \tau \phi \bigl(r\bigl(T_{k}^{f}\bigr)\bigr)\end{align*}
and the result follows.
Next, we introduce the following notation:
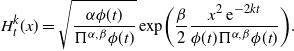 \begin{align*}H_{t}^{k}(x) = \sqrt{\dfrac{\alpha \phi(t)}{\Pi^{\alpha, \beta} \phi(t)} }\exp\biggl(\dfrac{\beta}{2} \dfrac{x^2 \,{\mathrm{e}}^{-2kt}}{\phi(t) \Pi^{\alpha, \beta} \phi(t)}\biggr).\end{align*}
\begin{align*}H_{t}^{k}(x) = \sqrt{\dfrac{\alpha \phi(t)}{\Pi^{\alpha, \beta} \phi(t)} }\exp\biggl(\dfrac{\beta}{2} \dfrac{x^2 \,{\mathrm{e}}^{-2kt}}{\phi(t) \Pi^{\alpha, \beta} \phi(t)}\biggr).\end{align*}
Our aim now is to show that the parametric families of distributions
![]() $(\mathbb{P}^{(\Pi^{\alpha, \beta} \phi,k)})_{(\alpha,\beta) \in \mathbb{R}^* \times \mathbb{R}}$
of generalised Gauss–Markov processes are related by some space–time harmonic transformations. The proof of the following proposition is similar to that of Lemma 3.2 in [Reference Alili and Patie2]. However, the proof therein has typos, so we give the full proof here.
$(\mathbb{P}^{(\Pi^{\alpha, \beta} \phi,k)})_{(\alpha,\beta) \in \mathbb{R}^* \times \mathbb{R}}$
of generalised Gauss–Markov processes are related by some space–time harmonic transformations. The proof of the following proposition is similar to that of Lemma 3.2 in [Reference Alili and Patie2]. However, the proof therein has typos, so we give the full proof here.
Proposition 5.1. For
![]() $(\alpha,\beta) \in \mathbb{R}^* \times \mathbb{R}$
and
$(\alpha,\beta) \in \mathbb{R}^* \times \mathbb{R}$
and
![]() $\phi$
as above, the process
$\phi$
as above, the process
is a
![]() $\mathbb{P}^{(\phi,k)}$
-martingale. Furthermore, the absolute-continuity relationship
$\mathbb{P}^{(\phi,k)}$
-martingale. Furthermore, the absolute-continuity relationship
holds for all
![]() $x \in \mathbb{R}$
and
$x \in \mathbb{R}$
and
![]() $t < a_{\alpha, -\beta}^{\phi}$
. Consequently, for any reals x and y, we have
$t < a_{\alpha, -\beta}^{\phi}$
. Consequently, for any reals x and y, we have
Proof. From the Itô formula, we have
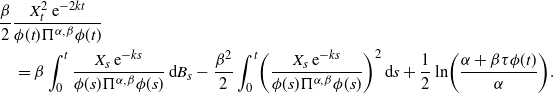 \begin{align*} &\dfrac{\beta}{2} \dfrac{X_t^2 \,{\mathrm{e}}^{-2kt}}{\phi(t) \Pi^{\alpha, \beta} \phi(t)} \\ &\quad = \beta \int_{0}^{t} \dfrac{X_s \,{\mathrm{e}}^{-ks}}{\phi(s)\Pi^{\alpha, \beta} \phi(s)} \,{\mathrm{d}} B_s - \dfrac{\beta^2}{2} \int_{0}^{t} \biggl(\dfrac{X_s \,{\mathrm{e}}^{-ks}}{\phi(s)\Pi^{\alpha, \beta} \phi(s)}\biggr)^2 \,{\mathrm{d}} s + \dfrac{1}{2} \ln \biggl(\dfrac{\alpha+ \beta \tau \phi(t)}{\alpha}\biggr).\end{align*}
\begin{align*} &\dfrac{\beta}{2} \dfrac{X_t^2 \,{\mathrm{e}}^{-2kt}}{\phi(t) \Pi^{\alpha, \beta} \phi(t)} \\ &\quad = \beta \int_{0}^{t} \dfrac{X_s \,{\mathrm{e}}^{-ks}}{\phi(s)\Pi^{\alpha, \beta} \phi(s)} \,{\mathrm{d}} B_s - \dfrac{\beta^2}{2} \int_{0}^{t} \biggl(\dfrac{X_s \,{\mathrm{e}}^{-ks}}{\phi(s)\Pi^{\alpha, \beta} \phi(s)}\biggr)^2 \,{\mathrm{d}} s + \dfrac{1}{2} \ln \biggl(\dfrac{\alpha+ \beta \tau \phi(t)}{\alpha}\biggr).\end{align*}
Now, as
![]() $\mathbb{E} [{\mathrm{e}}^{-\lambda B_t^2/2}] = (1 +\lambda t)^{-1/2}$
,
$\mathbb{E} [{\mathrm{e}}^{-\lambda B_t^2/2}] = (1 +\lambda t)^{-1/2}$
,
![]() $ \lambda > -1/t $
, we deduce that for all
$ \lambda > -1/t $
, we deduce that for all
![]() $t<a_{\alpha,-\beta}^{\phi}$
we have
$t<a_{\alpha,-\beta}^{\phi}$
we have
Hence it is a true martingale. Next, notice that
where
![]() $\langle \cdot,\cdot\rangle>$
is the quadratic variation process. Also,
$\langle \cdot,\cdot\rangle>$
is the quadratic variation process. Also,
and hence the absolute continuity relationship follows by an application of Girsanov’s theorem. Now, Doob’s optional stopping theorem implies that
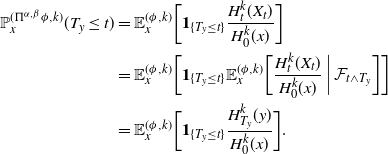 \begin{align*} \mathbb{P}^{(\Pi^{\alpha, \beta} \phi,k)}_{x} (T_y \leq t ) & = \mathbb{E}_{x}^{(\phi,k)} \biggl[\mathbf{1}_{\{T_y \leq t\}} \dfrac{H_t^{k}(X_t)}{H_0^{k}(x)}\biggr]\\ & = \mathbb{E}_{x}^{(\phi,k)} \biggl[\mathbf{1}_{\{T_y \leq t\}} \mathbb{E}_{x}^{(\phi,k)} \biggl[ \dfrac{H_t^{k}(X_t)}{H_0^{k}(x)} \biggm| \mathcal{F}_{t \wedge T_y}\biggr]\biggr] \\ & = \mathbb{E}_{x}^{(\phi,k)} \biggl[\mathbf{1}_{\{T_y \leq t\}} \dfrac{H_{T_y}^{k}(y)}{H_0^{k}(x)}\biggr].\end{align*}
\begin{align*} \mathbb{P}^{(\Pi^{\alpha, \beta} \phi,k)}_{x} (T_y \leq t ) & = \mathbb{E}_{x}^{(\phi,k)} \biggl[\mathbf{1}_{\{T_y \leq t\}} \dfrac{H_t^{k}(X_t)}{H_0^{k}(x)}\biggr]\\ & = \mathbb{E}_{x}^{(\phi,k)} \biggl[\mathbf{1}_{\{T_y \leq t\}} \mathbb{E}_{x}^{(\phi,k)} \biggl[ \dfrac{H_t^{k}(X_t)}{H_0^{k}(x)} \biggm| \mathcal{F}_{t \wedge T_y}\biggr]\biggr] \\ & = \mathbb{E}_{x}^{(\phi,k)} \biggl[\mathbf{1}_{\{T_y \leq t\}} \dfrac{H_{T_y}^{k}(y)}{H_0^{k}(x)}\biggr].\end{align*}
The result follows by differentiation.
Now we are ready to give the second proof of Theorem 3.1.
Second proof of Theorem 3.1. Let
![]() $\phi = \Sigma_{k}f$
,
$\phi = \Sigma_{k}f$
,
![]() $f_k^{\alpha,\beta} = S_{k}^{\alpha,\beta}f$
and thus, by definition,
$f_k^{\alpha,\beta} = S_{k}^{\alpha,\beta}f$
and thus, by definition,
![]() $f_k^{\alpha,\beta} = \Sigma_{k} \circ \Pi^{\alpha, -\beta} \phi$
. Since
$f_k^{\alpha,\beta} = \Sigma_{k} \circ \Pi^{\alpha, -\beta} \phi$
. Since
![]() $\Sigma_{k}$
is an involution, from Lemma 5.1 we get
$\Sigma_{k}$
is an involution, from Lemma 5.1 we get
Using identity (2) from Proposition 4.1, we get
Now, for
![]() $t < \zeta_{k, \alpha, \beta}$
, writing
$t < \zeta_{k, \alpha, \beta}$
, writing
we get
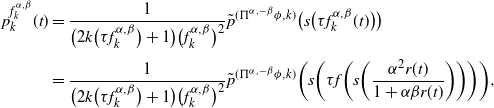 \begin{align*}p_k^{f_k^{\alpha,\beta}}(t) & = \dfrac{1}{\bigl(2k \bigl(\tau f_k^{\alpha,\beta} \bigr)+1\bigr)\bigl(f_k^{\alpha,\beta}\bigr)^2} \tilde{p}^{(\Pi^{\alpha, -\beta} \phi , k)} \bigl( s\bigl(\tau f_k^{\alpha,\beta} (t)\bigr) \bigr) \\[3pt]& = \dfrac{1}{\bigl(2k \bigl(\tau f_k^{\alpha,\beta} \bigr)+1\bigr)\bigl(f_k^{\alpha,\beta}\bigr)^2} \tilde{p}^{(\Pi^{\alpha, -\beta} \phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr),\end{align*}
\begin{align*}p_k^{f_k^{\alpha,\beta}}(t) & = \dfrac{1}{\bigl(2k \bigl(\tau f_k^{\alpha,\beta} \bigr)+1\bigr)\bigl(f_k^{\alpha,\beta}\bigr)^2} \tilde{p}^{(\Pi^{\alpha, -\beta} \phi , k)} \bigl( s\bigl(\tau f_k^{\alpha,\beta} (t)\bigr) \bigr) \\[3pt]& = \dfrac{1}{\bigl(2k \bigl(\tau f_k^{\alpha,\beta} \bigr)+1\bigr)\bigl(f_k^{\alpha,\beta}\bigr)^2} \tilde{p}^{(\Pi^{\alpha, -\beta} \phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr),\end{align*}
where we used the identity
which follows readily by a change of variable. Now, using Proposition 5.1 with the identities
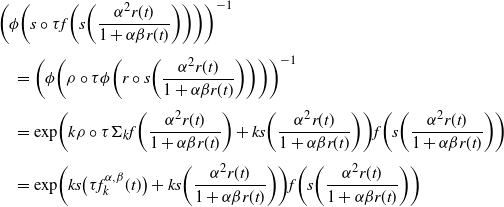 \begin{align*} & \biggl(\phi \biggl( s \circ \tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr)^{-1}\\[3pt] &\quad = \biggl(\phi \biggl(\rho \circ \tau \phi \biggl(r \circ s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr)\biggr)^{-1}\\[3pt] &\quad = \mathrm{{exp}}\biggl({k \rho \circ \tau \Sigma_{k} f \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) + k s \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)}\biggr) f \biggl(s \biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr)\\[3pt] &\quad = \mathrm{{exp}}\biggl(k s \bigl(\tau f_k^{\alpha, \beta}(t)\bigr) + k s \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)\biggr) f \biggl(s \biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr)\end{align*}
\begin{align*} & \biggl(\phi \biggl( s \circ \tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr)^{-1}\\[3pt] &\quad = \biggl(\phi \biggl(\rho \circ \tau \phi \biggl(r \circ s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr)\biggr)^{-1}\\[3pt] &\quad = \mathrm{{exp}}\biggl({k \rho \circ \tau \Sigma_{k} f \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) + k s \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)}\biggr) f \biggl(s \biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr)\\[3pt] &\quad = \mathrm{{exp}}\biggl(k s \bigl(\tau f_k^{\alpha, \beta}(t)\bigr) + k s \biggl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr)\biggr) f \biggl(s \biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr)\end{align*}
and
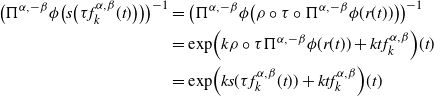 \begin{align*} \bigl(\Pi^{\alpha, - \beta} \phi\bigl( s \bigl(\tau f_k^{\alpha, \beta}(t)\bigr)\bigr)\bigr)^{-1} & = \bigl(\Pi^{\alpha, - \beta} \phi\bigl( \rho \circ \tau \circ \Pi^{\alpha, -\beta} \phi (r(t)) \bigr)\bigr)^{-1} \\ &= \exp \Bigl({k \rho \circ \tau \Pi^{\alpha, -\beta} \phi (r(t)) + kt} f_k^{\alpha, \beta}\Bigr) (t) \\ & = \exp \Bigl({k s (\tau f_k^{\alpha, \beta}(t)) + kt} f_k^{\alpha, \beta}\Bigr) (t) \end{align*}
\begin{align*} \bigl(\Pi^{\alpha, - \beta} \phi\bigl( s \bigl(\tau f_k^{\alpha, \beta}(t)\bigr)\bigr)\bigr)^{-1} & = \bigl(\Pi^{\alpha, - \beta} \phi\bigl( \rho \circ \tau \circ \Pi^{\alpha, -\beta} \phi (r(t)) \bigr)\bigr)^{-1} \\ &= \exp \Bigl({k \rho \circ \tau \Pi^{\alpha, -\beta} \phi (r(t)) + kt} f_k^{\alpha, \beta}\Bigr) (t) \\ & = \exp \Bigl({k s (\tau f_k^{\alpha, \beta}(t)) + kt} f_k^{\alpha, \beta}\Bigr) (t) \end{align*}
yields, for any
![]() $t < \zeta_{k, \alpha, \beta}$
,
$t < \zeta_{k, \alpha, \beta}$
,
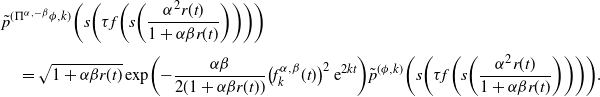 \begin{align*} & \tilde{p}^{(\Pi^{\alpha, -\beta} \phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr) \\[3pt]& \quad = \sqrt{1+ \alpha \beta r(t)} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(f_k^{\alpha,\beta}(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) \tilde{p}^{(\phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr).\end{align*}
\begin{align*} & \tilde{p}^{(\Pi^{\alpha, -\beta} \phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr) \\[3pt]& \quad = \sqrt{1+ \alpha \beta r(t)} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(f_k^{\alpha,\beta}(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\biggr) \tilde{p}^{(\phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr).\end{align*}
Hence
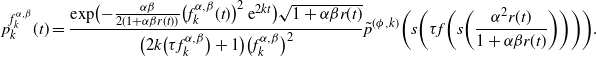 \begin{align*} p_k^{f_k^{\alpha,\beta}}(t) = \dfrac{\mathrm{{exp}}\bigl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(f_k^{\alpha,\beta}(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\bigr)\sqrt{1+ \alpha \beta r(t)}}{\bigl(2k \bigl(\tau f_k^{\alpha,\beta} \bigr)+1\bigr)\bigl(f_k^{\alpha,\beta}\bigr)^2} \tilde{p}^{(\phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr).\end{align*}
\begin{align*} p_k^{f_k^{\alpha,\beta}}(t) = \dfrac{\mathrm{{exp}}\bigl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl(f_k^{\alpha,\beta}(t)\bigr)^2 \,{\mathrm{e}}^{2kt}}\bigr)\sqrt{1+ \alpha \beta r(t)}}{\bigl(2k \bigl(\tau f_k^{\alpha,\beta} \bigr)+1\bigr)\bigl(f_k^{\alpha,\beta}\bigr)^2} \tilde{p}^{(\phi , k)} \biggl( s \biggl(\tau f \biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \biggr) \biggr).\end{align*}
5.3. Third proof of Theorem 3.1 via the Lie group symmetries
We now provide the last proof for Theorem 3.1 using the Lie group symmetries approach. For Lie group theory, we refer to [Reference Bluman and Cole9, Reference Olver29]. In general, this technique can be used to find solutions to differential equations with new boundary conditions from known ones. For example, the Lie point symmetries of the heat equation
can be found in [Reference Alili and Patie2, Section 3.3]. Before going through the proof, we first discuss the connections between the boundary value problem (5.5) corresponding to the heat equation and the OU Fokker–Planck equation. Set
We introduce the following boundary value problem:
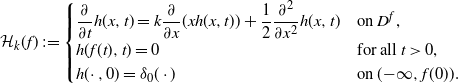 \begin{equation}\mathcal{H}_k(f) \;:\!= \begin{cases} \dfrac{\partial}{\partial t}h(x,t)= k \dfrac{\partial}{\partial x}(x h(x,t)) +\dfrac{1}{2}\dfrac{\partial^2}{\partial x^2}h(x,t) & \text{on $ D^f$,}\\ h(f(t),t)=0 &\text{for all $ t>0$,} \\ h(\cdot\,,0) = \delta_0(\cdot) & \text{on $ ({-}\infty,f(0))$.} \end{cases}\end{equation}
\begin{equation}\mathcal{H}_k(f) \;:\!= \begin{cases} \dfrac{\partial}{\partial t}h(x,t)= k \dfrac{\partial}{\partial x}(x h(x,t)) +\dfrac{1}{2}\dfrac{\partial^2}{\partial x^2}h(x,t) & \text{on $ D^f$,}\\ h(f(t),t)=0 &\text{for all $ t>0$,} \\ h(\cdot\,,0) = \delta_0(\cdot) & \text{on $ ({-}\infty,f(0))$.} \end{cases}\end{equation}
Note that the first equation in
![]() $\mathcal{H}_k(f)$
is the OU Fokker–Planck equation (1.3). As
$\mathcal{H}_k(f)$
is the OU Fokker–Planck equation (1.3). As
![]() $k \to 0$
, we recover the heat equation and obtain the corresponding boundary value problem for the BM
$k \to 0$
, we recover the heat equation and obtain the corresponding boundary value problem for the BM
![]() $\mathcal{H}(f)$
. By Proposition 5.4.3.1 of [Reference Jeanblanc, Yor and Chesney21], solutions to
$\mathcal{H}(f)$
. By Proposition 5.4.3.1 of [Reference Jeanblanc, Yor and Chesney21], solutions to
![]() $\mathcal{H}(f)$
and
$\mathcal{H}(f)$
and
![]() $\mathcal{H}_k(f)$
admit the following probabilistic representations:
$\mathcal{H}_k(f)$
admit the following probabilistic representations:
Using (1.1) and (5.1), we connect the two solutions directly in the following way:
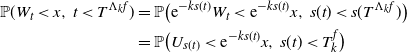 \begin{align*} \mathbb{P}(W_t < x, \; t< T^{\Lambda_{k} f}) &= \mathbb{P}\bigl({\mathrm{e}}^{-ks(t)} W_{t} < {\mathrm{e}}^{-ks(t)} x , \; s(t) < s(T^{\Lambda_{k} f})\bigr) \\ &= \mathbb{P}\bigl(U_{s(t)} < {\mathrm{e}}^{-ks(t)}x, \; s(t) < T^{f}_k\bigr)\end{align*}
\begin{align*} \mathbb{P}(W_t < x, \; t< T^{\Lambda_{k} f}) &= \mathbb{P}\bigl({\mathrm{e}}^{-ks(t)} W_{t} < {\mathrm{e}}^{-ks(t)} x , \; s(t) < s(T^{\Lambda_{k} f})\bigr) \\ &= \mathbb{P}\bigl(U_{s(t)} < {\mathrm{e}}^{-ks(t)}x, \; s(t) < T^{f}_k\bigr)\end{align*}
and so
where h now denotes a solution to
![]() $\mathcal{H}(\Lambda_{k} f)$
. This shows that the solutions to the Fokker–Planck equation of the OU on
$\mathcal{H}(\Lambda_{k} f)$
. This shows that the solutions to the Fokker–Planck equation of the OU on
![]() $D^f$
are directly connected to the solutions to the heat equation on
$D^f$
are directly connected to the solutions to the heat equation on
![]() $D^{\Lambda_{k} f}$
. As will become clear in the third proof of Theorem 3.1 at the end of this section, the aim is to find a solution to the Fokker–Planck equation of the OU such that it vanishes on our desired transformed boundary
$D^{\Lambda_{k} f}$
. As will become clear in the third proof of Theorem 3.1 at the end of this section, the aim is to find a solution to the Fokker–Planck equation of the OU such that it vanishes on our desired transformed boundary
![]() $S_{k}^{\alpha,\beta}f$
. To do this, we first present a proposition for the OU which resembles Proposition 3.5 in [Reference Alili and Patie2] for the Brownian motion.
$S_{k}^{\alpha,\beta}f$
. To do this, we first present a proposition for the OU which resembles Proposition 3.5 in [Reference Alili and Patie2] for the Brownian motion.
Proposition 5.2. Let
![]() $h_k$
be the solution to the boundary value problem
$h_k$
be the solution to the boundary value problem
![]() $\mathcal{H}_k(f)$
in (5.5). Then, for any
$\mathcal{H}_k(f)$
in (5.5). Then, for any
![]() $\alpha>0$
,
$\alpha>0$
,
![]() $\beta \in \mathbb{R}$
, the mapping
$\beta \in \mathbb{R}$
, the mapping
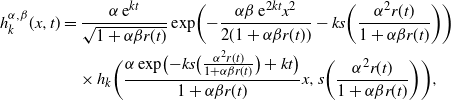 \begin{align} h^{\alpha,\beta}_k(x,t) & = \dfrac{\alpha \,{\mathrm{e}}^{kt}}{\sqrt{1+\alpha \beta r(t)}} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta \,{\mathrm{e}}^{2kt} x^2}{2(1+ \alpha \beta r(t))} - k s\biggl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr)}\biggr) \notag \\ &\quad \times h_{k}\biggl(\dfrac{\alpha \,\mathrm{{exp}}\bigl({-k s\bigl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\bigr)+kt}\bigr)}{1+\alpha \beta r(t)} x, s\biggl(\dfrac{\alpha^2 r(t)}{1+\alpha \beta r(t)} \biggr) \biggr), \end{align}
\begin{align} h^{\alpha,\beta}_k(x,t) & = \dfrac{\alpha \,{\mathrm{e}}^{kt}}{\sqrt{1+\alpha \beta r(t)}} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta \,{\mathrm{e}}^{2kt} x^2}{2(1+ \alpha \beta r(t))} - k s\biggl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr)}\biggr) \notag \\ &\quad \times h_{k}\biggl(\dfrac{\alpha \,\mathrm{{exp}}\bigl({-k s\bigl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\bigr)+kt}\bigr)}{1+\alpha \beta r(t)} x, s\biggl(\dfrac{\alpha^2 r(t)}{1+\alpha \beta r(t)} \biggr) \biggr), \end{align}
for
![]() $t < \zeta_{k, \alpha, \beta}$
, is the solution to the boundary value problem
$t < \zeta_{k, \alpha, \beta}$
, is the solution to the boundary value problem
![]() $\mathcal{H}_k\bigl(S_{k}^{\alpha,\beta}f\bigr)$
.
$\mathcal{H}_k\bigl(S_{k}^{\alpha,\beta}f\bigr)$
.
Proof. Firstly, if f is an infinitely continuously differentiable function, then so is its transformation
![]() $S_{k}^{\alpha,\beta}f$
. From Proposition 3.5 in [Reference Alili and Patie2], the function
$S_{k}^{\alpha,\beta}f$
. From Proposition 3.5 in [Reference Alili and Patie2], the function
is a solution to
![]() $\mathcal{H}(S^{\alpha,\beta} \Lambda_{k} f)$
whenever h solves
$\mathcal{H}(S^{\alpha,\beta} \Lambda_{k} f)$
whenever h solves
![]() $\mathcal{H}(\Lambda_{k} f)$
. Now, using relation (5.7), we define
$\mathcal{H}(\Lambda_{k} f)$
. Now, using relation (5.7), we define
![]() $\tilde{h}^{\alpha,\beta}$
as
$\tilde{h}^{\alpha,\beta}$
as
![]() $\tilde{h}^{\alpha,\beta}= {\mathrm{e}}^{kt} h^{\alpha,\beta}({\mathrm{e}}^{kt}x, r(t)) $
. Then this expression is a solution to the boundary value problem
$\tilde{h}^{\alpha,\beta}= {\mathrm{e}}^{kt} h^{\alpha,\beta}({\mathrm{e}}^{kt}x, r(t)) $
. Then this expression is a solution to the boundary value problem
![]() $\mathcal{H}_k(S_{k}^{\alpha,\beta}f)$
. Using relation (5.7) again, we can write
$\mathcal{H}_k(S_{k}^{\alpha,\beta}f)$
. Using relation (5.7) again, we can write
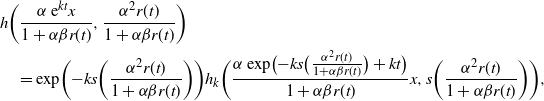 \begin{align*}&h\biggl(\dfrac{\alpha \,{\mathrm{e}}^{kt} x}{1+\alpha \beta r(t)}, \dfrac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr) \\ &\quad = \mathrm{{exp}}\biggl({ -ks\biggl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr)}\biggr) h_k\biggl(\dfrac{\alpha \,\mathrm{{exp}}\bigl({-k s\bigl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\bigr)+kt}\bigr)}{1+\alpha \beta r(t)} x, s\biggl(\dfrac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr) \biggr),\end{align*}
\begin{align*}&h\biggl(\dfrac{\alpha \,{\mathrm{e}}^{kt} x}{1+\alpha \beta r(t)}, \dfrac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr) \\ &\quad = \mathrm{{exp}}\biggl({ -ks\biggl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr)}\biggr) h_k\biggl(\dfrac{\alpha \,\mathrm{{exp}}\bigl({-k s\bigl(\frac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\bigr)+kt}\bigr)}{1+\alpha \beta r(t)} x, s\biggl(\dfrac{\alpha^2 r(t)}{1+\alpha \beta r(t)}\biggr) \biggr),\end{align*}
and thus we find that
![]() $\tilde{h}^{\alpha,\beta}$
and
$\tilde{h}^{\alpha,\beta}$
and
![]() $h_{k}^{\alpha,\beta}$
coincide, which implies that
$h_{k}^{\alpha,\beta}$
coincide, which implies that
![]() $h_{k}^{\alpha,\beta}$
is indeed a solution to
$h_{k}^{\alpha,\beta}$
is indeed a solution to
![]() $\mathcal{H}_k\bigl(S_{k}^{\alpha,\beta}f\bigr)$
. Moreover, we obtain
$\mathcal{H}_k\bigl(S_{k}^{\alpha,\beta}f\bigr)$
. Moreover, we obtain
![]() $h_{k}^{\alpha,\beta}(x,t) = 0 \iff x = S_{k}^{\alpha, \beta}f(t)$
, because by assumption
$h_{k}^{\alpha,\beta}(x,t) = 0 \iff x = S_{k}^{\alpha, \beta}f(t)$
, because by assumption
![]() $h_{k}$
is a solution to
$h_{k}$
is a solution to
![]() $\mathcal{H}_k(f)$
, hence
$\mathcal{H}_k(f)$
, hence
![]() $h_k(f(\cdot),\cdot)=0$
. Also,
$h_k(f(\cdot),\cdot)=0$
. Also,
Now let us investigate
![]() $h_{k}^{\alpha,0}$
. Using relation (5.7) again, we get
$h_{k}^{\alpha,0}$
. Using relation (5.7) again, we get
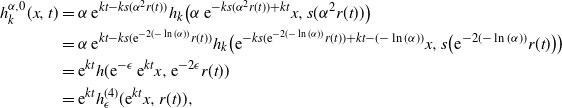 \begin{align*}h_{k}^{\alpha,0}(x,t) & = \alpha \,{\mathrm{e}}^{kt -ks(\alpha^2 r(t))} h_{k}\bigl(\alpha \,{\mathrm{e}}^{-ks(\alpha^2 r(t))+kt}x, s(\alpha^2 r(t))\bigr) \\& = \alpha \,{\mathrm{e}}^{kt -ks({\mathrm{e}}^{-2({-}\ln(\alpha))} r(t))} h_{k}\bigl({\mathrm{e}}^{-ks({\mathrm{e}}^{-2({-}\ln(\alpha))} r(t))+kt - ({-}\ln(\alpha))}x, s \bigl({\mathrm{e}}^{-2({-}\ln(\alpha))} r(t)\bigr)\bigr) \\& = {\mathrm{e}}^{kt} h({\mathrm{e}}^{-\epsilon} \,{\mathrm{e}}^{kt} x, {\mathrm{e}}^{-2\epsilon} r(t))\\& = {\mathrm{e}}^{kt} h^{(4)}_{\epsilon}({\mathrm{e}}^{kt}x, r(t)),\end{align*}
\begin{align*}h_{k}^{\alpha,0}(x,t) & = \alpha \,{\mathrm{e}}^{kt -ks(\alpha^2 r(t))} h_{k}\bigl(\alpha \,{\mathrm{e}}^{-ks(\alpha^2 r(t))+kt}x, s(\alpha^2 r(t))\bigr) \\& = \alpha \,{\mathrm{e}}^{kt -ks({\mathrm{e}}^{-2({-}\ln(\alpha))} r(t))} h_{k}\bigl({\mathrm{e}}^{-ks({\mathrm{e}}^{-2({-}\ln(\alpha))} r(t))+kt - ({-}\ln(\alpha))}x, s \bigl({\mathrm{e}}^{-2({-}\ln(\alpha))} r(t)\bigr)\bigr) \\& = {\mathrm{e}}^{kt} h({\mathrm{e}}^{-\epsilon} \,{\mathrm{e}}^{kt} x, {\mathrm{e}}^{-2\epsilon} r(t))\\& = {\mathrm{e}}^{kt} h^{(4)}_{\epsilon}({\mathrm{e}}^{kt}x, r(t)),\end{align*}
where
![]() $\epsilon=-\ln(\alpha)$
. Now, the latter
$\epsilon=-\ln(\alpha)$
. Now, the latter
![]() $h^{(4)}_{\epsilon}$
is the fourth symmetry of the heat equation listed in [Reference Alili and Patie2, Section 3.3], meaning that it satisfies the heat equation. By using relation (5.7), we see that
$h^{(4)}_{\epsilon}$
is the fourth symmetry of the heat equation listed in [Reference Alili and Patie2, Section 3.3], meaning that it satisfies the heat equation. By using relation (5.7), we see that
![]() ${\mathrm{e}}^{kt} h^{(4)}_{\epsilon}({\mathrm{e}}^{kt}x, r(t))$
indeed satisfies the Fokker–Planck equation of the OU, so
${\mathrm{e}}^{kt} h^{(4)}_{\epsilon}({\mathrm{e}}^{kt}x, r(t))$
indeed satisfies the Fokker–Planck equation of the OU, so
![]() $h_{k}^{\alpha,0}$
is a solution to
$h_{k}^{\alpha,0}$
is a solution to
![]() $\mathcal{H}_{k}(S_{k}^{\alpha,0}f)$
and thus in particular
$\mathcal{H}_{k}(S_{k}^{\alpha,0}f)$
and thus in particular
![]() $h_{k}^{\alpha,0}(\cdot,0) = \delta_{0}(\cdot)$
on
$h_{k}^{\alpha,0}(\cdot,0) = \delta_{0}(\cdot)$
on
![]() $({-}\infty, {{f(0)}/{\alpha}})$
. Hence we get
$({-}\infty, {{f(0)}/{\alpha}})$
. Hence we get
which concludes the proof.
5.3.1. Lie symmetries of OU Fokker–Planck equation
In this section, we provide a direct construction of the function
![]() $h_{k}^{\alpha, \beta}$
given in (5.8) from the Lie symmetries of the OU Fokker–Planck equation (1.3). Using techniques similar to those discussed in [Reference Olver29, Section 2.4], after some lengthy and tedious calculations, we find that the Lie algebra of infinitesimal symmetries of the OU Fokker–Planck equation is spanned by six vector fields, where x, t are the two independent variables and h is the dependent variable,
$h_{k}^{\alpha, \beta}$
given in (5.8) from the Lie symmetries of the OU Fokker–Planck equation (1.3). Using techniques similar to those discussed in [Reference Olver29, Section 2.4], after some lengthy and tedious calculations, we find that the Lie algebra of infinitesimal symmetries of the OU Fokker–Planck equation is spanned by six vector fields, where x, t are the two independent variables and h is the dependent variable,
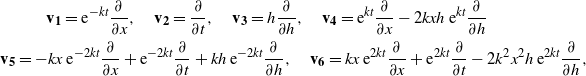 \begin{align*}\mathbf{v}_{\mathbf{1}} = {\mathrm{e}}^{-kt} \dfrac{\partial}{\partial x}, \quad \mathbf{v}_{\mathbf{2}} = \dfrac{\partial}{\partial t}, \quad \mathbf{v}_{\mathbf{3}} = h \dfrac{\partial }{\partial h}, \quad\mathbf{v}_{\mathbf{4}} = {\mathrm{e}}^{kt} \dfrac{\partial }{\partial x} - 2kxh \,{\mathrm{e}}^{kt} \dfrac{\partial }{\partial h}\qquad\qquad\qquad\\\mathbf{v}_{\mathbf{5}} = -kx \,{\mathrm{e}}^{-2kt}\dfrac{\partial }{\partial x} + {\mathrm{e}}^{-2kt}\dfrac{\partial }{\partial t}+ kh \,{\mathrm{e}}^{-2kt} \dfrac{\partial }{\partial h}, \quad\mathbf{v}_{\mathbf{6}} = kx \,{\mathrm{e}}^{2kt}\dfrac{\partial }{\partial x} + {\mathrm{e}}^{2kt}\dfrac{\partial }{\partial t} - 2k^2 x^2 h \,{\mathrm{e}}^{2kt} \dfrac{\partial }{\partial h},\end{align*}
\begin{align*}\mathbf{v}_{\mathbf{1}} = {\mathrm{e}}^{-kt} \dfrac{\partial}{\partial x}, \quad \mathbf{v}_{\mathbf{2}} = \dfrac{\partial}{\partial t}, \quad \mathbf{v}_{\mathbf{3}} = h \dfrac{\partial }{\partial h}, \quad\mathbf{v}_{\mathbf{4}} = {\mathrm{e}}^{kt} \dfrac{\partial }{\partial x} - 2kxh \,{\mathrm{e}}^{kt} \dfrac{\partial }{\partial h}\qquad\qquad\qquad\\\mathbf{v}_{\mathbf{5}} = -kx \,{\mathrm{e}}^{-2kt}\dfrac{\partial }{\partial x} + {\mathrm{e}}^{-2kt}\dfrac{\partial }{\partial t}+ kh \,{\mathrm{e}}^{-2kt} \dfrac{\partial }{\partial h}, \quad\mathbf{v}_{\mathbf{6}} = kx \,{\mathrm{e}}^{2kt}\dfrac{\partial }{\partial x} + {\mathrm{e}}^{2kt}\dfrac{\partial }{\partial t} - 2k^2 x^2 h \,{\mathrm{e}}^{2kt} \dfrac{\partial }{\partial h},\end{align*}
and by the infinite-dimensional sub-algebra
![]() $\mathbf{v}_{\boldsymbol\alpha} = u(x,t){{\partial }/{\partial h}}$
, where u(x,t) is an arbitrary solution of the OU Fokker–Planck equation. Now, by exponentiating the basis, as in [Reference Olver29, page 89], we can produce the one-parameter group of transformations leaving invariant
$\mathbf{v}_{\boldsymbol\alpha} = u(x,t){{\partial }/{\partial h}}$
, where u(x,t) is an arbitrary solution of the OU Fokker–Planck equation. Now, by exponentiating the basis, as in [Reference Olver29, page 89], we can produce the one-parameter group of transformations leaving invariant
![]() $\mathcal{H}_{k}(f)$
. Doing this procedure for each of the vectors fields, we obtain the one-parameter groups
$\mathcal{H}_{k}(f)$
. Doing this procedure for each of the vectors fields, we obtain the one-parameter groups
![]() $G_i$
generated by the
$G_i$
generated by the
![]() $\mathbf{v}_{\mathbf{i}}$
. Since each group
$\mathbf{v}_{\mathbf{i}}$
. Since each group
![]() $G_i$
is a symmetry group, if h is a solution to (1.3), then the following are also solutions to (1.3):
$G_i$
is a symmetry group, if h is a solution to (1.3), then the following are also solutions to (1.3):
 \begin{equation} \begin{aligned} h^{(1)}_{k,\epsilon}(x,t) &=h(x- \epsilon \,{\mathrm{e}}^{-kt}, t ), \\h^{(2)}_{k,\epsilon}(x,t) &=h(x, t- \epsilon ), \\ h^{(3)}_{k,\epsilon}(x,t) &={\mathrm{e}}^{\epsilon} h(x, t ), \\ h^{(4)}_{k,\epsilon}(x,t) &={\mathrm{e}}^{-2kx \epsilon \,{\mathrm{e}}^{kt}+k \epsilon^2 \,{\mathrm{e}}^{2kt}}h(x- \epsilon \,{\mathrm{e}}^{kt}, t ), \\ h^{(5)}_{k,\epsilon}(x,t) &=\dfrac{{\mathrm{e}}^{kt}}{\sqrt{{\mathrm{e}}^{2kt} - 2k\epsilon}} h\biggl(\dfrac{x \,{\mathrm{e}}^{kt}}{\sqrt{{\mathrm{e}}^{2kt} - 2k\epsilon}}, \dfrac{\ln{({\mathrm{e}}^{2kt}-2k\epsilon)}}{2k} \biggr), \\ h^{(6)}_{k,\epsilon}(x,t) &=\mathrm{{exp}}\biggl({\frac{-2k^2 x^2 \epsilon}{{\mathrm{e}}^{-2kt} + 2k\epsilon}}\biggr) h\biggl(\dfrac{x \,{\mathrm{e}}^{-kt}}{\sqrt{{\mathrm{e}}^{-2kt} + 2k\epsilon}}, \dfrac{\ln{({\mathrm{e}}^{-2kt}+2k\epsilon)}}{-2k} \biggr). \end{aligned} \end{equation}
\begin{equation} \begin{aligned} h^{(1)}_{k,\epsilon}(x,t) &=h(x- \epsilon \,{\mathrm{e}}^{-kt}, t ), \\h^{(2)}_{k,\epsilon}(x,t) &=h(x, t- \epsilon ), \\ h^{(3)}_{k,\epsilon}(x,t) &={\mathrm{e}}^{\epsilon} h(x, t ), \\ h^{(4)}_{k,\epsilon}(x,t) &={\mathrm{e}}^{-2kx \epsilon \,{\mathrm{e}}^{kt}+k \epsilon^2 \,{\mathrm{e}}^{2kt}}h(x- \epsilon \,{\mathrm{e}}^{kt}, t ), \\ h^{(5)}_{k,\epsilon}(x,t) &=\dfrac{{\mathrm{e}}^{kt}}{\sqrt{{\mathrm{e}}^{2kt} - 2k\epsilon}} h\biggl(\dfrac{x \,{\mathrm{e}}^{kt}}{\sqrt{{\mathrm{e}}^{2kt} - 2k\epsilon}}, \dfrac{\ln{({\mathrm{e}}^{2kt}-2k\epsilon)}}{2k} \biggr), \\ h^{(6)}_{k,\epsilon}(x,t) &=\mathrm{{exp}}\biggl({\frac{-2k^2 x^2 \epsilon}{{\mathrm{e}}^{-2kt} + 2k\epsilon}}\biggr) h\biggl(\dfrac{x \,{\mathrm{e}}^{-kt}}{\sqrt{{\mathrm{e}}^{-2kt} + 2k\epsilon}}, \dfrac{\ln{({\mathrm{e}}^{-2kt}+2k\epsilon)}}{-2k} \biggr). \end{aligned} \end{equation}
Notice that these symmetry groups provide an explanation of the invariance of the law of the OU process under some specific transformations. More precisely,
![]() $ h^{(1)}_{k,\epsilon}$
and
$ h^{(1)}_{k,\epsilon}$
and
![]() $ h^{(2)}_{k,\epsilon}$
, respectively, show the space and time invariance of the law of the OU,
$ h^{(2)}_{k,\epsilon}$
, respectively, show the space and time invariance of the law of the OU,
![]() $ h^{(3)}_{k,\epsilon}$
is the trivial multiplication by a constant,
$ h^{(3)}_{k,\epsilon}$
is the trivial multiplication by a constant,
![]() $ h^{(4)}_{k,\epsilon}$
represents the Girsanov transform connecting the law of the OU with different exponential drifts, while compositions of
$ h^{(4)}_{k,\epsilon}$
represents the Girsanov transform connecting the law of the OU with different exponential drifts, while compositions of
![]() $ h^{(5)}_{k,\epsilon}$
and
$ h^{(5)}_{k,\epsilon}$
and
![]() $ h^{(6)}_{k,\epsilon}$
are deeply connected to the change of measure connecting the law of the OU with its bridges.
$ h^{(6)}_{k,\epsilon}$
are deeply connected to the change of measure connecting the law of the OU with its bridges.
In Proposition 5.2 we proved that the function
![]() $h_{k}^{\alpha,\beta}$
is a solution to the boundary value problem
$h_{k}^{\alpha,\beta}$
is a solution to the boundary value problem
![]() $\mathcal{H}_{k}(S_{k}^{\alpha,\beta}f)$
by directly using the relation between the two boundary value problems in (5.5). We can also construct this function directly using the symmetries above.
$\mathcal{H}_{k}(S_{k}^{\alpha,\beta}f)$
by directly using the relation between the two boundary value problems in (5.5). We can also construct this function directly using the symmetries above.
Remark 5.1. Proposition 5 of [Reference Muravey27] gives a general class of symmetries for SDEs with a drift term specified in Proposition 4 therein. The expression therein contains misprints in
![]() $P^{\epsilon}_{1,2}$
and
$P^{\epsilon}_{1,2}$
and
![]() $\mathcal{T}_{p_{1,2}}$
. Using the notation in the original article, the correct expressions are
$\mathcal{T}_{p_{1,2}}$
. Using the notation in the original article, the correct expressions are
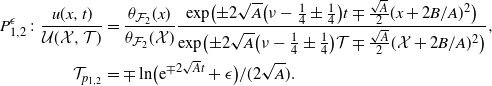 \begin{align*}P^{\epsilon}_{1,2} \colon \dfrac{u(x,t)}{\mathcal{U}(\mathcal{X},\mathcal{T})} & = \dfrac{\theta_{\mathcal{F}_2}(x)}{\theta_{\mathcal{F}_2}(\mathcal{X})} \dfrac{\mathrm{{exp}}\bigl({\pm 2 \sqrt{A} \bigl(\nu - \frac{1}{4} \pm \frac{1}{4} \bigr)t \mp \frac{\sqrt{A}}{2} (x+ 2B/A)^2 }\bigr)}{\mathrm{{exp}}\bigl({\pm 2 \sqrt{A} \bigl(\nu - \frac{1}{4} \pm \frac{1}{4} \bigr)\mathcal{T} \mp \frac{\sqrt{A}}{2} (\mathcal{X}+ 2B/A)^2}\bigr)},\\\mathcal{T}_{p_{1,2}} & = \mp \ln \bigl({\mathrm{e}}^{\mp 2\sqrt{A}t} + \epsilon\bigr)/(2\sqrt{A}).\end{align*}
\begin{align*}P^{\epsilon}_{1,2} \colon \dfrac{u(x,t)}{\mathcal{U}(\mathcal{X},\mathcal{T})} & = \dfrac{\theta_{\mathcal{F}_2}(x)}{\theta_{\mathcal{F}_2}(\mathcal{X})} \dfrac{\mathrm{{exp}}\bigl({\pm 2 \sqrt{A} \bigl(\nu - \frac{1}{4} \pm \frac{1}{4} \bigr)t \mp \frac{\sqrt{A}}{2} (x+ 2B/A)^2 }\bigr)}{\mathrm{{exp}}\bigl({\pm 2 \sqrt{A} \bigl(\nu - \frac{1}{4} \pm \frac{1}{4} \bigr)\mathcal{T} \mp \frac{\sqrt{A}}{2} (\mathcal{X}+ 2B/A)^2}\bigr)},\\\mathcal{T}_{p_{1,2}} & = \mp \ln \bigl({\mathrm{e}}^{\mp 2\sqrt{A}t} + \epsilon\bigr)/(2\sqrt{A}).\end{align*}
If we set
![]() $A= k^2, B=0, \nu=0$
and
$A= k^2, B=0, \nu=0$
and
![]() $\theta_{\mathcal{F}_2}(x)= {\mathrm{e}}^{-kx^2/2}$
, we recover the above symmetries (5.9) for the OU process.
$\theta_{\mathcal{F}_2}(x)= {\mathrm{e}}^{-kx^2/2}$
, we recover the above symmetries (5.9) for the OU process.
Lemma 5.2.
Although the calculation is tedious, it can be easily shown that the expression given in Lemma 5.2 holds. Now, because the function
![]() $h_{k}^{\alpha,\beta}$
is a composition of symmetries of the OU Fokker–Planck equation, then it is itself a solution to the OU Fokker–Planck equation. Lemma 5.2 can then be used to shorten the first part of the proof given in Proposition 5.2. Now we give the third proof of Theorem 3.1.
$h_{k}^{\alpha,\beta}$
is a composition of symmetries of the OU Fokker–Planck equation, then it is itself a solution to the OU Fokker–Planck equation. Lemma 5.2 can then be used to shorten the first part of the proof given in Proposition 5.2. Now we give the third proof of Theorem 3.1.
Third proof of Theorem 3.1. Let
![]() $h_k$
be the solution to
$h_k$
be the solution to
![]() $\mathcal{H}_{k}(f)$
. Then, by (5.6), we have
$\mathcal{H}_{k}(f)$
. Then, by (5.6), we have
Setting
![]() $p_k^{f}(t) \,{\mathrm{d}} t = \mathbb{P}\bigl( T_{k}^{f} \in {\mathrm{d}} t \bigr) $
, we get
$p_k^{f}(t) \,{\mathrm{d}} t = \mathbb{P}\bigl( T_{k}^{f} \in {\mathrm{d}} t \bigr) $
, we get
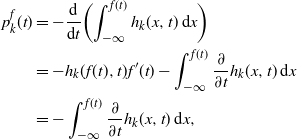 \begin{align*} p_k^{f}(t) &= - \dfrac{{\mathrm{d}}}{{\mathrm{d}} t} \biggl(\int_{-\infty}^{f(t)} h_{k}(x,t) \,{\mathrm{d}} x \biggr) \\ & = -h_{k}(f(t),t) f^{\prime}(t) - \int_{-\infty}^{f(t)} \dfrac{\partial }{\partial t} h_{k}(x,t) \,{\mathrm{d}} x \\ &= - \int_{-\infty}^{f(t)} \dfrac{\partial }{\partial t} h_{k}(x,t) \,{\mathrm{d}} x,\end{align*}
\begin{align*} p_k^{f}(t) &= - \dfrac{{\mathrm{d}}}{{\mathrm{d}} t} \biggl(\int_{-\infty}^{f(t)} h_{k}(x,t) \,{\mathrm{d}} x \biggr) \\ & = -h_{k}(f(t),t) f^{\prime}(t) - \int_{-\infty}^{f(t)} \dfrac{\partial }{\partial t} h_{k}(x,t) \,{\mathrm{d}} x \\ &= - \int_{-\infty}^{f(t)} \dfrac{\partial }{\partial t} h_{k}(x,t) \,{\mathrm{d}} x,\end{align*}
because
![]() $h_{k}$
vanishes on the boundary f. Using the OU Fokker–Planck equation (1.3), we get
$h_{k}$
vanishes on the boundary f. Using the OU Fokker–Planck equation (1.3), we get
Now, by Proposition 5.2 and Lemma 5.2, we deduce that
![]() $h_{k}^{\alpha,\beta}$
in (5.8) is a solution to the boundary value problem
$h_{k}^{\alpha,\beta}$
in (5.8) is a solution to the boundary value problem
![]() $\mathcal{H}_{k}\bigl(S_{k}^{\alpha,\beta}f\bigr)$
. Hence, using
$\mathcal{H}_{k}\bigl(S_{k}^{\alpha,\beta}f\bigr)$
. Hence, using
![]() $h_{k}^{\alpha,\beta}$
with its corresponding boundary
$h_{k}^{\alpha,\beta}$
with its corresponding boundary
![]() $S_{k}^{\alpha,\beta}f$
in (5.10) gives us expression (3.1) from Theorem 3.1.
$S_{k}^{\alpha,\beta}f$
in (5.10) gives us expression (3.1) from Theorem 3.1.
Remark 5.2. The algebraic proof based on the Lie symmetry approach yields uniqueness of the family of transformations
![]() $S_{k}^{\alpha,\beta}$
and thus of the relationship (3.1). Indeed, the function
$S_{k}^{\alpha,\beta}$
and thus of the relationship (3.1). Indeed, the function
![]() $h_{k}^{\alpha,\beta}$
is the unique solution to
$h_{k}^{\alpha,\beta}$
is the unique solution to
![]() $\mathcal{H}_{k}\bigl(S_{k}^{\alpha, \beta} f\bigr)$
, and in order to satisfy the corresponding third condition of (5.5), we can only construct further solutions by composing it with symmetry groups (5.9) such that the time component is 0 whenever
$\mathcal{H}_{k}\bigl(S_{k}^{\alpha, \beta} f\bigr)$
, and in order to satisfy the corresponding third condition of (5.5), we can only construct further solutions by composing it with symmetry groups (5.9) such that the time component is 0 whenever
![]() $t=0$
. This only leads to a change in constants
$t=0$
. This only leads to a change in constants
![]() $\alpha$
or
$\alpha$
or
![]() $\beta$
, making
$\beta$
, making
![]() $S_{k}^{\alpha,\beta}$
the only non-trivial transformation leading to (3.1). Note that one could use symmetry
$S_{k}^{\alpha,\beta}$
the only non-trivial transformation leading to (3.1). Note that one could use symmetry
![]() $h^{(4)}_{k, \epsilon}$
to add an extra trend to the
$h^{(4)}_{k, \epsilon}$
to add an extra trend to the
![]() $S_{k}^{\alpha,\beta}$
transformation, but the form of the transformation would stay the same.
$S_{k}^{\alpha,\beta}$
transformation, but the form of the transformation would stay the same.
Remark 5.3. When we take the limit as k goes to 0 of the symmetries in (5.9), we only recover the first three symmetries of the heat equation, found in [Reference Alili and Patie2, Section 3.3]. The rest of the symmetries of the heat equation can be recovered by using a combination of the symmetries in (5.9).
Remark 5.4. This Lie approach led to a variant of our boundary crossing identity (15) in [Reference Muravey27] (their equation 40) up to some misprints therein. In particular, by setting
![]() $\beta^{\prime} = \beta/2k \alpha$
,
$\beta^{\prime} = \beta/2k \alpha$
,
![]() $\alpha^{\prime} = 1/\alpha^2 - \beta/2k \alpha -1$
,
$\alpha^{\prime} = 1/\alpha^2 - \beta/2k \alpha -1$
,
![]() $A=k^2$
,
$A=k^2$
,
![]() $B=0$
,
$B=0$
,
![]() $\nu=0$
,
$\nu=0$
,
![]() $x_0=0$
, and
$x_0=0$
, and
![]() $\theta_{\mathcal{F}_2}(x)= {\mathrm{e}}^{-kx^2/2}$
, we noted that the first term in (40) should be
$\theta_{\mathcal{F}_2}(x)= {\mathrm{e}}^{-kx^2/2}$
, we noted that the first term in (40) should be
![]() $\mathcal{T}_-^{-1}\mathcal{T}_+^{-1/2}\sqrt{\alpha^{\prime}+\beta^{\prime}+1}$
instead of
$\mathcal{T}_-^{-1}\mathcal{T}_+^{-1/2}\sqrt{\alpha^{\prime}+\beta^{\prime}+1}$
instead of
![]() $\mathcal{T}_+^{-1/2}/\sqrt{\alpha^{\prime}+\beta^{\prime}+1}$
.
$\mathcal{T}_+^{-1/2}/\sqrt{\alpha^{\prime}+\beta^{\prime}+1}$
.
6. Asymptotic behaviour of the FPT densities
Here we discuss the asymptotic behaviour of the FPT distribution of
![]() $T_{k}^{S_{k}^{\alpha,\beta}f}$
and the transience of the transformed curve
$T_{k}^{S_{k}^{\alpha,\beta}f}$
and the transience of the transformed curve
![]() $S_{k}^{\alpha,\beta}f$
, that is,
$S_{k}^{\alpha,\beta}f$
, that is,
As before, we assume that our boundary
![]() $f \in \mathcal{C}^1([0, \infty), \mathbb{R}^+)$
,
$f \in \mathcal{C}^1([0, \infty), \mathbb{R}^+)$
,
![]() $f(0)\neq 0$
and only consider
$f(0)\neq 0$
and only consider
![]() $\alpha>0$
, as discussed before Section 5.1. Write
$\alpha>0$
, as discussed before Section 5.1. Write
If
![]() $\zeta_{k, \alpha, \beta} = \infty$
, from Theorem 3.1 we get the following asymptotic identity:
$\zeta_{k, \alpha, \beta} = \infty$
, from Theorem 3.1 we get the following asymptotic identity:
as
![]() $ t \to \infty$
, where
$ t \to \infty$
, where
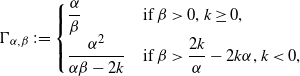 \begin{align*}\Gamma_{\alpha,\beta} \;:\!= \begin{cases}\dfrac{\alpha}{\beta} & \text{if $ \beta >0$, $ k \geq 0$,}\\\dfrac{\alpha^2}{\alpha \beta - 2 k} &\text{if $ \beta> \dfrac{2k}{\alpha} - 2k \alpha$, $ k<0$,}\end{cases}\end{align*}
\begin{align*}\Gamma_{\alpha,\beta} \;:\!= \begin{cases}\dfrac{\alpha}{\beta} & \text{if $ \beta >0$, $ k \geq 0$,}\\\dfrac{\alpha^2}{\alpha \beta - 2 k} &\text{if $ \beta> \dfrac{2k}{\alpha} - 2k \alpha$, $ k<0$,}\end{cases}\end{align*}
and
![]() $h(t) \sim I(t)$
as
$h(t) \sim I(t)$
as
![]() $t \to \zeta$
denotes that
$t \to \zeta$
denotes that
![]() $h(t)/I(t) \to 1$
as
$h(t)/I(t) \to 1$
as
![]() $t \to \zeta$
, for some
$t \to \zeta$
, for some
![]() $\zeta \in [0,\infty]$
. We now give a necessary and sufficient condition for a curve to be transient for the OU process.
$\zeta \in [0,\infty]$
. We now give a necessary and sufficient condition for a curve to be transient for the OU process.
Theorem 6.1.
![]() $S_{k}^{\alpha, \beta}f$
is transient in the following two cases:
$S_{k}^{\alpha, \beta}f$
is transient in the following two cases:
(i)
![]() $\zeta_{k, \alpha,\beta}<\infty$
;
$\zeta_{k, \alpha,\beta}<\infty$
;
(ii)
![]() $\zeta_{k, \alpha,\beta}=+ \infty$
and
$\zeta_{k, \alpha,\beta}=+ \infty$
and
Proof. In case (i), there is always a positive probability of the OU process never hitting the curves, making them transient. We now proceed with proving the result for case (ii). By relation (5.1), we deduce that
Now, by the classical Kolmogorov–Erdős–Petrovski theorem reported in [Reference Erdős18], if
![]() $t^{-1/2} \Lambda_{k} f(t)$
(i.e.
$t^{-1/2} \Lambda_{k} f(t)$
(i.e.
![]() $f(t) \,{\mathrm{e}}^{kt}/\sqrt{r(t)}$
) is increasing for sufficiently large t, then
$f(t) \,{\mathrm{e}}^{kt}/\sqrt{r(t)}$
) is increasing for sufficiently large t, then
![]() $\Lambda_{k} f$
is a transient curve for the Brownian motion if and only if
$\Lambda_{k} f$
is a transient curve for the Brownian motion if and only if
Since
![]() $\zeta_{k, \alpha, \beta}= + \infty$
, note that
$\zeta_{k, \alpha, \beta}= + \infty$
, note that
Furthermore, because of (6.2),
![]() $S_{k}^{\alpha,\beta}f(t) \,{\mathrm{e}}^{kt}/\sqrt{r(t)}$
is increasing for sufficiently large t, and under the condition
$S_{k}^{\alpha,\beta}f(t) \,{\mathrm{e}}^{kt}/\sqrt{r(t)}$
is increasing for sufficiently large t, and under the condition
we have
 \begin{align*}\int_{s(1)}^{\infty} \dfrac{{\mathrm{e}}^{3kt}S_{k}^{\alpha,\beta}f(t)}{r(t)^{3/2}} \,{\mathrm{e}}^{- {\mathrm{e}}^{2kt} \bigl(S_{k}^{\alpha,\beta}f(t)\bigr)^2/2r(t)} \,{\mathrm{d}} t &= \int_{1}^{\infty} \dfrac{1}{\sqrt{z}} g(s(z)) \,{\mathrm{e}}^{- g(s(z))^2 z/2} \,{\mathrm{d}} z \\ &< \int_{1}^{\infty} g(s(z)) \,{\mathrm{e}}^{- g(s(z))^2 z/2} \,{\mathrm{d}} z \\ &< \infty.\end{align*}
\begin{align*}\int_{s(1)}^{\infty} \dfrac{{\mathrm{e}}^{3kt}S_{k}^{\alpha,\beta}f(t)}{r(t)^{3/2}} \,{\mathrm{e}}^{- {\mathrm{e}}^{2kt} \bigl(S_{k}^{\alpha,\beta}f(t)\bigr)^2/2r(t)} \,{\mathrm{d}} t &= \int_{1}^{\infty} \dfrac{1}{\sqrt{z}} g(s(z)) \,{\mathrm{e}}^{- g(s(z))^2 z/2} \,{\mathrm{d}} z \\ &< \int_{1}^{\infty} g(s(z)) \,{\mathrm{e}}^{- g(s(z))^2 z/2} \,{\mathrm{d}} z \\ &< \infty.\end{align*}
The last integral is finite because g eventually stabilises and the assumptions ensure that g never blows up or vanishes, so its minimum and the maximum are always attained. Hence, by the integral test (6.1),
![]() $S_{k}^{\alpha,\beta}f$
is transient.
$S_{k}^{\alpha,\beta}f$
is transient.
Now we derive asymptotics for when
![]() $\zeta_{k, \alpha, \beta} < \infty$
. Notice that in this case
$\zeta_{k, \alpha, \beta} < \infty$
. Notice that in this case
and whenever f is transient and satisfies suitable conditions, we can derive the asymptotic expression of the FPT density of the OU hitting curves
![]() $S_{k}^{\alpha, \beta}f$
by making use of the corresponding result for the BM by Anderson and Pitt [Reference Anderson and Pitt4], as proved in the following proposition.
$S_{k}^{\alpha, \beta}f$
by making use of the corresponding result for the BM by Anderson and Pitt [Reference Anderson and Pitt4], as proved in the following proposition.
Proposition 6.1. Assume that f is transient and satisfies the following conditions.
-
(i)
 $\Lambda_{k} f$
is increasing, concave, twice differentiable on
$\Lambda_{k} f$
is increasing, concave, twice differentiable on
 $(0,\infty)$
and of regular variation at
$(0,\infty)$
and of regular variation at
 $\infty$
with index
$\infty$
with index
 ${a} \in [1/2,1)$
.
${a} \in [1/2,1)$
. -
(ii)
 $\Lambda_{k} f(t)/\sqrt{t}$
is increasing at
$\Lambda_{k} f(t)/\sqrt{t}$
is increasing at
 $\infty$
, and
$\infty$
, and
 $\Lambda_{k} f(t)/t$
is convex and decreases to 0 for sufficiently large t.
$\Lambda_{k} f(t)/t$
is convex and decreases to 0 for sufficiently large t. -
(iii) There exist positive constants
 $c<1$
and c’ such that the inequalities are met for sufficiently large t.
$c<1$
and c’ such that the inequalities are met for sufficiently large t. \begin{align*} t f^{\prime}(s(t)) \leq (c(2kt+1)-kt) f(s(t)), \quad | t^2/(2kt+1)^2 (f^{\prime\prime}(s(t))-k^2 f(s(t))) | \leq c^{\prime} f(s(t)) \end{align*}
\begin{align*} t f^{\prime}(s(t)) \leq (c(2kt+1)-kt) f(s(t)), \quad | t^2/(2kt+1)^2 (f^{\prime\prime}(s(t))-k^2 f(s(t))) | \leq c^{\prime} f(s(t)) \end{align*}
Then, if
![]() $\zeta_{k, \alpha, \beta} < \infty$
, we have
$\zeta_{k, \alpha, \beta} < \infty$
, we have
 \begin{align*}p_k^{S_{k}^{\alpha,\beta}f} (t) \sim \sqrt{\dfrac{|\alpha \beta|^3}{2 \pi}} \biggl(\dfrac{2k}{|\alpha \beta|} + 1\biggr) (1-r) \tilde{f}(t) \quad \text{as $ t \to \zeta_{k, \alpha,\beta}$,}\end{align*}
\begin{align*}p_k^{S_{k}^{\alpha,\beta}f} (t) \sim \sqrt{\dfrac{|\alpha \beta|^3}{2 \pi}} \biggl(\dfrac{2k}{|\alpha \beta|} + 1\biggr) (1-r) \tilde{f}(t) \quad \text{as $ t \to \zeta_{k, \alpha,\beta}$,}\end{align*}
where
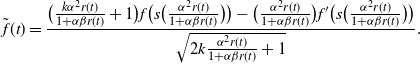 \begin{align*}\tilde{f}(t) = \dfrac{ \bigl(\frac{ k\alpha^2 r(t)}{1 + \alpha \beta r(t)}+1\bigr)f\bigl(s\bigl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \bigr)\bigr) - \bigl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)}\bigr)f^{\prime}\bigl(s\bigl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \bigr)\bigr)}{\sqrt{2k \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)}+1}}.\end{align*}
\begin{align*}\tilde{f}(t) = \dfrac{ \bigl(\frac{ k\alpha^2 r(t)}{1 + \alpha \beta r(t)}+1\bigr)f\bigl(s\bigl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \bigr)\bigr) - \bigl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)}\bigr)f^{\prime}\bigl(s\bigl( \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \bigr)\bigr)}{\sqrt{2k \frac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)}+1}}.\end{align*}
Proof. By Theorem 1 of [Reference Anderson and Pitt4], if conditions (i)–(iii) are satisfied, we can write
Using (5.1), we get
![]() $p_k^f(t) = {\mathrm{e}}^{2kt} p^{\Lambda_{k} f} (r(t))$
. We then simplify the expression and combine it with (3.1). The result follows by noticing that the assumption
$p_k^f(t) = {\mathrm{e}}^{2kt} p^{\Lambda_{k} f} (r(t))$
. We then simplify the expression and combine it with (3.1). The result follows by noticing that the assumption
![]() $\Lambda_{k} f(t)/t \downarrow 0$
as
$\Lambda_{k} f(t)/t \downarrow 0$
as
![]() $t \to \infty$
forces the exponential terms to vanish.
$t \to \infty$
forces the exponential terms to vanish.
Remark 6.1. We noted a misprint in Section 4.3 of [Reference Alili and Patie1]. For the Brownian motion, when
![]() $\beta>0$
, the one parameter family of transformed functions
$\beta>0$
, the one parameter family of transformed functions
![]() $S^{1, \beta}f$
is always transient whenever
$S^{1, \beta}f$
is always transient whenever
![]() $t^{-1/2} S^{1, \beta}f$
is increasing for sufficiently large t,
$t^{-1/2} S^{1, \beta}f$
is increasing for sufficiently large t,
![]() $0< \beta f(\alpha/\beta)< \infty$
and
$0< \beta f(\alpha/\beta)< \infty$
and
![]() $f(0)>0$
.
$f(0)>0$
.
7. Interpretation via the method of images
In [Reference Lerche25], the author did a thorough investigation of the method of images for the standard BM. Here we apply the method of images to the OU process and use it to produce new examples of curves with explicit FPT densities. As in the BM case, we would like to construct a function
![]() $h_k$
satisfying the OU Fokker–Planck equation. Then, by the uniqueness of such solutions, as seen in Section 5.3,
$h_k$
satisfying the OU Fokker–Planck equation. Then, by the uniqueness of such solutions, as seen in Section 5.3,
![]() $h_k$
would also satisfy (5.6) and be the solution to
$h_k$
would also satisfy (5.6) and be the solution to
![]() $\mathcal{H}_{k}(f)$
. We proceed as follows. First, we assume that we have a positive
$\mathcal{H}_{k}(f)$
. We proceed as follows. First, we assume that we have a positive
![]() $\sigma$
-finite measure F with
$\sigma$
-finite measure F with
![]() $\int_{0}^{\infty} \phi(\sqrt{\epsilon \theta})F({\mathrm{d}} \theta)<\infty$
for all
$\int_{0}^{\infty} \phi(\sqrt{\epsilon \theta})F({\mathrm{d}} \theta)<\infty$
for all
![]() $\epsilon>0$
. Then, for
$\epsilon>0$
. Then, for
![]() $a>0$
, we define the
$a>0$
, we define the
![]() $h_k$
function by
$h_k$
function by
We know that
![]() $ h_{k}$
vanishes on the boundary f, and so by simplifying, we find that
$ h_{k}$
vanishes on the boundary f, and so by simplifying, we find that
![]() $ h_{k}(x,t)=0$
is equivalent to
$ h_{k}(x,t)=0$
is equivalent to
where
The following lemma gives us a characterisation of the boundaries obtained through the method of images.
Lemma 7.1. (Characterisation of boundaries.) The boundaries f obtained through the method of images have the following properties:
-
(1) f is infinitely often continuously differentiable;
-
(2)
 $\Lambda_{k} f(t)/t$
(i.e.
$\Lambda_{k} f(t)/t$
(i.e.
 $f(t) \,{\mathrm{e}}^{kt}/r(t)$
) is monotone decreasing;
$f(t) \,{\mathrm{e}}^{kt}/r(t)$
) is monotone decreasing; -
(3)
 $f^{\prime\prime}(t) - k^2 f(t) \leq 0$
.
$f^{\prime\prime}(t) - k^2 f(t) \leq 0$
.
Proof. In Lemma 1.1 of [Reference Lerche25], it is shown that the curves
![]() $\eta(t)$
that satisfy the equation
$\eta(t)$
that satisfy the equation
are infinitely continuously differentiable and concave, with
![]() $\eta(t)/t$
monotone decreasing. As in our case we have
$\eta(t)/t$
monotone decreasing. As in our case we have
by changing
![]() $t \to s(t)$
, we get
$t \to s(t)$
, we get
So
![]() $\eta(t) \;:\!= \Lambda_{k} f(t)$
must satisfy the three properties given in Lemma 1.1 of [Reference Lerche25], so (1) and (2) follow directly. For (3),
$\eta(t) \;:\!= \Lambda_{k} f(t)$
must satisfy the three properties given in Lemma 1.1 of [Reference Lerche25], so (1) and (2) follow directly. For (3),
and the result follows as
![]() $\eta(t)$
is concave.
$\eta(t)$
is concave.
Remark 7.1. From Lemma 4.1, if
![]() $\mu(s(\tau f)) > k^2$
and
$\mu(s(\tau f)) > k^2$
and
![]() $f\geq 0$
, then we find that the solutions to nonlinear ordinary differential equations (4.2) satisfy
$f\geq 0$
, then we find that the solutions to nonlinear ordinary differential equations (4.2) satisfy
![]() $f^{\prime\prime} - k^2 f \leq 0$
.
$f^{\prime\prime} - k^2 f \leq 0$
.
The following theorem gives us a way of calculating the density of
![]() $T_{k}^f$
explicitly.
$T_{k}^f$
explicitly.
Theorem 7.1. The FPT density of
![]() $T_{k}^f$
is given by
$T_{k}^f$
is given by
where
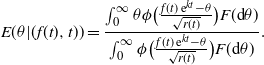 \begin{align*} E(\theta | (f(t),t)) = \dfrac{\int_{0}^{\infty} \theta \phi\bigl(\frac{f(t)\,{\mathrm{e}}^{kt} - \theta}{\sqrt{r(t)}}\bigr) F({\mathrm{d}} \theta)}{\int_{0}^{\infty} \phi\bigl(\frac{f(t)\,{\mathrm{e}}^{kt} - \theta}{\sqrt{r(t)}}\bigr) F({\mathrm{d}} \theta)}.\end{align*}
\begin{align*} E(\theta | (f(t),t)) = \dfrac{\int_{0}^{\infty} \theta \phi\bigl(\frac{f(t)\,{\mathrm{e}}^{kt} - \theta}{\sqrt{r(t)}}\bigr) F({\mathrm{d}} \theta)}{\int_{0}^{\infty} \phi\bigl(\frac{f(t)\,{\mathrm{e}}^{kt} - \theta}{\sqrt{r(t)}}\bigr) F({\mathrm{d}} \theta)}.\end{align*}
Proof. We just use relation (5.10) to get the result.
We now consider some examples of the boundaries that arise for specific measures F via Theorem 7.1.
Example 7.1. Consider
![]() $F({\mathrm{d}} \theta) = \delta_{2z}$
for some
$F({\mathrm{d}} \theta) = \delta_{2z}$
for some
![]() $z>0$
. Using
$z>0$
. Using
![]() $h_k(f(t),t)=0$
and simplifying, we get
$h_k(f(t),t)=0$
and simplifying, we get
By Theorem 7.1,
Remark 7.2. In [Reference Buonocore, Nobile and Ricciardi13], the FPT of a mean-reverting OU with parameter
![]() $\mu$
hitting a hyperbolic type boundary of the form
$\mu$
hitting a hyperbolic type boundary of the form
![]() $\mu + A \,{\mathrm{e}}^{kt} + B \,{\mathrm{e}}^{-kt}$
is studied. This reduces to the FPT of a standard OU hitting a curve of the form
$\mu + A \,{\mathrm{e}}^{kt} + B \,{\mathrm{e}}^{-kt}$
is studied. This reduces to the FPT of a standard OU hitting a curve of the form
![]() $A \,{\mathrm{e}}^{kt} + B \,{\mathrm{e}}^{-kt}$
for arbitrary constants A and B which is the curve given in this example. Also, applying the
$A \,{\mathrm{e}}^{kt} + B \,{\mathrm{e}}^{-kt}$
for arbitrary constants A and B which is the curve given in this example. Also, applying the
![]() $S_{k}$
transformation to these curves gives the same family of curves with different constant coefficients.
$S_{k}$
transformation to these curves gives the same family of curves with different constant coefficients.
If the support of the measure F is on
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $F(\{0\})=0$
, then we define
$F(\{0\})=0$
, then we define
Then there exist positive- and negative-valued functions
![]() $f_{+}$
and
$f_{+}$
and
![]() $f_{-}$
, with
$f_{-}$
, with
![]() $f_{-} < f_{+}$
and the properties
$f_{-} < f_{+}$
and the properties
![]() $ h_{k}(f_{+}(t),t)=0$
and
$ h_{k}(f_{+}(t),t)=0$
and
![]() $ h_{k}(f_{-}(t),t)=0$
for all
$ h_{k}(f_{-}(t),t)=0$
for all
![]() $t < t_a$
for a certain
$t < t_a$
for a certain
![]() $t_a \leq \infty$
. Then the stopping time can also be defined as the first exit time from the region
$t_a \leq \infty$
. Then the stopping time can also be defined as the first exit time from the region
![]() $(f_{-}(t), f_{+}(t)) $
, that is,
$(f_{-}(t), f_{+}(t)) $
, that is,
Moreover, if F is symmetric, then
![]() $f_+=-f_-$
, and the FPT distribution of
$f_+=-f_-$
, and the FPT distribution of
![]() $T_{k}^{S_{k}^{\alpha,\beta}f_\pm}$
can be obtained using our main identity (3.1) in Theorem 3.1, replacing
$T_{k}^{S_{k}^{\alpha,\beta}f_\pm}$
can be obtained using our main identity (3.1) in Theorem 3.1, replacing
![]() $T_{k}^f$
and
$T_{k}^f$
and
![]() $T_{k}^{S_{k}^{\alpha,\beta}f}$
with
$T_{k}^{S_{k}^{\alpha,\beta}f}$
with
![]() $T_{k}^{f_\pm}$
and
$T_{k}^{f_\pm}$
and
![]() $T_{k}^{S_{k}^{\alpha,\beta}f_\pm}$
, respectively. This follows directly by replacing the processes B and U with
$T_{k}^{S_{k}^{\alpha,\beta}f_\pm}$
, respectively. This follows directly by replacing the processes B and U with
![]() $|B|$
and
$|B|$
and
![]() $|U|$
, respectively. We now see an example of this.
$|U|$
, respectively. We now see an example of this.
Example 7.2. Consider
![]() $F({\mathrm{d}} \theta) = {{ {\mathrm{d}} \theta}/{\sqrt{2 \pi}}}$
on
$F({\mathrm{d}} \theta) = {{ {\mathrm{d}} \theta}/{\sqrt{2 \pi}}}$
on
![]() $\mathbb{R}$
. Then
$\mathbb{R}$
. Then
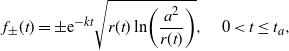 \begin{align*} f_{\pm}(t)= \pm {\mathrm{e}}^{-kt} \sqrt{r(t) \ln\biggl(\dfrac{a^2}{r(t)}\biggr)}, \quad 0<t \leq t_a, \end{align*}
\begin{align*} f_{\pm}(t)= \pm {\mathrm{e}}^{-kt} \sqrt{r(t) \ln\biggl(\dfrac{a^2}{r(t)}\biggr)}, \quad 0<t \leq t_a, \end{align*}
where
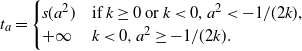 \begin{align*}t_a= \begin{cases}s(a^2) & \text{if $ k\geq0$ or $ k<0$, $a^2<-1/(2k)$,} \\ + \infty & k<0, a^2\geq -1/(2k).\end{cases}\end{align*}
\begin{align*}t_a= \begin{cases}s(a^2) & \text{if $ k\geq0$ or $ k<0$, $a^2<-1/(2k)$,} \\ + \infty & k<0, a^2\geq -1/(2k).\end{cases}\end{align*}
This is a two-sided boundary, with exit time
![]() $T_{k}^{f_{\pm}}$
defined in (7.2) and FPT density given by
$T_{k}^{f_{\pm}}$
defined in (7.2) and FPT density given by
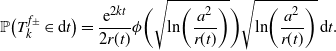 \begin{align*} \mathbb{P}\bigl(T_{k}^{f_\pm} \in {\mathrm{d}} t\bigr)= \dfrac{ {\mathrm{e}}^{2kt} }{2 r(t)} \phi\biggl( \sqrt{\ln\biggl(\dfrac{a^2 }{r(t)}\biggr)} \biggr) \sqrt{\ln\biggl(\dfrac{a^2 }{r(t)}\biggr)} \,{\mathrm{d}} t.\end{align*}
\begin{align*} \mathbb{P}\bigl(T_{k}^{f_\pm} \in {\mathrm{d}} t\bigr)= \dfrac{ {\mathrm{e}}^{2kt} }{2 r(t)} \phi\biggl( \sqrt{\ln\biggl(\dfrac{a^2 }{r(t)}\biggr)} \biggr) \sqrt{\ln\biggl(\dfrac{a^2 }{r(t)}\biggr)} \,{\mathrm{d}} t.\end{align*}
Applying the
![]() $S_{k}$
transformation (1.2) to this curve, we get
$S_{k}$
transformation (1.2) to this curve, we get
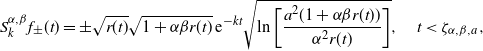 \begin{equation} S_{k}^{\alpha,\beta} f_{\pm}(t) = \pm \sqrt{r(t)} \sqrt{1+ \alpha \beta r(t)} \,{\mathrm{e}}^{-kt} \sqrt{\ln{\biggl[\dfrac{a^2 (1 + \alpha \beta r(t)) }{ \alpha^2 r(t)} \biggr]}}, \quad t< \zeta_{\alpha,\beta,a},\end{equation}
\begin{equation} S_{k}^{\alpha,\beta} f_{\pm}(t) = \pm \sqrt{r(t)} \sqrt{1+ \alpha \beta r(t)} \,{\mathrm{e}}^{-kt} \sqrt{\ln{\biggl[\dfrac{a^2 (1 + \alpha \beta r(t)) }{ \alpha^2 r(t)} \biggr]}}, \quad t< \zeta_{\alpha,\beta,a},\end{equation}
where
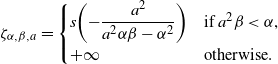 \begin{align*} \zeta_{\alpha, \beta, a} = \begin{cases}s\biggl({-} \dfrac{a^2}{a^2 \alpha \beta - \alpha^2}\biggr) & \text{if $ a^2 \beta < \alpha$,}\\ + \infty & \text{otherwise.}\end{cases}\end{align*}
\begin{align*} \zeta_{\alpha, \beta, a} = \begin{cases}s\biggl({-} \dfrac{a^2}{a^2 \alpha \beta - \alpha^2}\biggr) & \text{if $ a^2 \beta < \alpha$,}\\ + \infty & \text{otherwise.}\end{cases}\end{align*}
The FPT density is given by
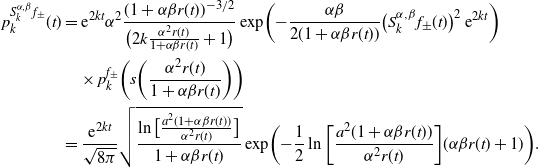 \begin{align*} p_k^{S_{k}^{\alpha,\beta} f_{\pm}}(t) & = {\mathrm{e}}^{2kt} \alpha^2 \dfrac{(1+ \alpha \beta r(t))^{-3/2}}{\bigl(2k \frac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \bigr)} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl( S_{k}^{\alpha,\beta} f_{\pm}(t)\bigr)^2 \,{\mathrm{e}}^{2kt}} \biggr) \\ &\quad\times p_k^{f_{\pm}}\biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \\ & = \dfrac{{\mathrm{e}}^{2kt}}{\sqrt{8 \pi}} \sqrt{\dfrac{\ln{\bigl[\frac{a^2 (1 + \alpha \beta r(t)) }{ \alpha^2 r(t)} \bigr]}}{1+ \alpha \beta r(t)}} \,\mathrm{{exp}}\biggl({ - \frac{1}{2} \ln{\biggl[\frac{a^2 (1+\alpha \beta r(t)) }{ \alpha^2 r(t)} \biggr]} (\alpha \beta r(t) +1)}\biggr) .\end{align*}
\begin{align*} p_k^{S_{k}^{\alpha,\beta} f_{\pm}}(t) & = {\mathrm{e}}^{2kt} \alpha^2 \dfrac{(1+ \alpha \beta r(t))^{-3/2}}{\bigl(2k \frac{\alpha^2 r(t)}{1+ \alpha \beta r(t)} + 1 \bigr)} \,\mathrm{{exp}}\biggl({- \frac{\alpha \beta }{2(1 + \alpha \beta r(t))} \bigl( S_{k}^{\alpha,\beta} f_{\pm}(t)\bigr)^2 \,{\mathrm{e}}^{2kt}} \biggr) \\ &\quad\times p_k^{f_{\pm}}\biggl(s\biggl( \dfrac{ \alpha^2 r(t)}{1 + \alpha \beta r(t)} \biggr) \biggr) \\ & = \dfrac{{\mathrm{e}}^{2kt}}{\sqrt{8 \pi}} \sqrt{\dfrac{\ln{\bigl[\frac{a^2 (1 + \alpha \beta r(t)) }{ \alpha^2 r(t)} \bigr]}}{1+ \alpha \beta r(t)}} \,\mathrm{{exp}}\biggl({ - \frac{1}{2} \ln{\biggl[\frac{a^2 (1+\alpha \beta r(t)) }{ \alpha^2 r(t)} \biggr]} (\alpha \beta r(t) +1)}\biggr) .\end{align*}
Now, for example, by setting
![]() $a=1, \alpha=2, \beta=k$
, we get
$a=1, \alpha=2, \beta=k$
, we get
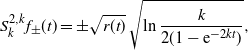 \begin{align*} S_{k}^{2,k} f_{\pm}(t) = \pm \sqrt{r(t)} \; \sqrt{\ln{\dfrac{k }{ 2 (1 - {\mathrm{e}}^{-2kt})} }},\end{align*}
\begin{align*} S_{k}^{2,k} f_{\pm}(t) = \pm \sqrt{r(t)} \; \sqrt{\ln{\dfrac{k }{ 2 (1 - {\mathrm{e}}^{-2kt})} }},\end{align*}
with FPT density given by
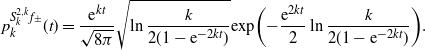 \begin{align*} p_k^{ S_{k}^{2,k} f_{\pm}}(t) = \dfrac{{\mathrm{e}}^{kt}}{\sqrt{8 \pi}} \sqrt{\ln{\dfrac{k }{ 2 (1 - {\mathrm{e}}^{-2kt})} }} \mathrm{{exp}}\biggl({ - \frac{{\mathrm{e}}^{2kt}}{2}\ln{\frac{k }{ 2 (1 - {\mathrm{e}}^{-2kt})} }}\biggr).\end{align*}
\begin{align*} p_k^{ S_{k}^{2,k} f_{\pm}}(t) = \dfrac{{\mathrm{e}}^{kt}}{\sqrt{8 \pi}} \sqrt{\ln{\dfrac{k }{ 2 (1 - {\mathrm{e}}^{-2kt})} }} \mathrm{{exp}}\biggl({ - \frac{{\mathrm{e}}^{2kt}}{2}\ln{\frac{k }{ 2 (1 - {\mathrm{e}}^{-2kt})} }}\biggr).\end{align*}
In Figure 3 we display the transformed curves (7.3) for different values of
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
. In particular, for
$\beta$
. In particular, for
![]() $a^2\beta < \alpha$
, we get closed curves defined on
$a^2\beta < \alpha$
, we get closed curves defined on
![]() $t \in (0,\zeta_{\alpha, \beta, a})$
, approaching 0 as
$t \in (0,\zeta_{\alpha, \beta, a})$
, approaching 0 as
![]() $t\to 0$
or
$t\to 0$
or
![]() $t\to \zeta_{\alpha,\beta,0}$
; see Figure 3(a). Otherwise, we get open curves that diverge to
$t\to \zeta_{\alpha,\beta,0}$
; see Figure 3(a). Otherwise, we get open curves that diverge to
![]() $\pm \infty$
; see Figure 3(b).
$\pm \infty$
; see Figure 3(b).
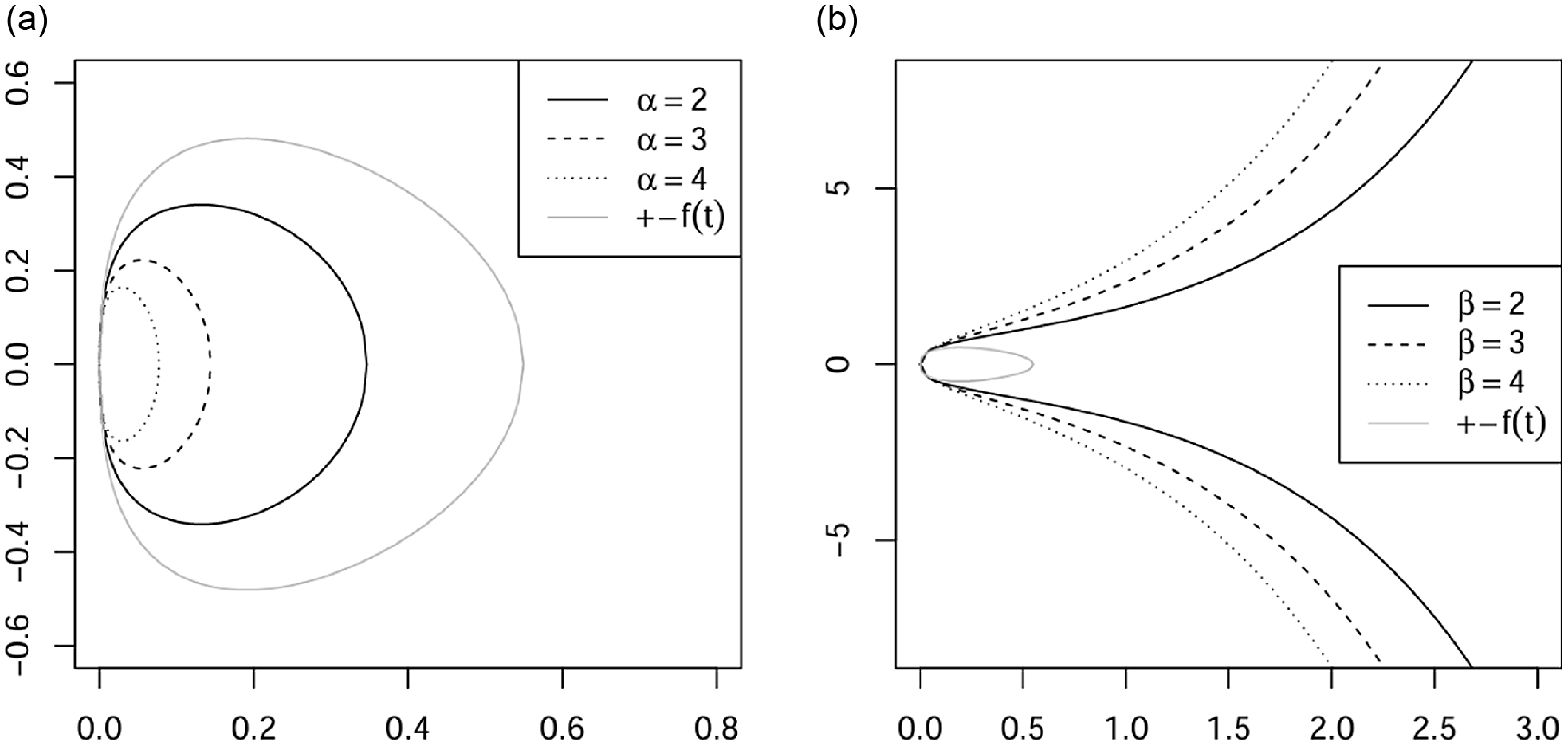
Figure 3. Transformed curves (7.3) when
![]() $a^2\beta < \alpha$
(a) and
$a^2\beta < \alpha$
(a) and
![]() $a^2\beta > \alpha$
(b). In particular, we choose
$a^2\beta > \alpha$
(b). In particular, we choose
![]() $\beta=1, k=1, a=1$
with
$\beta=1, k=1, a=1$
with
![]() $\alpha= 2,3,4$
in (a), and
$\alpha= 2,3,4$
in (a), and
![]() $k=1, a=1, \alpha = 1$
and
$k=1, a=1, \alpha = 1$
and
![]() $\beta=2,3,4$
in (b).
$\beta=2,3,4$
in (b).
Remark 7.3. Back to our
![]() $S_{k}^{\alpha,\beta}$
transformation, using (7.1) with the time-transformation
$S_{k}^{\alpha,\beta}$
transformation, using (7.1) with the time-transformation
we get
where
is the measure corresponding to the curve
![]() $S_{k}^{\alpha,\beta} f(t)$
, for
$S_{k}^{\alpha,\beta} f(t)$
, for
![]() $t<\zeta_{k, \alpha,\beta}$
.
$t<\zeta_{k, \alpha,\beta}$
.
Acknowledgements
We are grateful to Dmitry Muravey for a discussion on the Lie symmetries while finalising the paper, and the anonymous referees for their comments. For the purpose of open access, the authors have applied a Creative Commons Attribution (CC BY) licence to any Author Accepted Manuscript version arising from this submission.
Funding information
AA was funded by EPSRC grant [EP/V520226/1] as part of the Warwick CDT in Mathematics and Statistics.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.

























