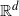 $\mathbb{R}^{d}$
$\mathbb{R}^{d}$Published online by Cambridge University Press: 28 October 2022
We study Bose gases in
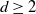 $d \ge 2$
dimensions with short-range repulsive pair interactions at positive temperature, in the canonical ensemble and in the thermodynamic limit. We assume the presence of hard Poissonian obstacles and focus on the non-percolation regime. For sufficiently strong interparticle interactions, we show that almost surely there cannot be Bose–Einstein condensation into a sufficiently localized, normalized one-particle state. The results apply to the canonical eigenstates of the underlying one-particle Hamiltonian.
$d \ge 2$
dimensions with short-range repulsive pair interactions at positive temperature, in the canonical ensemble and in the thermodynamic limit. We assume the presence of hard Poissonian obstacles and focus on the non-percolation regime. For sufficiently strong interparticle interactions, we show that almost surely there cannot be Bose–Einstein condensation into a sufficiently localized, normalized one-particle state. The results apply to the canonical eigenstates of the underlying one-particle Hamiltonian.