Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T05:48:52.043Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotics of conditional moments of the summand in Poisson compounds

Part of: Operations research and management science Distribution theory

Published online by Cambridge University Press:  14 July 2016

Tomasz Rolski  and
Agata Tomanek
Tomasz Rolski
Affiliation:
University of Wrocław, Mathematical Institute, University of Wrocław, pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland. Email address: [email protected]
Agata Tomanek
Affiliation:
University of Wrocław, Mathematical Institute, University of Wrocław, pl. Grunwaldzki 2/4, 50-384 Wrocław, Poland. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose that N is a ℤ+-valued random variable and that X,X1,X2,… is a sequence of independent and identically distributed ℤ+ random variables independent of N. In this paper we are interested in properties of the conditional variable 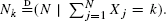In particular, we want to know the asymptotic behavior of the conditional mean ENk or the conditional variance varNk as k→∞. We consider the cases when X is Poisson and when X is mixed Poisson. The problem is motivated by modeling loss reserves in nonlife insurance.

Keywords

Compound Poissonconditional expectationloss reserving

MSC classification

Primary: 62E20: Asymptotic distribution theory
Secondary: 90B30: Production models
Type
Part 1. Risk Theory
Information
Journal of Applied Probability , Volume 48 , Issue A: New Frontiers in Applied Probability (Journal of Applied Probability Special Volume 48A) , August 2011 , pp. 65 - 76
Copyright
Copyright © Applied Probability Trust 2011 

References

[1] Billinglsey, P., (1986). Probability and Measure, 2nd edn. John Wiley, New York.Google Scholar
[2] De Bruijn, N. G., (1981). Asymptotic Methods in Analysis. Dover, New York.Google Scholar
[3] Harper, L. H., (1967). Stirling behavior is asymptotically normal. Ann. Math. Statist. 38, 410–414.Google Scholar
[4] Jessen, A. H., Mikosch, T. and Samorodnitsky, G., (2010). Prediction of outstanding payments in a Poisson cluster. Scand. Actuarial J. 2010, 1651–2030.Google Scholar
[5] Lovász, L., (2007). Combinatorial Problems and Exercises. Corrected republication of the 1993 edition. AMS Chelsea, Providence, RI.Google Scholar
[6] Matsui, M. and Mikosch, T., (2010). Prediction in a Poisson cluster model. J. Appl. Prob. 47, 350–366.Google Scholar
[7] Norberg, R., (1993). Prediction of outstanding liabilities in non-life insurance. ASTIN Bull. 23, 95–115.Google Scholar
[8] Norberg, R., (1999). Prediction of outstanding liabilities II. Model variations and extensions. ASTIN Bull. 29, 5–25.Google Scholar
[9] Pitman, J., (1997). Some probabilistic aspects of set partitions. Amer. Math. Monthly 104, 201–209.Google Scholar
[10] Rényi, A., (1970). Probability Theory. North-Holland, Amsterdam.Google Scholar