Published online by Cambridge University Press: 16 July 2020
A uniform recursive tree on n vertices is a random tree where each possible 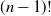 $(n-1)!$
labelled recursive rooted tree is selected with equal probability. We introduce and study weighted trees, a non-uniform recursive tree model departing from the recently introduced Hoppe trees. This class generalizes both uniform recursive trees and Hoppe trees, providing diversity among the nodes and making the model more flexible for applications. We analyse the number of leaves, the height, the depth, the number of branches, and the size of the largest branch in these weighted trees.
$(n-1)!$
labelled recursive rooted tree is selected with equal probability. We introduce and study weighted trees, a non-uniform recursive tree model departing from the recently introduced Hoppe trees. This class generalizes both uniform recursive trees and Hoppe trees, providing diversity among the nodes and making the model more flexible for applications. We analyse the number of leaves, the height, the depth, the number of branches, and the size of the largest branch in these weighted trees.