Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Voit, Michael
1997.
Rate of convergence to Gaussian measures on $n$-spheres and Jacobi hypergroups.
The Annals of Probability,
Vol. 25,
Issue. 1,
Kotz, Samuel
and
Balakrishnan, N.
1997.
Advances in Combinatorial Methods and Applications to Probability and Statistics.
p.
203.
Voit, Michael
1998.
Asymptotics of Heat Kernels on Projective Spaces of Large Dimensions and on Disk Hypergroups.
Mathematische Nachrichten,
Vol. 194,
Issue. 1,
p.
225.
Voit, Michael
2000.
A note on the rate of convergence to equilibrium for Erlang's model in the subcritical case.
Journal of Applied Probability,
Vol. 37,
Issue. 03,
p.
918.
Voit, Michael
2000.
A note on the rate of convergence to equilibrium for Erlang's model in the subcritical case.
Journal of Applied Probability,
Vol. 37,
Issue. 3,
p.
918.
Feinsilver, Philip
and
Kocik, Jerzy
2005.
Recent Advances in Applied Probability.
p.
115.
Ceccherini-Silberstein, T.
Scarabotti, F.
and
Tolli, F.
2007.
Finite Gel’fand pairs and their applications to probability and statistics.
Journal of Mathematical Sciences,
Vol. 141,
Issue. 2,
p.
1182.
Gayrard, Véronique
and
Ben Arous, Gérard
2008.
Elementary potential theory on the hypercube..
Electronic Journal of Probability,
Vol. 13,
Issue. none,
Kaplun, A.
2010.
The Continuous-Time Ehrenfest Process in Term Structure Modelling.
Journal of Applied Probability,
Vol. 47,
Issue. 03,
p.
693.
Makmal, Adi
Tiersch, Markus
Ganahl, Clemens
and
Briegel, Hans J.
2016.
Quantum walks on embedded hypercubes: Nonsymmetric and nonlocal cases.
Physical Review A,
Vol. 93,
Issue. 2,
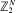 in continuous time t
in continuous time t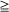 0 can be expressed in terms of binomial distributions; their limit behaviour for t, N → ∞ is well-known. We study here these random walks in discrete time and derive explicit bounds for the deviation of their distribution from their counterparts in continuous time with respect to the total variation norm. Our results lead to a recent asymptotic result of Diaconis, Graham and Morrison for the deviation from uniformity for N →∞. Our proofs use Krawtchouk polynomials and a version of the Diaconis–Shahshahani upper bound lemma. We also apply our methods to certain birth-and-death random walks associated with Krawtchouk polynomials.
0 can be expressed in terms of binomial distributions; their limit behaviour for t, N → ∞ is well-known. We study here these random walks in discrete time and derive explicit bounds for the deviation of their distribution from their counterparts in continuous time with respect to the total variation norm. Our results lead to a recent asymptotic result of Diaconis, Graham and Morrison for the deviation from uniformity for N →∞. Our proofs use Krawtchouk polynomials and a version of the Diaconis–Shahshahani upper bound lemma. We also apply our methods to certain birth-and-death random walks associated with Krawtchouk polynomials.