Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T10:58:38.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic behaviour of population-size-dependent branching processes in Markovian random environments

Part of: Markov processes

Published online by Cambridge University Press:  14 July 2016

Han-Xing Wang  and
Dafan Fang
Han-Xing Wang*
Affiliation:
Shanghai University
Dafan Fang*
Affiliation:
Yueyang Normal College
*
∗Postal address: Department of Mathematics, Shanghai University, Shanghai 201800, P.R. China.
∗∗Postal address: Department of Mathematics, Yueyang Normal College, Yueyang 414000, P.R. China.
Get access Rights & Permissions [Opens in a new window]

Abstract

A population-size-dependent branching process {Zn} is considered where the population's evolution is controlled by a Markovian environment process {ξn}. For this model, let mk,θ and 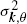be the mean and the variance respectively of the offspring distribution when the population size is k and a environment θ is given. Let B = {ω : Zn(ω) = 0 for some n} and q = P(B). The asymptotic behaviour of limnZn and 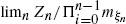is studied in the case where supθ|mk,θ − mθ| → 0 for some real numbers {mθ} such that infθmθ > 1. When the environmental sequence {ξn} is a irreducible positive recurrent Markov chain (particularly, when its state space is finite), certain extinction (q = 1) and non-certain extinction (q < 1) are studied.

Keywords

Markov chains in random environmentsbranching modelsextinction probabilities

MSC classification

Primary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Short Communications
Information
Journal of Applied Probability , Volume 36 , Issue 2 , June 1999 , pp. 611 - 619
Copyright
Copyright © Applied Probability Trust 1999 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Athreya, K. B., and Karlin, S. (1971). On branching processes with random environments. I: extinction probabilities. Ann. Math. Statist. 42, 1499–1520.CrossRefGoogle Scholar
Cogburn, R. (1980). Markov chains in random environments: the case of Markovian environments. Ann. Prob. 8, 908–916.CrossRefGoogle Scholar
Cogburn, R. (1984). The ergodic theory of Markov chains in random environments. Z. Wahrscheinlichkeitsth. 66, 109–128.CrossRefGoogle Scholar
Fujimagari, T. (1976). Controlled Galton–Watson process and its asymptotic behaviour. Kodai Math. Sem. Rep. 27, 11–18.CrossRefGoogle Scholar
Klebaner, F. C. (1984). On population-size-dependent branching process. Adv. Appl. Prob. 16, 30–55.CrossRefGoogle Scholar
Klebaner, F. C. (1984). Geometric rate of growth in population-size-dependent branching processes. J. Appl. Prob. 21, 40–49.CrossRefGoogle Scholar
Pierre Loti Viaud, D. (1994). A strong law and a central limit theorem for controlled Galton–Watson process. J. Appl. Prob. 31, 22–37.CrossRefGoogle Scholar
Wang, H.-X. (1999). Extinction of population-size-dependent branching processes in random environments. J. Appl. Prob. 36, 146–154.CrossRefGoogle Scholar